Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 8 - Chân trời sáng tạo
Đề thi giữa kì 2 Toán 8 - Đề số 7 - Chân trời sáng tạo
Đề thi giữa kì 2 Toán 8 - Đề số 8 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 6 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 5 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 4 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 3 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 2 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 1 - Chân trời sáng tạoĐề thi giữa kì 2 Toán 8 - Đề số 7 - Chân trời sáng tạo
Phần trắc nghiệm (2 điểm) Câu 1: Đường trung bình của tam giác: A. Là đoạn thẳng nối hai điểm bất kì trên hai cạnh của tam giác
Đường trung bình của tam giác:
Đáp án : B
Áp dụng định lý 2 đường trung bình của tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy
+) Đáp án AA sai vì đoạn thẳng nối 2 điểm bất kì của tam giác không thể khẳng định ngay là đường trung bình.
+) Đáp án B: Đường trung bình của tam giác là đoạn thẳng cắt hai cạnh của tam giác, song song với cạnh thứ ba và bằng nửa cạnh ấy.
Đáp án B.
Hàm số nào dưới đây không phải hàm số bậc nhất?
Đáp án : C
Hàm số bậc nhất là hàm số được cho bởi công thức y=ax+b với a,b là các số cho trước và a≠0
y=√3(x+1)=√3x+√3 là hàm số bậc nhất
y=2−3x=−3x+2 là hàm số bậc nhất
y=4x2 không là hàm số bậc nhất
y=−5x là hàm số bậc nhất
Đáp án C.
Bác An đã gửi một lượng tiền tiết kiệm kì hạn 1 năm ở một ngân hàng với lãi suất 5,6%/năm (cứ sau kì hạn 1 năm, tiền lãi của kì hạn đó lại được cộng vào tiền vốn). Sau khi gửi 2 năm, bác An có được số tiền cả gốc và lãi là 111513600 đồng. Hỏi ban đầu bác An đã gửi vào ngân hàng số tiền là bao nhiêu đồng? Biết rằng lãi suất ngân hàng không thay đổi trong 2 năm đó.
Đáp án : B
Giải bài toán bằng cách lập phương trình bậc nhất.
Gọi số tiền ban đầu bác An gửi vào ngân hàng là x (đồng). Điều kiện x∈N∗
Lãi suất của năm thứ nhất là 5,6%.x=0,056x (đồng)
Số tiền của bác An sau một năm là x+0,056x=1,056x (đồng)
Lãi suất năm thứ hai là 5,6%.1,056 =0,059136x (đồng)
Số tiền của bác An sau 2 năm:
1,056x+0,059136x=1,115136x (đồng)
Theo giả thiết, ta có phương trình:
1,115136x=111513600
x=111513600:1,115136
x=100000000(TM)
Vậy ban đầu bác An gửi vào ngân hàng 100000000 đồng.
Đáp án B.
Cho tam giác MNP có MD là tia phân giác của góc M(D∈NP). Trong các khẳng định sau, khẳng định nào đúng?
Đáp án : A
Tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề đoạn ấy.
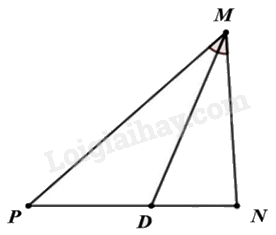
Vì MD là tia phân giác góc M(D∈NP) nên theo tính chất đường phân giác tacó: DNDP=MNMP;DNMN=DPMP;DPDN=MPMN;DPMP=DNMN
Đáp án A.
Cho các điểm A(−3;8),B(−2;−5),C(1;0) và D(12;34), điểm thuộc đồ thị của hàm số y=x2−1 là:
Đáp án : A
Thay tọa độ của mỗi điểm vào đồ thị hàm số, xem thỏa mãn hay không.
Thay tọa độ điểm A(−3;8) vào y=x2−1 ta được: 8=(−3)2−1=8 (luôn đúng)
Thay tọa độ điểm B(−2;−5) vào y=x2−1 ta được: −5=(−2)2−1=3 (vô lí)
Thay tọa độ điểm C(0;1) vào y=x2−1 ta được: 1=02−1=−1 (vô lí))
Thay tọa độ điểm D(12;34) vào y=x2−1 ta được: 34=(12)2−1=14−1=−34 (vô lí)
Đáp án A.
Cho tam giác ABC Một đường thẳng d song song với BC và cắt các cạnh AB,AC của tam giác đó lần lượt tại M,N với AMAB=13 và AN+AC=16cm. Tính AN.
Đáp án : A
Áp dụng định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Áp dụng tính chất dãy tỉ số bằng nhau.
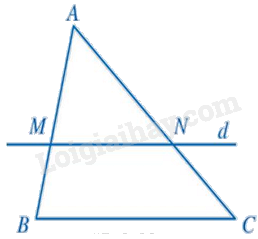
Do MN//BC nên AMAB=ANAC=13.
Do đó AN1=AC3=AN+AC1+3=164=4.
Suy ra AN=4cm.
Đáp án A.
Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân ABC(AB=AC=2m) cùng các thanh sắt nằm ngang GF,HE,ID,BC và sau đó gắn cây thông như như hình vẽ. Tính số tiền sắt cần sử dụng để làm cây thông noel đó. Biết giá một mét sắt là 55000 đồng và AG=GH=HI=IB,CD=DE=EF=FA, thanh GF dài 0,2m.
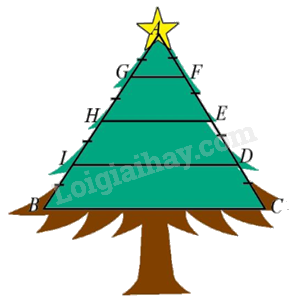
Đáp án : D
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh tam giác đó.
Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.
Áp dụng thêm: định lí Thales đảo, định lí Thales.
Vì G,F lần lượt là trung điểm của AH,AE
Suy ra GF là đường trung bình của ΔAHE suy ra HE=2GF=2.0,2=0,4(m).
Vì H,E lần lượt là trung điểm của AB,AC
Suy ra HE là đường trung bình của ΔABC suy ra BC=2HE=2.0,4=0,8(m).
Ta có AIAB=ADAC=34 nên theo định lí Thales đảo thì ID//BC suy ra IDBC=AIAB=34 (định lí Thales)
Do đó ID=34BC=34⋅0,8=0,6(m).
Số tiền cần trả để hoàn thành cây thông noel đó là: (0,2+0,4+0,6+0,8+2+2).55000=330000 (đồng).
Đáp án D.
Toà nhà Bitexco Financial (hay tháp tài chính Bitexco) được xây dựng tại trung tâm Quận 1, Thành phố Hồ Chí Minh. Toà nhà có 68 tầng (không kể các tầng hầm). Biết rằng khi toà nhà có bóng MP in trên mặt đất dài 47,5m, thì cùng thời điểm đó một cột cờ AB cao 12m có bóng AP in trên mặt đất dài 2,12m. Tính chiều cao MN của toà nhà theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
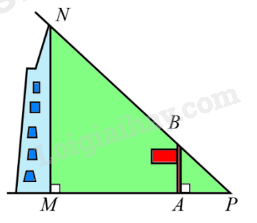
Đáp án : B
Hệ quả định lí Thales: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cąnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Ta có {NM⊥MPBA⊥MP suy ra BA∥NM
Áp dụng hệ quả định lí Thales trong ΔMNP có ABMN=APMP hay 12MN=2,1247,5 suy ra MN=12.47,52,12≈269(m)
Vậy chiều cao MN của toà nhà khoảng 269m (đã làm tròn kết quả đến hàng đơn vị)
Đáp án B.
Giải các phương trình sau:
a) 0,1x−5=0,2−x
b) 2x−53=2−x6;
c) √3x−1=x−3.
Phương trình bậc nhất ax+b=0(a≠0) có nghiệm x=−ba
Sử dụng quy tắc chuyển vế đổi dấu, quy tắc nhân hoặc chia.
a) 0,1x−5=0,2−x
0,1x+x=0,2+5
1,1x=5,2
x=5,2:1,1
x=5211
Vậy x=5211
b) 2x−53=2−x6
2(2x−5)6=2−x6
4x−10=2−x
4x+x=2+10
5x=12
x=125
Vậy x=125
c) √3x−1=x−3
√3x−x=−3+1
(√3−1)x=−2
x=−2√3−1
Vậy x=−2√3−1
Cho ba đường thẳng d1:y=−2x+5;d2:y=−2x;d3:y=4x−1. Chỉ ra các cặp đường thẳng song song, cắt nhau hoặc trùng nhau.
Cho hai đường thẳng d:y=ax+b(a≠0) và d′:y=a′x+b′(a′≠0)
Nếu a=a′;b≠b′ thì d∥d′
Nếu a=a′;b=b′ thì d trùng với d′
Nếu a≠a′ thì d và d′ cắt nhau.
Ta có d1:y=−2x+5;d2:y=−2x;d3:y=4x−1
+) {−2=−25≠0 suy ra d1 song song d2
+)−2≠4 suy ra d1 cắt d4;d2 cắt d4
Một tổ sản xuất của công ty may Đức Long được giao may một số áo sơ mi để xuất khẩu trong 20 ngày. Khi thực hiện, tổ sản xuất đó đã tăng năng suất 20% nên sau 18 ngày không những đã xong số áo đó mà còn may thêm được 24 áo nữa. Tính số áo sơ mi mà tổ đó đã may được trên thực tế.
Giải bài toán bằng cách lập phương trình bậc nhất.
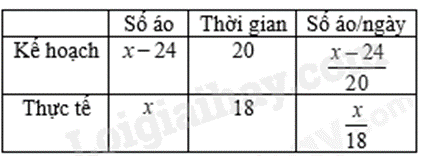
PT: Thực tế năng suất tăng 20% so với kế hoạch.
Gọi số áo sơ mi tổ đó đã may được trên thực tế là x chiếc. Điều kiện x∈N,x>24.
Trên thực tế, một ngày tổ may được x18 chiếc.
Theo kế hoạch, số áo sơ mi tổ cần may là x−24 chiếc
Theo kế hoạch, một ngày cần may được x−2420 chiếc.
Vì thực tế tăng 20% so với kế hoạch nên ta có PT:
x18=x−2420⋅120%
x18=(x−24)⋅350
25x=9.3(x−24)
25x=27x−648
27x−25x=648
2x=648
x=324(TM)
Vậy số áo sơ mi tổ đã may được trên thực tế là 324 chiếc.
Cho tam giác ABC,2 trung tuyến BM và CN cắt nhau tại G. Gọi D,E lần lượt là trung điểm GB và GC. Chứng minh rằng:
a) MN//DE
b) ND//ME
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Tính chất: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
a) Chứng minh MN∥DE vì cùng song song với BC
b) Chứng minh được MN=DE (sử dụng tính chất đường trung bình)
Chứng minh MNDE là hình bình hành suy ra điều phải chứng minh phần b.
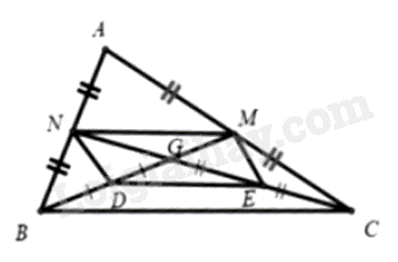
a) Vì BM,CN là 2 trung tuyến của ΔABC(GT)
Suy ra M,N lần lượt là trung điểm của AB,AC(tc)
Suy ra MN là đường trung bình ΔABC nên MN∥BC (1)
Vì D, E lần lượt là trung điểm của GB, GC(GT) nên DE là đường trung bình của ΔGBC nên DE∥BC (2)
Từ (1) và (2)⇒MN∥DE (ĐL 3 đường thẳng song song)
b) Vì MN là đường trung bình ΔABC nên MN=BC2 (tc)
Vì DE là đường trung bình của ΔGBC nên DE=BC2 (tc)
Suy ra MN=DE mà MN∥DE (theo a)
Do đó MNDE là hình bình hành (DHNB) suy ra ND∥ME(tc)
Cho hình vẽ, một người đứng ở vị trí M trên cây cầu bắc qua con kênh quan sát ba điểm thẳng hàng A,B,D lần lượt là chân hai cột đèn trồng ở bờ kênh và chân cầu. Người đó nhận thấy góc nhìn đến hai điểm A, D thì bằng góc nhìn đến hai điểm B,D, tức là ^AMD=^BMD. Người đó muốn ước lượng tỉ số khoảng cách từ vị trí M đang đứng đến điểm A và đến điểm B mà không cần phải đo trực tiếp hai khoảng cách đó. Hỏi có thể ước lượng tỉ số đó được hay không?

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Từ giả thiết ta có ^AMD=^BMD, suy ra MD là phân giác của ^AMB
Do đó MAMB=DADB.
Vậy người đó có thể ước lượng được tỉ số khoàng cách từ vị tri M đang đứng đến điểm A và đến điểm B mà không cần phải đo trực tiếp hai khoảng cách đó bằng cách đo các khoàng cách DA,DB và tính DADB.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365