Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 2 Toán 8 - Kết nối tri thức
Đề thi học kì 2 Toán 8 - Đề số 2 - Kết nối tri thức
Đề thi học kì 2 Toán 8 - Đề số 3 - Kết nối tri thức Đề thi học kì 2 Toán 8 - Đề số 4 - Kết nối tri thức Đề thi học kì 2 Toán 8 - Đề số 5 - Kết nối tri thức Đề thi học kì 2 Toán 8 - Đề số 1 - Kết nối tri thức Đề cương ôn tập học kì 2 Toán 8 - Kết nối tri thứcĐề thi học kì 2 Toán 8 - Đề số 2 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn?
Đáp án : B
Phương trình bậc nhất một ẩn có dạng ax+b=0 với a≠0.
Phương trình 3x−y=0 là phương trình bậc nhất hai ẩn.
Phương trình 2y+1=0 là phương trình bậc nhất ẩn y với a=2 nên ta chọn đáp án B.
Phương trình 4+0.x=0 có a = 0 nên không phải phương trình bậc nhất một ẩn.
Phương trình 3x2=8 là phương trình bậc hai.
Đáp án B.
Phương trình 3x+m−x−1=0 nhận x=−3 là nghiệm thì m là:
Đáp án : C
Thay x=−3 vào phương trình để tìm m.
Thay x=−3 vào phương trình 3x+m−x−1=0 ta được:
3.(−3)+m−(−3)−1=0−9+m+3−1=0m−7=0m=7
Đáp án C.
Một ô tô đi từ A đến B từ 6 giờ sáng, lúc 7 giờ sáng cùng ngày, một xe khách cũng đi từ A và tới B cùng lúc với ô tô. Vậy nếu gọi thời gian đi của xe khách là x ( giờ) thì thời gian đi của ô tô là:
Đáp án : A
Biểu diễn thời gian đi của ô tô theo x.
Vì ô tô đi từ A đến B lúc 6 giờ sáng còn xe khách đi từ A đến B lúc 7 giờ sáng và hai xe đến B cùng lúc nên thời gian ô tô đi từ A đến B là x + (7 – 6) = x + 1 (giờ)
Đáp án A.
Cho hàm số y=f(x)=2x+1, điểm nào sau đây thuộc đồ thị hàm số
Đáp án : B
Thay tọa độ của các điểm để kiểm tra xem điểm nào thuộc đồ thị hàm số.
Ta có:
f(0)=2.0+1=1≠−1 nên điểm (0,−1) không thuộc đồ thị hàm số, điểm (0;1) thuộc đồ thị hàm số.
f(2)=2.2+1=5≠1 nên điểm (2;1) không thuộc đồ thị hàm số.
f(12)=2.12+1=1+1=2≠0 nên điểm (12;0) không thuộc đồ thị hàm số.
Vậy B đúng.
Đáp án B.
Giá trị m để đường thẳng y=mx−4 cắt đường thẳng y=2x−1 tại điểm có hoành độ bằng 2 là:
Đáp án : A
Thay hoành độ x = 2 vào đường thẳng y=2x−1 để tìm giao điểm của hai đường thẳng.
Thay tọa độ điểm đó vào đường thẳng y=mx−4 để tìm m.
Tung độ giao điểm của hai đường thẳng là:
y=2.2−1=3
Suy ra giao điểm của hai đường thẳng là điểm (2;3).
Thay tọa độ giao điểm vào đường thẳng y=mx−4, ta được:
3=m.2−42m=3+42m=7m=72
Đáp án A.
Một túi đựng các viên kẹo giống hệt nhau, chỉ khác màu nhau, trong đó có 6 viên kẹo màu cam, 3 viên kẹo màu đỏ, 7 viên kẹo màu trắng. An lấy ngẫu nhiên một viên kẹo trong túi. Tính xác suất lấy được viên kẹo màu cam.
Đáp án : C
Xác định tổng số kết quả có thể và số kết quả thuận lợi cho biến cố
Tính tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể.
Có 6 + 3 + 7 = 16 kết quả có thể khi lấy ngẫu nhiên một viên kẹo trong túi.
Có 6 kết quả thuận lợi cho biến cố “lấy được viên kẹo màu cam” nên xác suất lấy được viên kẹo màu cam là:
616=38.
Đáp án C.
Một cửa hàng thống kê số lượng các loại điện thoại bán được trong một năm vừa qua như sau:

Tính xác suất thực nghiệm của biến cố E: “Chiếc điện thoại loại A được bán năm đó của của hàng”.
Đáp án : A
Tính tổng số điện thoại bán được trong năm của cửa hàng.
Tính xác suất thực nghiệm của biến cố.
Tổng số điện thoại bán được trong năm của cửa hàng:
715+1035+1085=2835
Xác suất thực nghiệm của biến cố E: “Chiếc điện thoại loại A được bán năm đó của của hàng” là:
7152835=143567
Đáp án A.
Cho tam giác ABC vuông tại A, đường cao AH. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?
(1) AB2=BH.CH
(2) AC2=CH.BC
(3) BC2=AB.AC
Đáp án : B
Xác định các tam giác đồng dạng suy ra tỉ số đồng dạng giữa các cạnh.
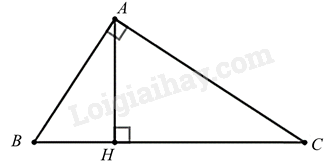
Ta có:
ΔABC∽ΔHBA(g.g)⇒ABBC=BHAB⇒AB2=BH.BC nên khẳng định (1) sai.
ΔABC∽ΔHAC(g.g)⇒ACBC=CHAC⇒AC2=CH.BC nên khẳng định (2) đúng.
Khẳng định (3) sai.
Vậy chỉ có 1 khẳng định đúng (khẳng định (2)).
Đáp án B.
Cho hình bình hành ABCD, kẻ AH⊥CD tại H; AK⊥BC tại K. Chọn câu trả lời đúng.
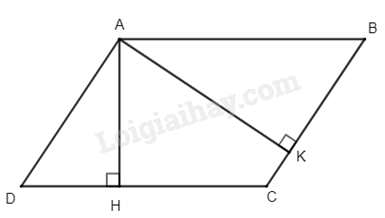
Đáp án : C
Dựa vào tính chất của hình bình hành và các trường hợp đồng dạng của hai tam giác vuông để xác định.
Hình bình hành ABCD có ˆB=ˆD
Xét ΔAHD và ΔAKB có:
ˆH=ˆK(=900)
ˆB=ˆD
suy ra ΔAHD∽ΔAKB(gg)
Các đỉnh tương ứng là: 2 đỉnh A, đỉnh D và đỉnh B, đỉnh H và đỉnh K nên đáp án C đúng.
Đáp án C.
Hình biểu diễn đúng tâm phối cảnh của cặp hình đồng dạng này là:
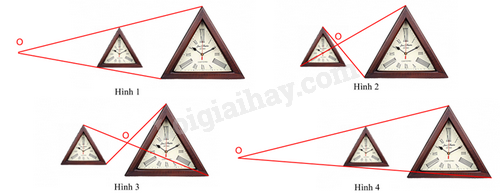
Đáp án : A
Xác định đúng các đỉnh của hai hình để nối được tâm phối cảnh của hai hình bên.
Trong các hình trên, chỉ có hình 1 biểu diễn đúng tâm phối cảnh của cặp hình đồng dạng này.

Đáp án A.
Hình chóp tam giác đều có bao nhiêu mặt?
Đáp án : B
Dựa vào đặc điểm của hình chóp tam giác đều.
Hình chóp tam giác đều có 4 mặt: 3 mặt bên và 1 mặt đáy.
Đáp án B.
Một chậu cây cảnh mini có hình dạng là một hình chóp tứ giác đều có chiều cao bằng 35cm, cạnh đáy bằng 24cm . Độ dài trung đoạn của chậu cây cảnh là

Đáp án : A
Gọi SI là trung đoạn, SO là đường cao của hình chóp đều S.ABCD.
Dựa vào tính chất của đường trung bình để tính OI.
Áp dụng định lí Pythagore vào tam giác SOI để tính SI.
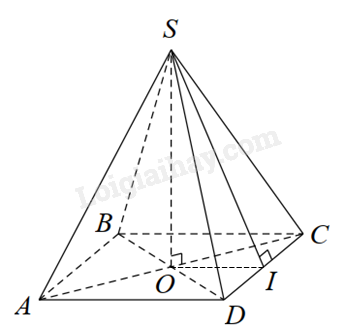
Gọi hình chóp đều S.ABCD là hình mô tả của chậu cây mini.
Gọi SO là đường cao của hình chóp, SO = 35cm.
Gọi SI là trung đoạn. Khi đó I là trung điểm của CD.
Xét ΔACD có O, I lần lượt là trung điểm của AC, CD nên OI là đường trung bình của ΔACD.
Suy ra OI=12AD=12.24=12(cm)
Xét ΔSOI vuông tại O có:
SI2=SO2+OI2=352+122=1369SI=√1369=37(cm)
Vậy độ dài trung đoạn của chậu cây cảnh là 37cm.
Đáp án A.
1. Giải các phương trình sau:
a) 2(x−3)=5(x−2)+8
b) x−19+x−37=2
2. Cho hàm số y=−2x+5 có đồ thị (d).
a) Trên mặt phẳng tọa độ Oxy, vẽ đồ thị (d). Gọi A, B lần lượt là giao điểm của (d) với các trục tọa độ Ox, Oy. Tính diện tích tam giác OAB.
b) Viết phương trình đường thẳng (d’) qua M(1;5) và song song với (d).
1. Đưa phương trình về dạng ax+b=0 để giải.
2.
a) Lấy 2 điểm A, B thuộc đồ thị hàm số. Vẽ đường thẳng đi qua 2 điểm đó ta được đồ thị (d).
Tính diện tích tam giác OAB vuông tại O: SΔOAB=12OA.OB.
b) Phương trình đường thẳng (d’) có dạng: y=ax+b(a≠0)
Hai đường thẳng y=ax+b(a≠0) và y=a′x+b′(a′≠0) song song nếu a=a′;b≠b′.
Tiếp theo thay tọa độ điểm M(1;5) vào phương trình đường thẳng (d’) để tìm được phương trình.
1. a) 2(x−3)=5(x−2)+8
2x−6=5x−10+82x−6=5x−22x−5x=−2+6−3x=4x=−43
Vậy x=−43
b) x−19+x−37=2
7(x−1)63+9(x−3)63=2.63637(x−1)+9(x−3)=2.637x−7+9x−27=1267x+9x=126+27+716x=160x=10
Vậy x=10
2. a) Cho x=0 thì y=5, ta được B(0;5) là giao điểm của (d) với các trục tọa độ Oy.
Cho y=0 thì x=52, ta được A(52;0) là giao điểm của (d) với các trục tọa độ Oy.
Đường thẳng AB chính là đồ thị (d).
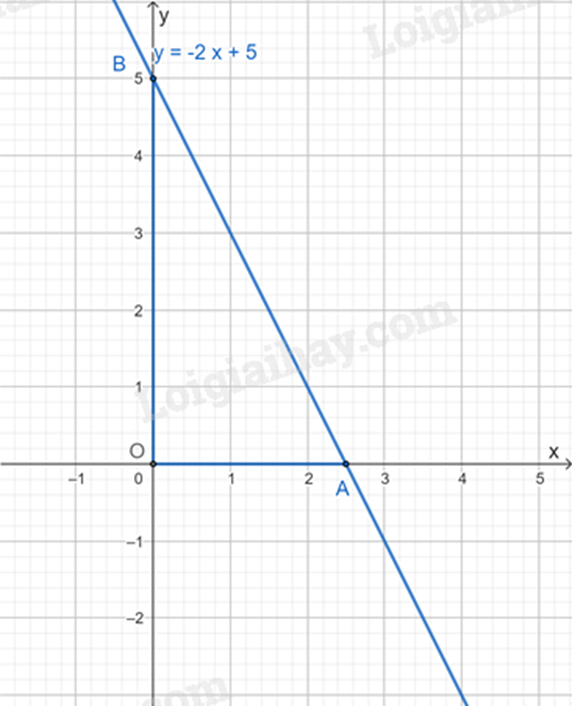
Vì A, B lần lượt là giao điểm của đường thẳng (d) và trục Ox, Oy nên OA⊥OB.
Suy ra ΔOAB vuông tại O.
Diện tích ΔOAB là: SΔOAB=12OA.OB=1252.5=254 (đơn vị diện tích).
b) Gọi phương trình (d’) cần tìm có dạng: y=ax+b(a≠0).
Vì đường thẳng (d’) song song với (d) nên a=−2,b≠5, khi đó phương trình đường thẳng trở thành:
y=−2x+b
Điểm M(1;5) thuộc đường thẳng (d’) nên ta có:
5=−2.1+bb=5+2b=7(TM)
Vậy phương trình đường thẳng cần tìm là y=−2x+7.
Giải bài toán bằng cách lập phương trình
Tổ sản xuất được giao dệt một số thảm trong 20 ngày. Nhưng do tổ tăng năng suất 20% nên đã hoàn thành sau 18 ngày. Không những vậy mà tổ còn làm thêm được 24 chiếc thảm. Tính số thảm thực tế tổ sản xuất làm được.
Giải bài toán bằng cách lập phương trình.
Gọi năng suất dự kiến của tổ sản suất là x (chiếc thảm) (x∈N∗).
Biểu diễn năng suất thực tế và số thảm làm được theo x và lập phương trình.
Giải phương trình và kiểm tra nghiệm.
Gọi năng suất của tổ sản suất là x (chiếc thảm) (x∈N∗).
Khi đó năng suất thực tế của tổ là: x+20%x=120%x=1,2x
Số thảm tổ cần dệt là: 20x (chiếc thảm)
Số thảm tổ làm được là: 18.1,2x=21,6x.
Vì tổ còn làm thêm được 24 chiếc thảm so với số thảm được giao nên ta có phương trình:
20x+24=21,6x
Giải phương trình ta được x=15(TM)
Vậy số thảm thực tế tổ sản xuất làm được là: 21,6.15=324 chiếc thảm.
Một cuốn lịch để bàn có hình dạng là một hình chóp tam giác đều có các mặt là các tam giác đều có cạnh bằng 20cm. Tính thể tích của cuốn lịch. (làm tròn đến chữ số thập phân thứ hai).

Sử dụng tính chất của đường cao trong tam giác đều để tính AI.
Dựa vào tính chất của trọng tâm để tính OI.
Vì các mặt đều là tam giác đều nên đường cao của các tam giác bằng nhau, tính được SI.
Áp dụng định lí Pythagore trong tam giác để tính SO.
Sử dụng công thức tính thể tích hình chóp đều để tính thể tích của S.ABC.
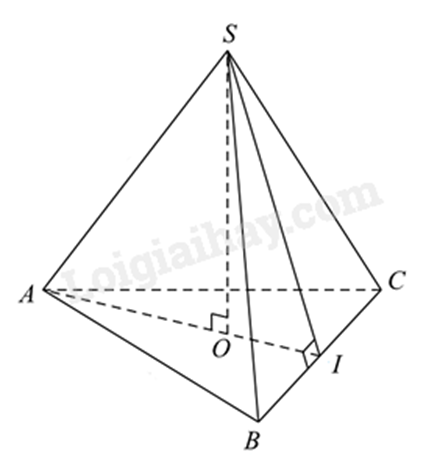
Xét ΔABC đều có đường cao AI=AC√32=20√32=10√3 (cm)
O là trọng tâm của tam giác ABC nên OI=13AI=13.10√3=10√33(cm).
Vì SI cũng là đường cao của tam giác đều SBC có cạnh bằng 20cm nên SI=AI=10√3cm.
Áp dụng định lí Pythagore vào tam giác vuông SOI, ta có:
SO2=SI2−OI2=(10√3)2−(10√33)2=8003SO=√8003=20√63
Thể tích hình chóp S.ABC là: V=13.20√63.12.10√3.20≈942,81(cm3)
Vậy thể tích của cuốn lịch khoảng 942,81cm3.
Cho ΔABC có ba góc nhọn (AB < AC). Kẻ đường cao AH, từ H kẻ HD và HE lần lượt vuông góc với AB và AC (D∈AB,E∈AC).
a) Chứng minh ΔAHD∽ΔABH.
b) Chứng minh AD.AB = AE.AC.
c) Gọi I là trung điểm của HC. Điểm F là chân đường vuông góc hạ từ I đến AC.
Chứng minh CA2−HC2=AF2−CF2
a) Chứng minh tam giác AHD và tam giác ABH đồng dạng theo trường hợp góc – góc.
b) Chứng minh ΔAHE∽ΔACH suy ra AH2=AE.AC
Dựa vào ý a suy ra AH2=AB.AD, ta được điều phải chứng minh.
c) Dựa vào định lí Pythagore suy ra CA2−HC2=AH2.
Chứng minh F là trung điểm của EC.
Sử dụng hằng đẳng thức hiệu hai bình phương để suy ra AF2−CF2=AH2.
Ta được điều phải chứng minh.
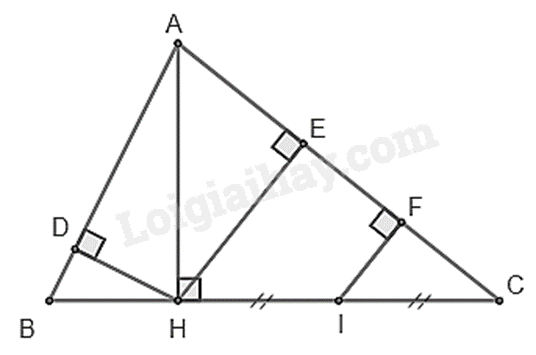
a) Xét ΔAHD và ΔABH có:
^ADH=^BHA=900
^BAH chung
nên ΔAHD∽ΔABH(g.g) (đpcm)
b) Xét ΔAHE và ΔACH có:
^AEH=^AHC=900
^HAC chung
nên ΔAHE∽ΔACH(g.g)
Suy ra AEAH=AHAC. Do đó AH2=AE.AC (1)
ΔAHD∽ΔABH(cmt) suy ra ADAH=AHAB. Do đó AH2=AB.AD (2)
Từ (1) và (2) suy ra AB.AD=AC.AE (đpcm)
c) Áp dụng định lí Pythagore vào tam giác vuông ACH, ta có:
CA2−HC2=AH2 (3)
Xét tam giác CHE có:
I là trung điểm của CH
FI//EH(FI⊥AC,HE⊥AC)
nên FI là đường trung bình của tam giác CHE.
Suy ra F là trung điểm của CE hay EF = FC.
Áp dụng hằng đẳng thức hiệu hai bình phương, ta có:
AF2−CF2=(AF−CF)(AF+CF)=(AF−EF).AC=AE.AC=AH2(4)
Từ (3) và (4) suy ra CA2−HC2=AF2−CF2. (đpcm)
Ở một trang trại nuôi chim cút, người ta nhận thấy xác suất một quả trứng cút có cân nặng dưới 9g là 0,5. Hãy ước lượng xem trong một lô 3000 quả trứng cút của trang trại có khoảng bao nhiêu quà trứng có cân nặng dưới 9g.
Số quả trứng có cân nặng dưới 9g = tổng số quả trứng . xác suất một quả trứng cút có cân nặng dưới 9g.
Trong lô 3000 quả trứng cút của trang trại, số quả trứng có cân nặng dưới 9g là:
3000.0,5=1500 (quả)
Vậy có khoảng 1500 quả trứng có cân nặng dưới 9g trong lô 3000 quả.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365