Trả lời câu hỏi Hoạt động 1 trang 19 SGK Toán 12 Kết nối tri thức

Xét hình phẳng giới hạn bởi đồ thị $y = f\left( x \right) = x + 1$, trục hoành và hai đường thẳng $x =  - 2,x = 1$ (H.4.12).

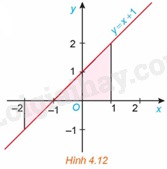
a) Tính diện tích S của hình phẳng này.

b) Tính $\int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx}$ và so sánh với S.

Trả lời câu hỏi Luyện tập 1 trang 20 SGK Toán 12 Kết nối tri thức

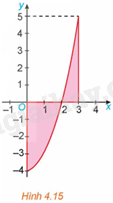
Tính diện tích hình phẳng giới hạn bởi parabol $y = {x^2} - 4$, trục hoành và hai đường thẳng $x = 0,x = 3$ (H.4.15).

Trả lời câu hỏi Hoạt động 2 trang 20 SGK Toán 12 Kết nối tri thức

Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $f\left( x \right) =  - {x^2} + 4x,$ $g\left( x \right) = x$ và hai đường thẳng $x = 1,x = 3$ (H.4.16)

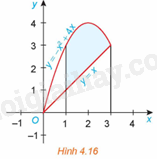
a) Giả sử ${S_1}$ là diện tích hình phẳng giới hạn bởi parabol $y =  - {x^2} + 4x$, trục hoành và hai đường thẳng $x = 1,x = 3$; ${S_2}$ là diện tích hình phẳng giới hạn bởi đường thẳng $y = x$, trục hoành và hai đường thẳng $x = 1,x = 3$. Tính ${S_1}$, ${S_2}$ và từ đó suy ra S.

b) Tính $\int\limits_1^3 {\left| {f\left( x \right) - g\left( x \right)} \right|dx}$ và so sánh với S.

Trả lời câu hỏi Luyện tập 2 trang 21 SGK Toán 12 Kết nối tri thức

Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y = \sqrt x ,y = x - 2$ và hai đường thẳng $x = 1,x = 4$.

Trả lời câu hỏi Vận dụng 1 trang 22 SGK Toán 12 Kết nối tri thức

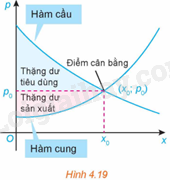
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau $\left( {{x_o};{p_o}} \right)$ của đồ thị hàm cầu $p = D\left( x \right)$ và đồ thị hàm cung $p = S\left( x \right)$ được gọi là điểm cân bằng.

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang $p = {p_o}$ và đường thẳng đứng $x = 0$ là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang $p = {p_o}$ và đường thẳng đứng $x = 0$ được gọi là thặng dư sản xuất, như trong Hình 4.19.

(Theo R. Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009)

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: $p =  - 0,36x + 9$ và hàm cung: $p = 0,14x + 2$, trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.