Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 1 Toán 12 - Kết nối tri thức
Đề thi giữa kì 1 Toán 12 - Đề số 3
Đề thi giữa kì 1 Toán 12 - Đề số 4 Đề thi giữa kì 1 Toán 12 - Đề số 5 Đề thi giữa kì 1 Toán 12 - Đề số 6 Đề thi giữa kì 1 Toán 12 - Đề số 7 Đề thi giữa kì 1 Toán 12 - Đề số 8 Đề thi giữa kì 1 Toán 12 - Đề số 2 Đề thi giữa kì 1 Toán 12 - Đề số 1Đề thi giữa kì 1 Toán 12 - Đề số 3
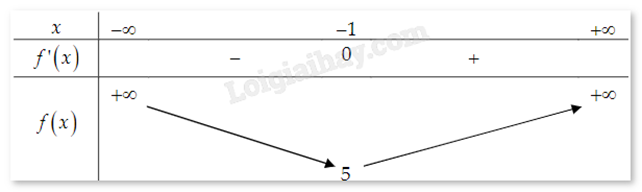
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số y = f(x) xác định trên R{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình. Mệnh đề nào dưới đây đúng?
Cho hàm số y = f(x) xác định trên R\{-1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình. Mệnh đề nào dưới đây đúng?
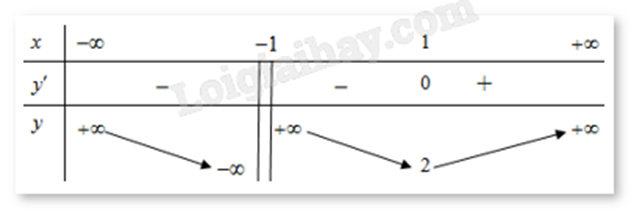
Hàm số nghịch biến trên (−∞;−1)
Hàm số nghịch biến trên (−∞;+∞)
Hàm số đồng biến trên khoảng (−1;+∞)
Hàm số đồng biến trên khoảng (−∞;1)
Đáp án : A
Quan sát bảng biến thiên và nhận xét.
Dựa vào bảng biến thiên ta thấy trên khoảng (−∞;−1) đạo hàm y' < 0 nên hàm số nghịch biến.
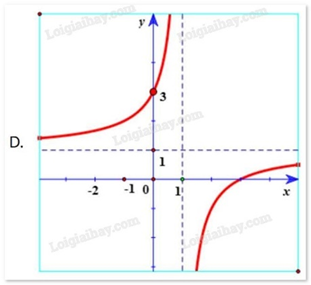
Hàm số y=x−2x−1 có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
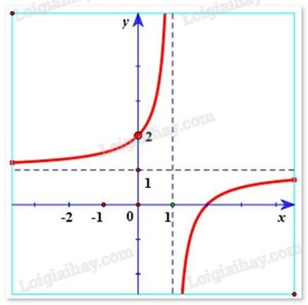
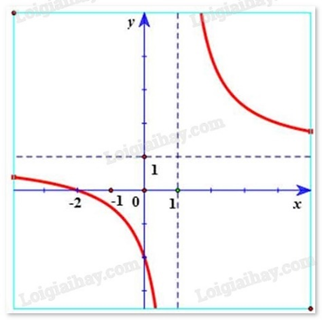
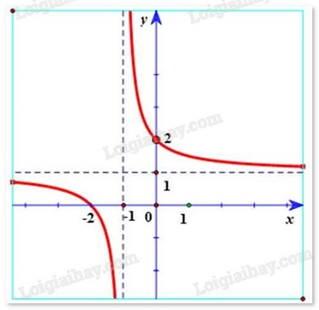
Đáp án : A
Quan sát đồ thị và nhận xét.
Hàm số y=x−2x−1 có tiệm cận đứng x = 1. Tiệm cận ngang y = 1 nên loại trường hợp D.
Đồ thị hàm số y=x−2x−1 đi qua điểm (0; 2) nên chọn đáp án A.
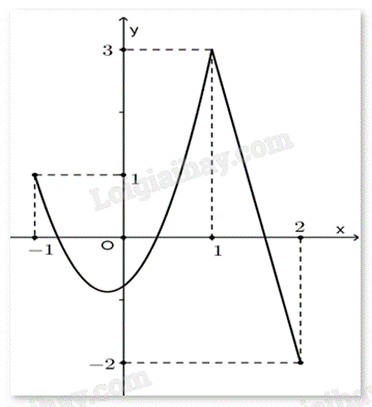
Cho hàm số y = f(x) liên tục trên đoạn [–1;2] và có đồ thị như hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–1;2]. Tính M + 2m.
y = 2
y = -1
y = 0
y = 1
Đáp án : B
Quan sát đồ thị và nhận xét.
M=max[−1;2]f(x)=f(1)=3.
M=min[−1;2]f(x)=f(2)=−2.
Vậy M + 2m = 3 + 2.(-2) = -1.
Cho hàm số y = f(x) có bảng biến thiên như sau:

Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là:
4
1
3
2
Đáp án : C
Quan sát bảng biến thiên và nhận xét các giới hạn.
Ta có:
limx→−∞f(x)=2 nên ta có tiệm cận ngang y = 2.
limx→+∞f(x)=5 nên ta có tiệm cận ngang y = 5.
limx→1−f(x)=+∞ nên ta có tiệm cận đứng x = 1.
Vậy tổng số tiệm cận đứng và tiệm cận ngang là 3.
Đường tiệm cận xiên của đồ thị hàm số y=x2+4x−7x−2 là:
y = x + 6
y = x – 6
y = 6x
y = 6
Đáp án : A
Thực hiện phép chia đa thức (ở tử) cho đa thức (ở mẫu) ta được y=ax+b+Mcx+d(a≠0) với M là hằng số.
Đường thẳng y = ax + b (a≠0) gọi là đường tiệm cận xiên của đồ thị hàm số y = f(x) nếu limx→+∞[f(x)−(ax+b)]=0 limx→−∞[f(x)−(ax+b)]=0.
Kết luận đường thẳng y = ax + b là đường tiệm cận xiên của đồ thị hàm số.
Ta có: y=x2+4x−7x−2=x+6+5x−2=f(x).
Từ đó: limx→+∞[f(x)−(x+6)]=limx→+∞5x−2=0.
Vậy đường thẳng y = x + 6 là đường tiệm cận xiên của đồ thị hàm số đã cho.
Tọa độ tâm đối xứng của đồ thị hàm số y=x+4x−3 là:
(3;1)
(1;3)
(3;-4)
(3;4)
Đáp án : A
Tìm tiệm cận ngang và tiệm cận đứng của đồ thị và tìm giao điểm của chúng.
Tiệm cận ngang của đồ thị là y = 1, tiệm cận đứng của đồ thị là x = 3 nên tâm đối xứng có tọa độ (3;1).
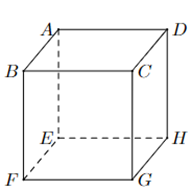
Cho hình hộp ABCD.EFGH. Kết quả phép toán →AB−→EH là
→BD
→AE
→BH
→DB
Đáp án : D
Dựa vào định nghĩa các vecto bằng nhau, quy tắc cộng, trừ vecto.
Ta có: →AB=→EF, →DB=→HF vì chúng cùng độ dài và cùng hướng.
→AB−→EH=→EF+→HE=→HF=→DB.
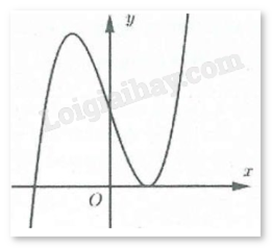
Đường cong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
y=x3−3x2+2
y=x2−x+1
y=x+3x−2
y=−x3+3x2+2
Đáp án : A
Quan sát đồ thị và nhận xét.
Dựa vào đồ thị ta thấy có hai điểm cực trị nên đây là hàm số bậc ba.
Mặt khác, limx→+∞y=+∞ nên hệ số a > 0.
Giá trị lớn nhất của hàm số y=√25−x2 trên đoạn [-4;4] là:
5
4
3
0
Đáp án : A
Tìm đạo hàm của hàm số sau đó tính các giá trị f(x).
f′(x)=−x√25−x2=0⇔x=0.
Ta có: f(-4) = 4; f(0) = 5; f(4) = 3.
Vậy giá trị lớn nhất của hàm số y=√25−x2 trên đoạn [-4;4] bằng 5.
Cho hàm số y = f(x) có đạo hàm f′(x)=x(x−2)(x2−4)(x+1). Hàm số y = f(x) có bao nhiêu điểm cực trị?
3
2
4
5
Đáp án : A
Cực trị của hàm số f(x) là nghiệm bội lẻ của phương trình f’(x) = 0.
Ta có: f’(x) = 0 có 3 nghiệm bội lẻ là x = 0, x = 2 và x = -1, tương ứng với 3 điểm cực trị.
Trong không gian với hệ tọa độ Oxyz, cho vecto →u=2→j+3→i−→k. Tọa độ của vecto →u là
(2;1;-3)
(2;3;-1)
(3;2;-1)
(2;1;3)
Đáp án : C
Trong không gian có hệ trục tọa độ Oxyz, →i,→j,→k lần lượt là các vecto đơn vị trên các trục Ox, Oy, Oz.
Tọa độ của vecto →u là (3;2;-1).
Cho hai vecto →u=(2;−1;3), →v=(−3;4;1). Tích →u.→v bằng:
11
-7
5
-2
Đáp án : B
Sử dụng công thức tính tọa độ tích vô hướng của hai vecto.
Ta có: →u.→v=2.(−3)+(−1).4+3.1=−7.
Cho hàm số f(x) xác định trên R có bảng biến thiên như sau:
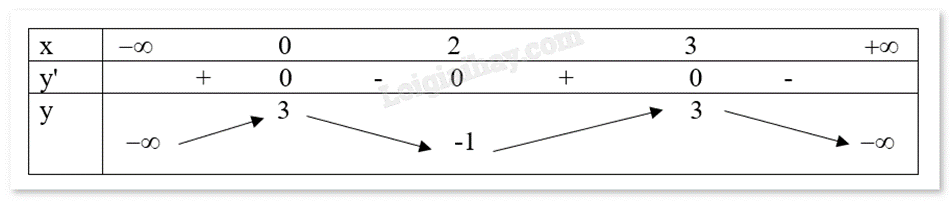
a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị lớn nhất bằng 3
Hàm số đạt cực tiểu tại x = -1
d) Hàm số đạt cực tiểu tại x = -1
a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị lớn nhất bằng 3
Hàm số đạt cực tiểu tại x = -1
d) Hàm số đạt cực tiểu tại x = -1
Quan sát bảng biến thiên và nhận xét.
a) Sai. Hàm số f(x) nghịch biến trên (0;2).
b) Đúng. Số điểm cực trị của hàm số đã cho là 3 (x = 0, x = 2, x = 3).
c) Đúng. Hàm số f(x) có giá trị lớn nhất là 3.
d) Sai. Hàm số đạt cực tiểu tại x = 2.
Cho hàm số f(x)=−x4+12x2+1.
a) Hàm số f(x) đồng biến trên khoảng (1;37)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [-1;2] bằng 12
d) Hàm số f(x) có giá trị lớn nhất trên đoạn [-1;2] bằng 33
a) Hàm số f(x) đồng biến trên khoảng (1;37)
b) Số điểm cực trị của hàm số đã cho là 3
c) Hàm số f(x) có giá trị nhỏ nhất trên đoạn [-1;2] bằng 12
d) Hàm số f(x) có giá trị lớn nhất trên đoạn [-1;2] bằng 33
Lập bảng biến thiên và nhận xét.
f′(x)=−4x3+24x2=0 khi x=√6, x=−√6 hoặc x = 0.
Bảng biến thiên:
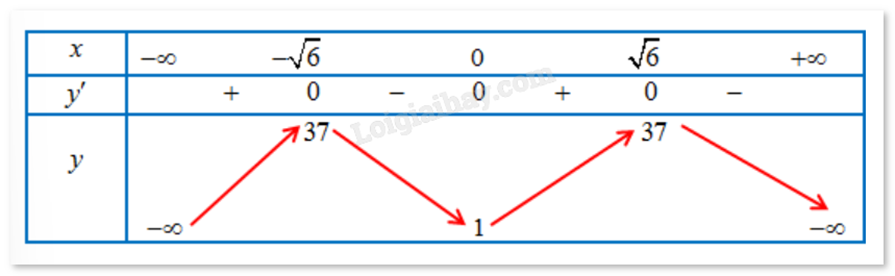
Ta có: f(-1) = 12; f(2) = 33; f(0) = 1.
a) Sai. Hàm số f(x) nghịch biến trên .
b) Đúng. Hàm số có ba điểm cực trị (, x = 0, ).
c) Sai. Hàm số f(x) có giá trị nhỏ nhất trên [-1;2] bằng 1.
d) Đúng. Hàm số f(x) có giá trị lớn nhất trên [-1;2] bằng 33.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và G là trọng tâm tam giác SBD.
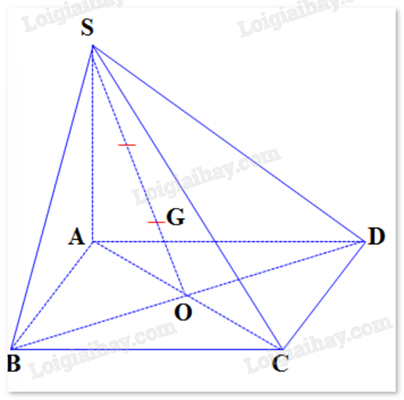
a) →SG=23→SO
b) →AS+→AB+→AD=→AG
c) →SA+→SC=3→SG
d) →SA+→SB+→SC+→SD=12→GO
a) →SG=23→SO
b) →AS+→AB+→AD=→AG
c) →SA+→SC=3→SG
d) →SA+→SB+→SC+→SD=12→GO
Sử dụng quy tắc cộng vecto, lý thuyết các vecto bằng nhau, vecto đối nhau, quy tắc trọng tâm.
a) Đúng. Vì hai vecto →SG, →SO cùng hướng và |→SG|=23|→SO|.
b) Sai. Vì →AS+→AB+→AD=3→AG (quy tắc trọng tâm)
c) Đúng. Vì →SA+→SC=2→SO=2.23→SG=3→SG.
d) Đúng. Vì →SA+→SB+→SC+→SD=→SA+→SC+→SB+→SD=2→SO+2→SO
=4→SO=4.3→GO=12→GO.
Trong không gian Oxyz, cho vecto →a=(1;2;3), →b=(3;6;9).
a) →b−→a=(2;4;6)
b) →a và →b cùng phương
c) |→a|=√6
d) −→b=3→i+6→j+9→k
a) →b−→a=(2;4;6)
b) →a và →b cùng phương
c) |→a|=√6
d) −→b=3→i+6→j+9→k
Sử dụng các quy tắc cộng, trừ vecto, nhân vecto với một số, khái niệm hai vecto cùng phương, công thức tính độ dài vecto.
a) Đúng. Vì →b−→a=(3−1;6−2;9−3)=(2;4;6).
b) Đúng. Vì 13=26=39 nên →a và →b cùng phương.
c) Sai. Vì |→a|=√12+22+32=√14.
d) Sai. Vì −→b=(−3;−6;−9)=−3→i−6→j−9→k.
Giá trị nhỏ nhất của hàm số f(x)=x2+3x−1 trên đoạn [2;4] bằng bao nhiêu?
Đáp án:
Đáp án:
- Tính y’, tìm các nghiệm của y’ = 0
- Tìm giá trị y tại các điểm cực trị của hàm số và hai đầu mút của đoạn.
Ta có: f′(x)=x2−2x−3(x−1)2=0 khi x = -1 hoặc x = 3.
Xét đoạn [2;4] có: f(2) = 7; f(3) = 6; f(4)=193.
Vậy giá trị nhỏ nhất của hàm số trên [2;4] là 6.
Tìm điều kiện của tham số m để đồ thị của hàm số y=(2m+1)x+3x+1 có đường tiệm cận đi qua điểm A(-2;7).
Đáp án:
Đáp án:
Sử dụng quy tắc tìm đường tiệm cận của hàm phân thức.
Nếu m = 1, ta có hàm số y=3x+3x+1=3 không có tiệm cận qua A(-2;7).
Nếu m≠1, đồ thị có tiệm cận đứng x = -1 và tiệm cận ngang y = 2m + 1.
Như vậy, để thỏa mãn yêu cầu đề bài, tiệm cận ngang phải đi qua A, khi và chỉ khi 2m + 1 = 7, tức m = 3.
Một cửa hàng bán một loại sản phẩm với lợi nhuận thu được khi bán x (trăm) sản phẩm được mô tả bởi hàm số L(x)=−0,5x2+6x−10. Trong đó, x là số lượng sản phẩm bán ra, L(x) là lợi nhuận thu được (đơn vị: triệu đồng). Hãy xác định số lượng sản phẩm mà cửa hàng cần bán ra để lợi nhuận đạt mức cao nhất.
Đáp án:
Đáp án:
Tìm x để hàm số L(x)=−0,5x2+6x−10 đạt giá trị lớn nhất.
Lợi nhuận đạt mức cao nhất khi L(x)=−0,5x2+6x−10 đạt giá trị lớn nhất.
Ta có: L′(x)=−x+6=0⇔x=6.
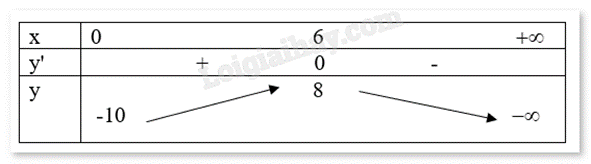
Theo bảng biến thiên, L(x) đạt giá trị lớn nhất khi x = 6 (trăm).
Vậy lợi nhuận đạt mức cao nhất khi bán ra 600 sản phẩm.
Cho parabol (P): y=x2 và điểm A(-3;0). Xác định điểm M thuộc (P) sao cho khoảng cách AM là ngắn nhất. Tung độ của điểm M bằng bao nhiêu?
Đáp án:
Đáp án:
Thiết lập hàm số biểu diễn bình phương độ dài AM theo biến x là hoành độ. Lập bảng biến thiên cho hàm số, tìm x để hàm số đó đạt giá trị nhỏ nhất.
Gọi M(x;x2) là một điểm bất kì của parabol (P).
Ta có: AM2=(x+3)2+x4=x4+x2+6x+9.
AM nhỏ nhất khi và chỉ khi f(x)=AM2 nhỏ nhất.
Xét f(x)=x4+x2+6x+9.
Có f′(x)=4x3+2x+6=0⇔x=−1.
Dựa vào bảng biến thiên, ta suy ra f(x) đạt giá trị nhỏ nhất tại x = -1.
Như vậy, điểm M cần tìm có tọa độ (-1;1). Tung độ của M bằng 1.
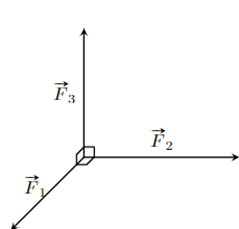
Ba lực →F1,→F2,→F3 cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2N; 3N; 4N. Hợp lực của ba lực đã cho có độ lớn bao nhiêu Niu-tơn (kết quả làm tròn đến một chữ số thập phân)?
Đáp án:
Đáp án:
Sử dụng quy tắc hình hộp.
Vì ba vecto trên đôi một vuông góc nên ta có thể áp dụng quy tắc hình hộp. Hợp lực F của ba vecto trên có độ lớn là:
F=√F21+F22+F23=√22+32+42=√29≈5,4 (N).
Trong không gian Oxy (đơn vị đo lấy theo km), radar phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800;500;7) đến điểm B(940;550;8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên tốc độ và hướng bay thì tọa độ của máy bay sau 10 phút tiếp theo là D(x;y;x). Khi đó, x + y + z bằng bao nhiêu?
Đáp án:
Đáp án:
Sử dụng quy tắc cộng vecto.
Máy bay di chuyển với tốc độ không đổi, sau 10 phút sẽ đi được quãng đường đúng bằng quãng đường 10 phút trước, tức AB = BD.
Mặt khác, hướng bay giữ nguyên nên →AB=→BD=(940−800;550−500;8−7)=(140;50;1).
Ta tính được D=(940+140;550+50;8+1)=(1080;600;9).
Vậy x + y + z = 1689.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365