1. Công thức xác suất toàn phần

Ví dụ 1: Theo một số liệu thống kê, năm 2004 ở Canada có 65% nam giới là thừa cân và 53,4% nữ giới là thừa cân. Nam giới và nữ giới ở Canada đều chiếm 50% dân số cả nước (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Hỏi rằng, trong năm 2004, xác suất để một người Canada được chọn ngẫu nhiên là người thừa cân bằng bao nhiêu?

Giải:

Xét hai biến cố sau:

A: “Người được chọn ra là người thừa cân”;

B: “Người được chọn ra là nam giới” (biến cố $\overline B$: “Người được chọn ra là nữ giới”).

Từ giả thiết ta có:

$P(B) = P(\overline B ) = 50\%  = 0,5$; $P(A|B) = 65\%  = 0,65$, $P(A|\overline B ) = 53,4\%  = 0,534$.

Theo công thức xác suất toàn phần, ta có:

$P(A) = P(B).P(A|B) + P(\overline B ).P(A|\overline B ) = 0,5.0,65 + 0,5.0,534 = 0,592$.

Vậy xác suất để một người Canada được chọn ngẫu nhiên là người thừa cân bằng 0,592.

Lối cách khác, tỉ lệ người Canada thừa cân là 59,2%.

Ví dụ 2: Trong trò chơi hái hoa có thưởng của lớp 12A, cô giáo treo 10 bông hoa trên cành cây, trong đó có 5 bông hoa chưa phiếu có thưởng. Bạn Bình hái bông hoa đầu tiên sau đó bạn An hái bông hoa thứ hai.

a) Vẽ sơ đồ hình cây biểu thị tình huống trên.

b) Từ đó, tính xác suất bạn An hái được bông hoa chứa phiếu có thưởng.

Giải:

Xét hai biến cố:

A: “Bông hoa bạn An hái được chứa phiếu có thưởng”.

B: “Bông hoa bạn Bình hái được chứa phiếu có thưởng”.

Khi đó, ta có:

$P(B) = \frac{5}{{10}} = \frac{1}{2}$, $P(\overline B ) = 1 - P(B) = 1 - \frac{1}{2} = \frac{1}{2}$, $P(A|B) = \frac{4}{9}$, $P(A|\overline B ) = \frac{5}{9}$.

a) Sơ đồ hình cây biểu thị tình huống đã cho là:

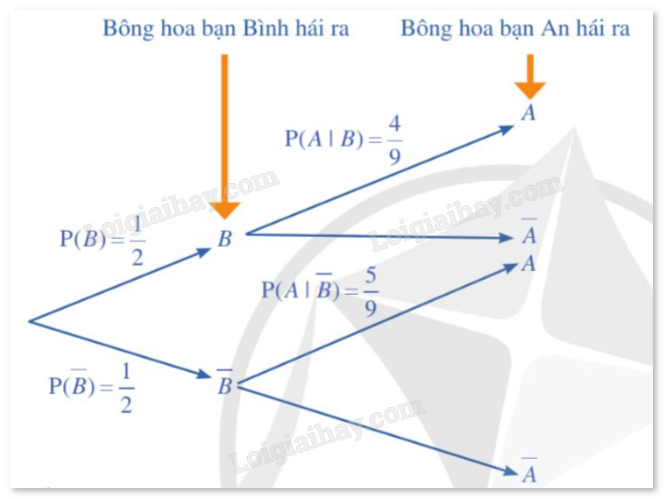
b) Áp dụng công thức xác suất toàn phần, ta có:

$P(A) = P(B).P(A|B) + P(\overline B ).P(A|\overline B ) = \frac{1}{2}.\frac{4}{9} + \frac{1}{2}.\frac{5}{9} = \frac{1}{2}$.

Vậy xác suất bạn An hái được bông hoa chứa phiếu có thưởng bằng $\frac{1}{2}$.

2. Công thức Bayes

Nhận xét: Cho hai biến cố A, B với P(A) > 0, 0 < P(B) < 1. Do $P(A) = P(A \cap B) + (A \cap \overline B ) = P(B).P(A|B) + P(\overline B ).P(A|\overline B )$nên công thức Bayes còn có dạng $P(B|A) = \frac{{P(B).P(A|B)}}{{P(B).P(A|B) + P(\overline B ).P(A|\overline B )}}$.

Ví dụ 1: Cho hai biến cố A, B sao cho P(A) = 0,6; P(B) = 0,4; P(A|B) = 0,3. Tính P(B|A).

Giải:

Áp dụng công thức Bayes, ta có: $P(B|A) = \frac{{P(B).P(A|B)}}{{P(A)}} = \frac{{0,4.0,3}}{{0,6}} = 0,2$.

Ví dụ 2: Giả sử có một loại bệnh mà tỷ lệ người mắc bệnh là 0,1%. Giả sử có một loại xét nghiệm, mà ai mắc bệnh khi xét nghiệm cũng có phản ứng dương tính, nhưng tỷ lệ phản ứng dương tính giả là 5% (tức là trong số những người không bị bệnh có 5% số người xét nghiệm lại có phản ứng dương tính).

a) Vẽ sơ đồ hình cây biểu thị tình huống trên.

b) Khi một người xét nghiệm có phản ứng dương tính thì khả năng mắc bệnh của người đó bao nhiêu phần trăm (làm tron kết quả đánh hàng phần trăm)?

Giải:

a) Xét hai biến cố:

K: “Người được chọn ra không mắc bệnh”.

D: “Người được chọn ra có phản ứng dương tính”.

Do tỷ lệ mắc bệnh là 0,1% = 0,001 nên P(K) = 1 - 0,001 = 0,999.

Trong số những người mắc bệnh có 5% số người có phản ứng dương tính nên P(D|K) = 5% = 0,05. Vì ai mắc bệnh khi xét nghiệm cũng phản ứng dương tính nên $P(D|\overline K ) = 1$.

Sơ đồ hình cây ở Hình 3 biểu thị tình huống đã cho.

b) Ta thấy: Khả năng mắc bệnh của một người xét nghiệm có phản ứng dương tính chính là $P(\overline K |D)$. Áp dụng công thức Bayes, ta có:

$P(\overline K |D) = \frac{{P(\overline K ).P(D|\overline K )}}{{P(\overline K ).P(D|\overline K ) + P(K).P(D|K)}} = \frac{{0,001}}{{0,001 + 0,999.0,05}} = 1,96\%$.

Vậy xác suất mắc bệnh của một người xét nghiệm có phản ứng dương tính là 1,96%.