Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 8 - Cánh diều
Đề thi giữa kì 2 Toán 8 Cánh diều - Đề số 9
Đề thi giữa kì 2 Toán 8 Cánh diều - Đề số 10 Đề thi giữa kì 2 Toán 8 - Đề số 8 - Cánh diều Đề thi giữa kì 2 Toán 8 - Đề số 7 - Cánh diều Đề thi giữa kì 2 Toán 8 - Đề số 6 - Cánh diều Đề thi giữa kì 2 Toán 8 - Đề số 5 - Cánh diều Đề thi giữa kì 2 Toán 8 - Đề số 4 - Cánh diều Đề thi giữa kì 2 Toán 8 - Đề số 3 - Cánh diều Đề thi giữa kì 2 Toán 8 - Đề số 2 - Cánh diều Đề thi giữa kì 2 Toán 8 - Đề số 1 - Cánh diềuĐề thi giữa kì 2 Toán 8 Cánh diều - Đề số 9
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho các dữ liệu sau đây, dữ liệu nào không phải dữ liệu định lượng?
Thời gian tự học ở nhà (đơn vị: giờ) của các bạn trong lớp.
Lượng mưa trung bình (đơn vị: mm) của các tháng trong năm 2022 tại Thành Phố Hồ Chí Minh.
Xếp loại học tập của học sinh lớp 8A.
Số học sinh nữ của mỗi lớp trong khối 8.
Đáp án : C
Dữ liệu định lượng là những dữ liệu thống kê là số (số liệu) được biểu diễn bằng số thực.
Thời gian (đơn vị: giờ) là số liệu.
Lượng mưa (đơn vị: mm) là số liệu.
Xết loại học tập: giỏi, khá, trung bình,… nên không phải số liệu.
Số học sinh là số liệu.
Đáp án C
Quan sát bảng số liệu sau đây cho biết dữ liệu của lớp nào đang không hợp lí?

8A.
8B.
8C.
8D.
Đáp án : C
Từ bảng số số liệu, xác định xem dữ liệu nào không hợp lí.
Vì lớp 8C chỉ có 45 học sinh nên số học sinh tham gia thi giữa kì II môn Toán là 47 học sinh là dữ liệu không hợp lí.
Đáp án C
Cho biểu đồ biểu diễn tổng doanh thu du lịch (ước đạt) (đơn vị: tỉ đồng) của tỉnh Khánh Hoà trong các năm 2018, 2019, 2020.
Tổng doanh thu du lịch trong năm 2020 giảm bao nhiêu so với năm 2019?
20 153,6 tỉ đồng.
20 153,8 tỉ đồng.
20 154 tỉ đồng.
20 153 tỉ đồng.
Đáp án : B
Xác định doanh thu của năm 2019, 2020.
Để tính số lượng giảm ta lấy tổng doanh thu năm 2019 – doanh thu năm 2020.
Tổng doanh thu du lịch trong năm 2019 là: 27 100 tỉ đồng.
Tổng doanh thu du lịch trong năm 2020 là: 6 946,2 tỉ đồng.
Tổng doanh thu du lịch trong năm 2020 giảm so với năm 2019 là:
27 100 - 6 946,2 = 20 153,8 (tỉ đồng)
Đáp án B
Một hộp đựng 10 chiếc bút bi gồm 3 màu xanh, 4 màu đen và 3 màu đỏ. Không nhìn và lấy ngẫu nhiên một chiếc bút. Có bao nhiêu kết quả có thể xảy ra
10.
4.
3.
6.
Đáp án : A
Kết quả có thể là tất cả các kết quả có thể xảy ra của hành động, thực nghiệm trong các trường hợp có thể xác định được.
Vì hộp có 10 chiếc bút nên có 10 kết quả có thể xảy ra khi lấy ngẫu nhiên một chiếc bút.
Đáp án A
Trong trò chơi tung đồng xu. Xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt sấp” là
12.
13.
14.
15.
Đáp án : A
Dựa vào kiến thức về xác suất của biến cố trong trò chơi tung đồng xu.
Trong trò chơi tung đồng xu, xác suất của biến cố “Mặt xuất hiện của đồng xu là mặt sấp” bằng 12.
Đáp án A
Hùng tập ném bóng vào rổ. Khi thực hiện ném 100 lần thì có 65 lần bóng ra ngoài rổ. Tính xác suất thực nghiệm của sự kiện ném bóng vào rổ.
720.
713.
1320.
12.
Đáp án : A
- Tính số lần ném bóng vào rổ.
- Tính xác suất thực nghiệm:

Số lần ném bóng vào rổ là: 100 – 65 = 35 (lần)
Xác suất thực nghiệm của sự kiện ném bóng vào rổ là: 35100=720.
Đáp án A
Cho hình vẽ: Đoạn thẳng nào là đường trung bình của tam giác ABC?
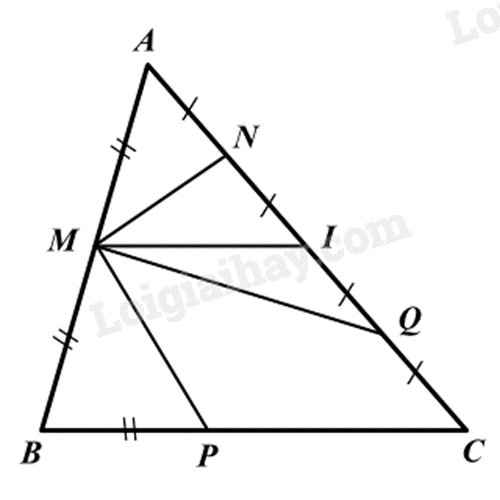
MP.
MN.
MI.
MQ.
Đáp án : C
Dựa vào khái niệm đường trung bình của tam giác: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Vì AN = NI = IQ = IC nên AN + NI = IQ + QC hay AI = IC
Xét tam giác ABC có:
AM = MB, AI = IC (M ∈ AB, I ∈ AC)
nên MI là đường trung bình của tam giác ABC.
Đáp án C
Cho tam giác ΔABC vuông tại A, biếtAB=6cm. Gọi M,N lần lượt là trung điểm của AB,AC và MN=5cm. Khi đó, độ dài AC là:
10cm.
3cm.
8cm.
11cm.
Đáp án : C
Chứng minh MN là đường trung bình của tam giác để suy ra BC.
Áp dụng định lí Pythagore vào tam giác vuông ABC để tính AC.
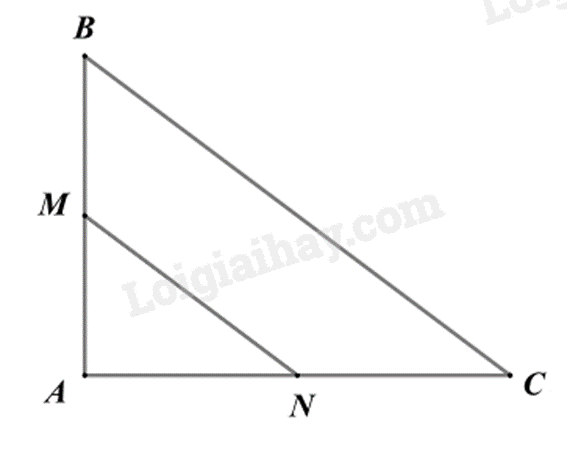
Xét tam giác ABC có:
M,N lần lượt là trung điểm của AB,AC nên MN là đường trung bình của tam giác ABC.
Do đó MN=12BC, suy ra BC=2MN=2.5=10(cm)
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
BC2=AB2+AC2
suy ra AC2=BC2−AB2=102−62=64, suy ra AC=√64=8(cm)
Đáp án C
Một cột đèn cao 10m chiếu sáng một cây xanh (như hình vẽ). Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét).
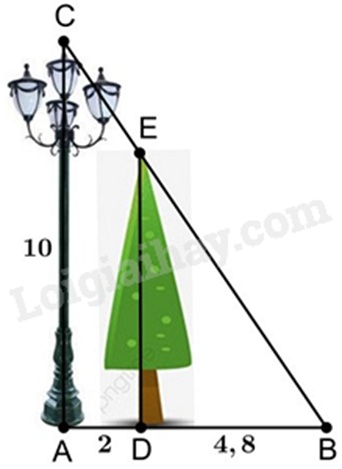
Khi đó, chiều cao của cây xanh là (làm tròn đến mét):
DE≈14m.
DE≈5m.
DE≈24m.
DE≈7m.
Đáp án : D
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Vì cột đèn và cây xanh cùng vuông góc với mặt đất nên chúng song song với nhau, hay DE // AC.
Suy ra BDAB=DEAC, hay BDAD+DB=DEAC
Thay số: 4,82+4,8=DE10, suy ra DE=4,8.106,8≈7(m)
Đáp án D
Cho ΔABC có AB=4cm;AC=9cm. Gọi AD là tia phân giác của ^BAC . Tính tỉ số CDBD.
94.
49.
45.
54.
Đáp án : A
Sử dụng Tính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
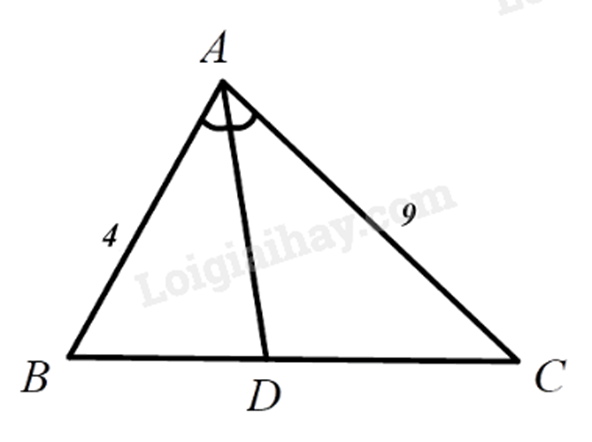
Vì AD là đường phân giác của tam giác ABC nên CDBD=ACAB=94.
Đáp án A
Cho ΔABC, tia phân giác góc trong của góc A cắt BC tại D. Cho AB=6, AC=x,BD=9,BC=21. Tính kết quả đúng của độ dài cạnh x?
x=14.
x=6.
x=12.
x=8.
Đáp án : D
Sử dụng Tính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
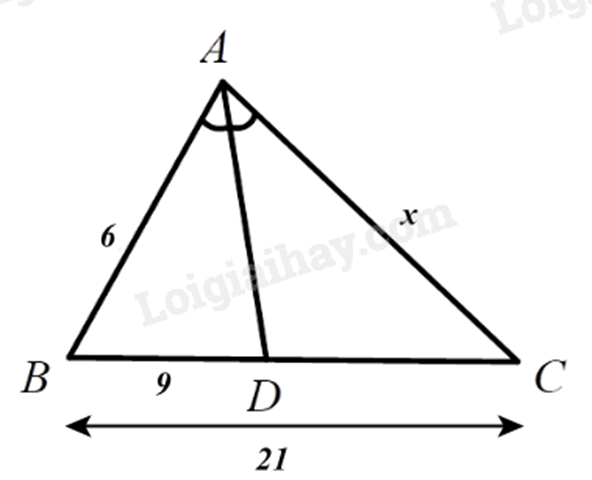
Vì D∈BC nên BD+DC=BC, suy ra CD=BC−BD=21−9=12.
Vì AD là đường phân giác của tam giác ABC nên ABAC=BDCD.
Thay số: 6x=912, suy ra x=6.129=8.
Đáp án D
Tìm x trong hình sau:
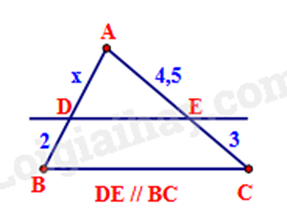
x = 4,5.
x = 3.
x = 1,33.
x = 6,75.
Đáp án : B
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Vì DE // BC nên ADDB=AEEC
Thay số: x2=4,53, suy ra x=4,5.23=3.
Đáp án B
Cho biểu đồ sau biểu diễn hiện trạng sử dụng đất ở Hà Nội và Hải Dương tính đến ngày 31 tháng 12 năm 2020 đối với đất sản xuất nông nghiệp, đất lâm nghiệp, đất ở.
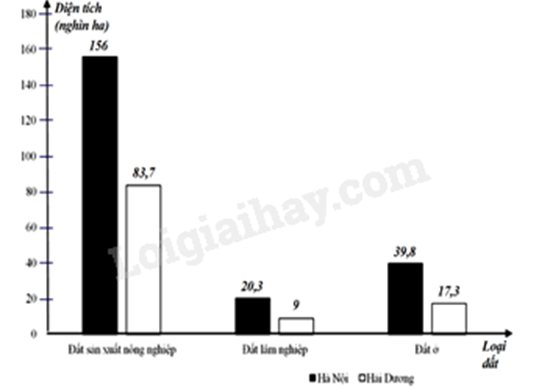
a) Loại đất là dữ liệu định lượng.
b) Bảng thống kê diện tích các loại đất được biểu diễn như sau:

c) Tổng diện tích các loại đất của Hà Nội là 216,1 nghìn ha.
d) Một bài báo có nêu thông tin: Theo thống kê năm 2020, diện tích đất ở của Hải Dương chỉ bằng khoảng 20,67% diện tích đất sản xuất nông nghiệp.
a) Loại đất là dữ liệu định lượng.
b) Bảng thống kê diện tích các loại đất được biểu diễn như sau:

c) Tổng diện tích các loại đất của Hà Nội là 216,1 nghìn ha.
d) Một bài báo có nêu thông tin: Theo thống kê năm 2020, diện tích đất ở của Hải Dương chỉ bằng khoảng 20,67% diện tích đất sản xuất nông nghiệp.
a) Dữ liệu định lượng là những dữ liệu thống kê là số (số liệu) được biểu diễn bằng số thực.
b) Từ biểu đồ cột kép so sánh với bảng thống kê xem có chính xác không.
c) Tính tổng diện tích ba loại đất của Hà Nội.
d) Tính tỉ số phần trăm diện tích đất ở với diện tích đất sản xuất nông nghiệp của Hải Dương.
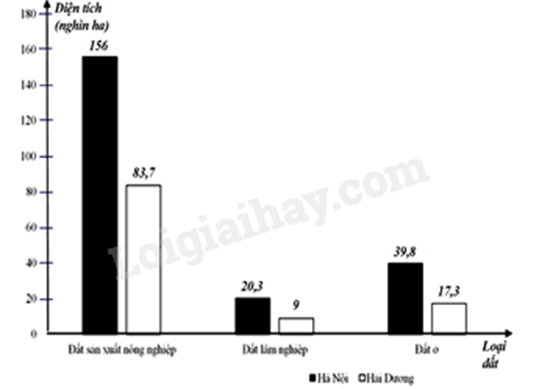
a) Sai
Loại đất là dữ liệu được biểu diễn bằng từ: đất sản xuất nông nghiệp, đất lâm nghiệp, đất ở nên là dữ liệu định tính.
b) Đúng
Từ biểu đồ cột kép ta có bảng thống kê:

c) Đúng
Tổng diện tích các loại đất của Hà Nội là:
156 + 20,3 + 39,8 = 216,1 (nghìn ha).
d) Đúng
Diện tích đất ở của Hải Dương so với diện tích đất sản xuất nông nghiệp là:
17,3.10083,7%≈20,67%.
Đáp án: SĐĐĐ
Cho tam giác ABC vuông tại A có AB = 6cm. AC = 8cm. M, N là trung điểm của AB , AC. Vẽ AD là tia phân giác của góc A trong tam giác ABC (D thuộc BC).
a) BC = 10cm.
b) MN = 4cm.
c) BD≈4,5cm.
d) BD.AN=AM.DC.
a) BC = 10cm.
b) MN = 4cm.
c) BD≈4,5cm.
d) BD.AN=AM.DC.
a) Áp dụng định lí Pythagore vào tam giác ABC để tính BC.
b) Chứng minh MN là đường trung bình để tính MN.
c) Áp dụng tính chất đường phân giác trong tam giác để tính BD.
d) Kết hợp tính chất đường phân giác trong tam giác và tính chất của trung điểm của AB, AC để kiểm tra khẳng định.
a) Đúng
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
BC=√AB2+AC2=√62+82=10(cm)
b) Sai
Vì M, N là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC.
Suy ra MN=12BC=5(cm)
c) Sai
Áp dụng tính chất đường phân giác trong tam giác ABC, ta có:
BDAB=CDACBDAB=BC−BDACBD6=10−BD88BD=6(10−BD)8BD=60−6BD14BD=60BD=6014≈4,3(cm)
d) Đúng
Theo tính chất đường phân giác trong tam giác ABC, ta có: BDAB=CDAC
Kết hợp với AB=2AM,AC=2AN (vì M, N là trung điểm của AB, AC), ta được:
BD2AM=CD2AN, suy ra 2AN.BD=2AM.CD
Do đó AN.BD=AM.CD (chia cả hai vế cho 2).
Đáp án: ĐSSĐ
Thống kê số lớp của 4 trường THCS trong 1 huyện năm học 2022-2023, được cho trong bảng sau:

Số lớp của trường THCS A và THCS B chiếm khoảng bao nhiêu % tổng số lớp của 4 trường THCS trong huyện? (làm tròn đến hàng đơn vị)
Đáp án:
Đáp án:
Xác định số lớp của trường THCS A và B.
Số lớp của cả 4 trường.
Tính tỉ số phần trăm của trường THCS A và THCS B so với tổng số lớp của 4 trường THCS trong huyện.
Tổng số lớp của trường THCS A và THCS B là: 24 + 20 = 44 (lớp)
Tổng số lớp của 4 trường THCS trong huyện là: 24 + 20 + 28 + 18 = 90 (lớp)
Số lớp của trường THCS A và THCS B chiếm số phần trăm so với tổng số lớp của 4 trường THCS trong huyện là: 44.10090%≈49%
Đáp án: 49
Biểu đồ sau cho biết cơ cấu GDP của Việt Nam năm 2022 (Nguồn: Tổng cục Thống kê).
Dựa vào biểu đồ, em hãy cho biết lĩnh vực đóng góp nhiều nhất vào GDP của Việt Nam năm 2022 với bao nhiêu phần trăm?
Đáp án:
Đáp án:
Từ biểu đồ xác định lĩnh vực đóng góp nhiều nhất.
Vì 41,3 > 38,2 > 11,9 > 8,6 nên lĩnh vực đóng góp nhiều nhất vào GDP của Việt Nam năm 2022 là Dịch vụ với 41,3%.
Đáp án: 41,3
Cho tam giác ABC, đường trung tuyến AD. Gọi M là một điểm trên cạnh AC sao cho AM=12MC. Gọi O là giao điểm của BM và AD. BM bằng bao nhiêu lần OM.
Đáp án:
Đáp án:
Qua D vẽ một đường thẳng song song với BM cắt AC tại N.
Dựa vào định lí đường trung bình của tam giác để chứng minh MN=NC=12MC, AM=MN=12MC.
Từ đó chứng minh OM là đường trung bình của tam giác ΔAND nên OM=12DN.
DN là đường trung bình của ΔMBC nên DN=12BM.
Kết hợp lại để tính được BM bằng bao nhiêu lần OM.
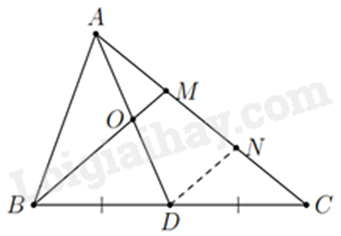
Qua D vẽ một đường thẳng song song với BM cắt AC tại N.
Xét ΔMBC có DB=DC và DN∥BM nên MN=NC=12MC (định lí đường trung bình của tam giác).
Mặt khác AM=12MC (gt), do đó AM=MN=12MC.
Xét ΔAND có AM=MN và BM∥DN nên OA=OD hay O là trung điểm của AD.
Xét ΔAND có:
M là trung điểm của AN (AM = MN), O là trung điểm của AD
nên OM là đường trung bình nên OM=12DN.(1)
Xét ΔMBC có:
N là trung điểm của CM (CN = MN)
D là trung điểm của BC (gt)
nên DN là đường trung bình nên DN=12BM.(2)
Từ (1) và (2) ta có: OM=12DN=12.(12BM)=14BM nên BM=4OM.
Đáp án: 4
Bạn An gieo một con xúc xắc 50 lần và thống kê kết quả các lần gieo ở bảng sau:

Xác suất thực nghiệm của biến cố “Gieo được mặt 4 chấm” là bao nhiêu?
Đáp án:
Đáp án:
Tính xác suất thực nghiệm:

Xác suất thực nghiệm của biến cố “Gieo được mặt 4 chấm” là:
1250=0,24.
Đáp án: 0,24
Biểu đồ dưới đây cho biết nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.
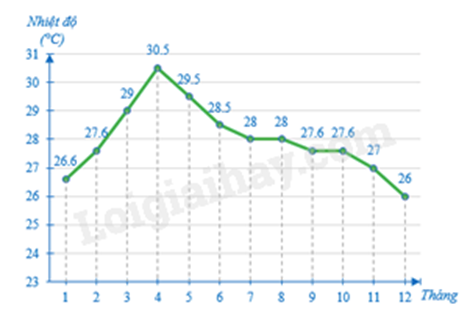
a) Lập bảng thống kê cho biểu đồ trên.
b) Tính độ chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất tại Thành phố Hồ Chí Minh năm 2020.
a) Quan sát biểu đồ đoạn thẳng để lập bảng thống kê tương ứng.
b) Xác định nhiệt độ cao nhất, nhiệt độ thấp nhất.
Độ chênh lệch = nhiệt độ cao nhất – nhiệt độ thấp nhất.
a) Bảng thống kê nhiệt độ trung bình các tháng năm 2020 tại Thành phố Hồ Chí Minh.

b) Nhiệt độ cao nhất: 30,5 (0C); Nhiệt độ thấp nhất: 26 (0C)
Độ chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất tại Thành phố Hồ Chí Minh năm 2020:
30,5 – 26 = 4,5 (0C)
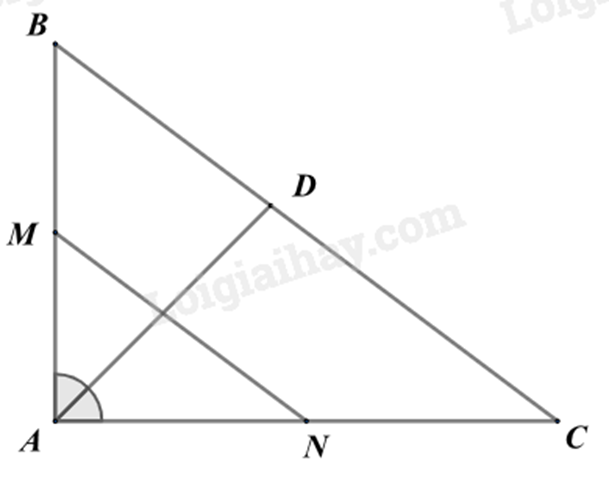
a) Cho tam giác ABC có AB = 6 cm, AC = 8 cm. Đường phân giác của góc A cắt BC tại D. Biết DB = 3 cm. Tính DC.
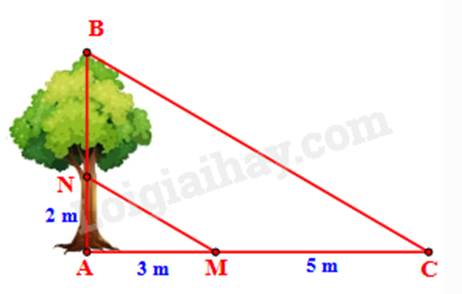
b) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong hình vẽ bên. Tìm chiều cao AB của cây.
a) Sử dụng tính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
b) Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
a)
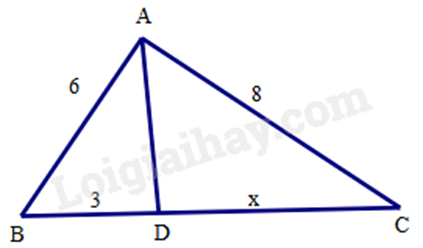
Theo tính chất của đường phân giác, ta có:
ABBD=ACCD63=8xx=8.36=4
b) Vì tia nắng chiếu song song nên MN // BC.
Áp dụng định lí Thalès với MN // BC, ta có:
ANNB=AMMC2NB=35NB=103
Chiều cao AB của cây là: AB=AN+NB=2+103=163(m)
Vậy chiều cao AB của cây là 163m.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365