Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 5. Tính chất tia phân giác của một góc
Lý thuyết tính chất ba đường phân giác của một góc
Trả lời câu hỏi 1 Bài 5 trang 68 SGK Toán 7 Tập 2 Trả lời câu hỏi 2 Bài 5 trang 69 SGK Toán 7 Tập 2 Trả lời câu hỏi 3 Bài 5 trang 69 SGK Toán 7 Tập 2 Bài 31 trang 70 SGK Toán 7 tập 2 Bài 32 trang 70 SGK Toán 7 tập 2 Bài 33 trang 70 SGK Toán 7 tập 2 Bài 34 trang 71 SGK Toán 7 tập 2 Bài 35 trang 71 SGK Toán 7 tập 2 Đề kiểm tra 15 phút - Đề số 1 - Bài 5, 6 - Chương 3 – Hình học 7 Đề kiểm tra 15 phút - Đề số 2 - Bài 5, 6 - Chương 3 – Hình học 7 Đề kiểm tra 15 phút - Đề số 3 - Bài 5, 6 - Chương 3 – Hình học 7 Đề kiểm tra 15 phút - Đề số 4 - Bài 5, 6 - Chương 3 – Hình học 7 Đề kiểm tra 15 phút - Đề số 6 - Bài 5, 6 - Chương 3 – Hình học 7 Đề kiểm tra 15 phút - Đề số 7 - Bài 5, 6 - Chương 3 – Hình học 7 Đề kiểm tra 15 phút - Đề số 8 - Bài 5, 6 - Chương 3 – Hình học 7Lý thuyết tính chất ba đường phân giác của một góc
A Kiến thức cơ bản
I. Kiến thức cơ bản
1. Định lí 1 (thuận)
Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó
GT : M∈Oz là tia phân giác của ^xOy
MA⊥Ox;MB⊥Oy
KL: MA=MB
2. Định lý 2 (đảo)
Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên phân giác của góc đó.
GT : M ở trong ^xOy
MA⊥Ox;MB⊥Oy
MA=MB
KL: OM là tia phân giác của ^xOy
Nhận xét:
Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
3. Tính chất ba đường phân giác của tam giác
Định lí 1: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường trung tuyến của tam giác đó.
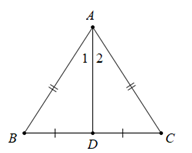
ΔABC: AB=AC^A1=^A2}⇒BD=DC
Định lí 2: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.

Tam giác ABC (hình vẽ) có ba đường phân giác giao nhau tại I. Khi đó
ˆA1=ˆA2,ˆB1=ˆB2,ˆC1=ˆC2.ID=IE=IF
II. Các dạng toán thường gặp
Dạng 1: Chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau
Phương pháp:
Sử dụng các tính chất:
+ Ta sử dụng định lý: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó
M∈OzMA⊥Ox;MB⊥Oy}⇒MA=MB
+ Giao điểm của hai đường phân giác của hai góc trong một tam giác nằm trên đường phân giác của góc thứ ba
+ Giao điểm các đường phân giác của tam giác cách đều ba cạnh của tam giác.
Dạng 2: Chứng minh hai góc bằng nhau
Phương pháp:
Ta sử dụng định lý: Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Dạng 3: Chứng minh tia phân giác của một góc
Phương pháp:
Ta sử dụng một trong các cách sau:
- Sử dụng định lý: Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
- Sử dụng định nghĩa phân giác
- Chứng minh hai góc bằng nhau nhờ hai tam giác bằng nhau
Dạng 4: Bài toán về đường phân giác với các tam giác đặc biệt (tam giác cân, tam giác đều)
Phương pháp:
Ta sử dụng định lý: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường trung tuyến của tam giác đó.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365