Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 15. Giới hạn của dãy số Toán 11 kết nối tri thức
Lý thuyết Giới hạn của dãy số - SGK Toán 11 Kết nối tri thức
Giải mục 1 trang 105, 106 SGK Toán 11 tập 1 - Kết nối tri thức Giải mục 2 trang 106,107 SGK Toán 11 tập 1 - Kết nối tri thức Giải mục 3 trang 107, 108 SGK Toán 11 tập 1 - Kết nối tri thức Giải mục 4 trang 108, 109 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.1 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.2 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.3 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.4 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.5 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức Bài 5.6 trang 109 SGK Toán 11 tập 1 - Kết nối tri thứcLý thuyết Giới hạn của dãy số - SGK Toán 11 Kết nối tri thức
1, Giới hạn hữu hạn của dãy số
1, Giới hạn hữu hạn của dãy số
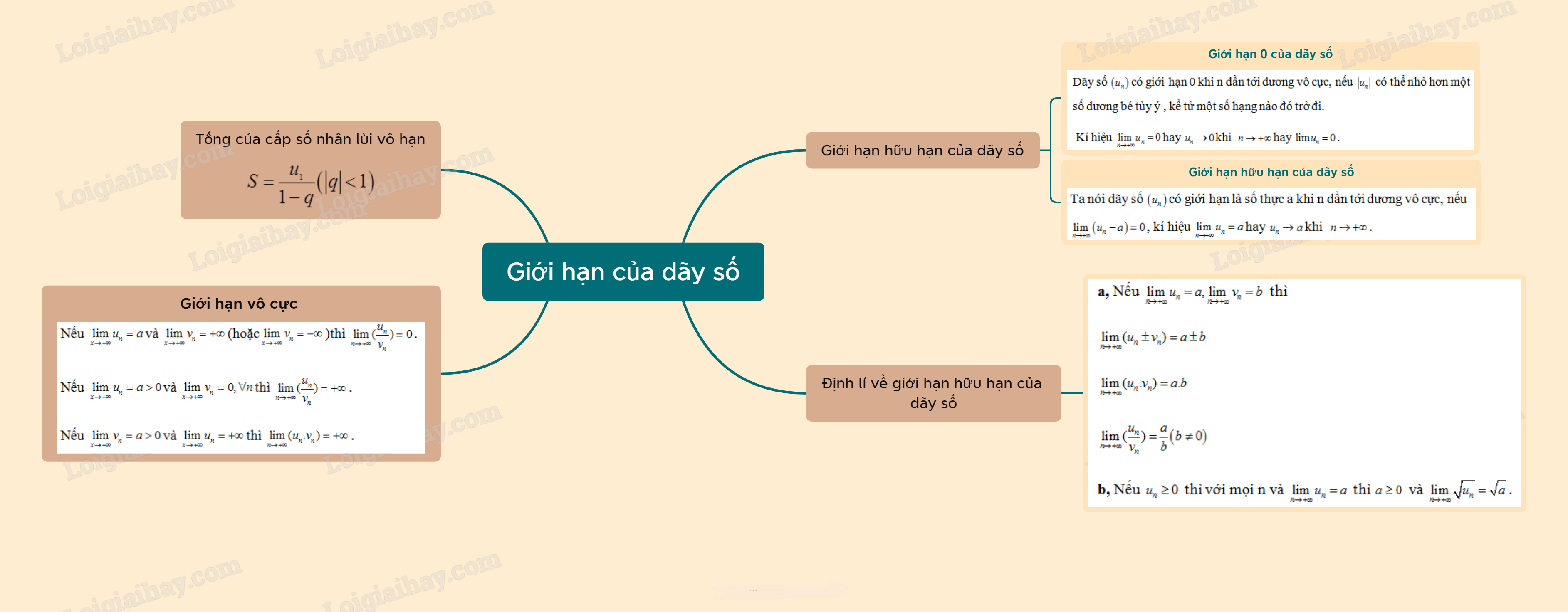
Ta nói dãy số (un) có giới hạn 0 khi n dần tới dương vô cực, nếu |un| có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi, kí hiệu lim hay {u_n} \to 0 khi n \to + \infty .
Ta nói dãy số \left( {{u_n}} \right) có giới hạn là số thực a khi n dần tới dương vô cực, nếu \mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - a} \right) = 0, kí hiệu \mathop {\lim }\limits_{n \to + \infty } {u_n} = a hay {u_n} \to a khi n \to + \infty .
* Chú ý: Nếu {u_n} = c (c là hằng số) thì \mathop {\lim }\limits_{n \to + \infty } {u_n} = c
2. Định lí về giới hạn hữu hạn của dãy số
a, Nếu \mathop {\lim }\limits_{n \to + \infty } {u_n} = a,\mathop {\lim }\limits_{n \to + \infty } {v_n} = b thì
\mathop {\lim }\limits_{n \to + \infty } ({u_n} \pm {v_n}) = a \pm b
\mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = a.b
\mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = \frac{a}{b}\left( {b \ne 0} \right)
b, Nếu {u_n} \ge 0 thì với mọi n và \mathop {\lim }\limits_{n \to + \infty } {u_n} = a thì a \ge 0 và \mathop {\lim }\limits_{n \to + \infty } \sqrt {{u_n}} = \sqrt a .
3. Tổng của cấp số nhân lùi vô hạn
S = \frac{{{u_1}}}{{1 - q}}\left( {\left| q \right| < 1} \right)
4. Giới hạn vô cực của dãy số
Dãy số \left( {{u_n}} \right) được gọi là có giới hạn + \infty khi n \to + \infty nếu {u_n} có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu \mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty hay {u_n} \to + \infty khi n \to + \infty .
Dãy số \left( {{u_n}} \right) được gọi là có giới hạn - \infty khi n \to + \infty nếu \mathop {\lim }\limits_{x \to + \infty } \left( { - {u_n}} \right) = + \infty , kí hiệu \mathop {\lim }\limits_{x \to + \infty } {u_n} = - \infty hay {u_n} \to - \infty khi n \to + \infty .
*Quy tắc:
Nếu \mathop {\lim }\limits_{x \to + \infty } {u_n} = a và \mathop {\lim }\limits_{x \to + \infty } {v_n} = + \infty (hoặc\mathop {\lim }\limits_{x \to + \infty } {v_n} = - \infty ) thì \mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = 0.
Nếu \mathop {\lim }\limits_{x \to + \infty } {u_n} = a > 0 và \mathop {\lim }\limits_{x \to + \infty } {v_n} = 0,\forall n thì \mathop {\lim }\limits_{n \to + \infty } (\frac{{{u_n}}}{{{v_n}}}) = + \infty .
Nếu \mathop {\lim }\limits_{x \to + \infty } {v_n} = a > 0 và \mathop {\lim }\limits_{x \to + \infty } {u_n} = + \infty thì \mathop {\lim }\limits_{n \to + \infty } ({u_n}.{v_n}) = + \infty .
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365