Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 3. Hai mặt phẳng vuông góc Toán 11 Chân trời sáng tạo
Giải mục 3 trang 67, 68, 69 SGK Toán 11 tập 2 - Chân trời sáng tạo
Giải mục 4 trang 69, 70, 71 SGK Toán 11 tập 2 - Chân trời sáng tạo Giải mục 5 trang 71, 72, 73 SGK Toán 11 tập 2 - Chân trời sáng tạo Bài 1 trang 73 SGK Toán 11 tập 2 – Chân trời sáng tạo Bài 2 trang 73 SGK Toán 11 tập 2 – Chân trời sáng tạo Bài 3 trang 73 SGK Toán 11 tập 2 – Chân trời sáng tạo Bài 4 trang 74 SGK Toán 11 tập 2 – Chân trời sáng tạo Bài 5 trang 74 SGK Toán 11 tập 2 – Chân trời sáng tạo Bài 6 trang 74 SGK Toán 11 tập 2 – Chân trời sáng tạo Giải mục 2 trang 66, 67 SGK Toán 11 tập 2 - Chân trời sáng tạo Giải mục 1 trang 65 SGK Toán 11 tập 2 - Chân trời sáng tạo Lý thuyết Hai mặt phẳng vuông góc - Toán 11 Chân trời sáng tạoGiải mục 3 trang 67, 68, 69 SGK Toán 11 tập 2 - Chân trời sáng tạo
Cho đường thẳng (a) vuông góc với mặt phẳng (left( Q right)).
Hoạt động 4
Cho đường thẳng vuông góc với mặt phẳng . Mặt phẳng chứa và cắt theo giao tuyến . Trong ta vẽ đường thẳng vuông góc với .
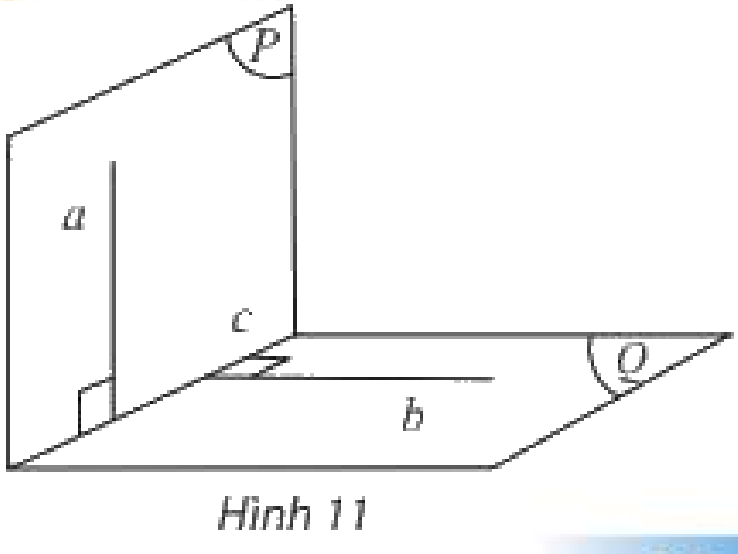
Hỏi:
a) có vuông góc với không?
b) Đường thẳng vuông góc với không?
Hoạt động 5
Cho hai mặt phẳng và cùng vuông góc với mặt phẳng . Gọi là giao tuyến của và . Lấy điểm trong , vẽ hai đường thẳng và lần lượt vuông góc với và . Hỏi:
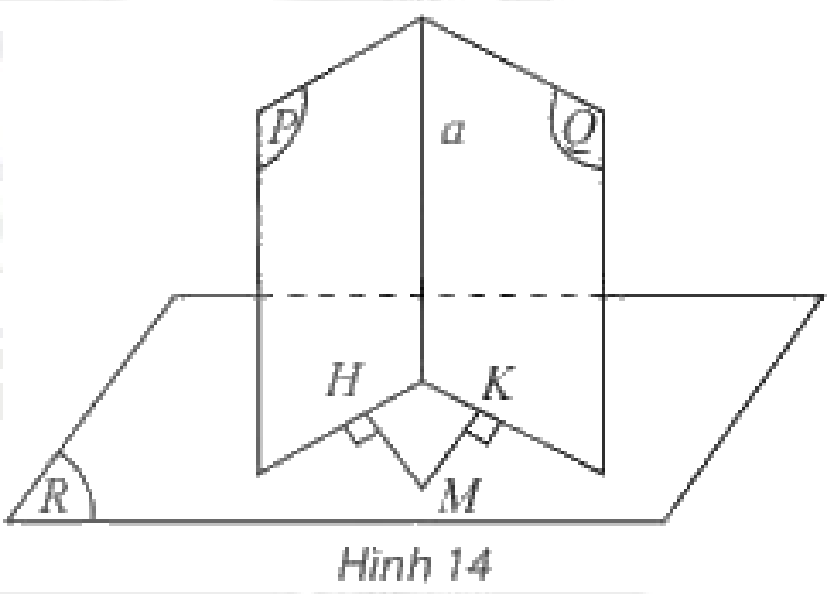
a) Hai đường thẳng và có nằm trong không?
b) Đường thẳng có vuông góc với không?
Thực hành 2
Tứ diện có . Trong tam giác vẽ đường cao và cắt nhau tại . Trong mặt phẳng vẽ vuông góc với tại . Gọi là trực tâm của tam giác . Chứng minh rằng:
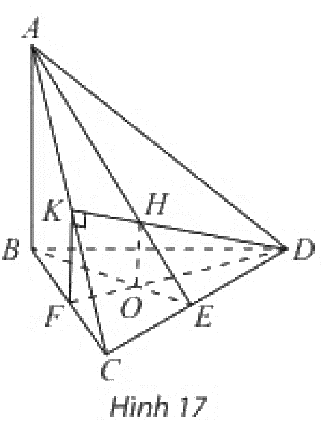
a) và ;
b) .
Vận dụng 2
Nêu cách đặt một quyển sách lên mặt bàn sao cho tất cả các trang sách đều vuông góc với mặt bàn.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365