Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 1 Toán 8 - Kết nối tri thức
Đề thi học kì 1 Toán 8 - Đề số 2 - Kết nối tri thức
Đề thi học kì 1 Toán 8 - Đề số 3 - Kết nối tri thức Đề thi học kì 1 Toán 8 - Đề số 4 - Kết nối tri thức Đề thi học kì 1 Toán 8 - Đề số 5 - Kết nối tri thức Đề thi học kì 1 Toán 8 Kết nối tri thức - Đề số 6 Đề thi học kì 1 Toán 8 Kết nối tri thức - Đề số 7 Đề thi học kì 1 Toán 8 Kết nối tri thức - Đề số 8 Đề thi học kì 1 Toán 8 - Đề số 1 - Kết nối tri thức Đề cương ôn tập học kì 1 Toán 8 - Kết nối tri thứcĐề thi học kì 1 Toán 8 - Đề số 2 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Câu 1: Thu gọn đa thức (2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y) ta được:
Thu gọn đa thức 2x4y−4y5+5x4y−7y5+x2y2−2x4y ta được:
Đáp án : D
Sử dụng quy tắc tính với đa thức.
Ta có:
2x4y−4y5+5x4y−7y5+x2y2−2x4y=(2x4y+5x4y−2x4y)+(−4y5−7y5)+x2y2=5x4y−11y5+x2y2
Đa thức x5+4x3−6x2 chia hết cho đơn thức nào?
Đáp án : D
Dựa vào quy tắc chia đa thức cho đơn thức.
Đa thức chia hết cho một đơn thức nếu các hạng tử của đa thức đó chia hết cho đơn thức.
Vì vậy bậc của các biến đơn thức phải không lớn hơn bậc của các biến trong đa thức.
Đa thức x5+4x3−6x2 là đa thức biến x với bậc nhỏ nhất của biến x là 2 nên A, B, C không thỏa mãn. (4xy có biến y; 6x3 có bậc của x là 3; x5 có bậc của x là 5).
Vậy đa thức x5+4x3−6x2 chia hết cho đơn thức 4x2.
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
a. (x+y)(x2+xy+y2)
b. (x−y)(x2+xy+y2)
c. (x+y)(x2−xy+y2)
1. x3+y3
2. x3+2x2y+2xy2+y3
3. x3−y3.
a. (x+y)(x2+xy+y2)
2. x3+2x2y+2xy2+y3
b. (x−y)(x2+xy+y2)
3. x3−y3.
c. (x+y)(x2−xy+y2)
1. x3+y3
Sử dụng kiến thức về các hằng đẳng thức đáng nhớ.
a. (x+y)(x2+xy+y2)
=x3+x2y+x2y+xy2+y2x+y3=x3+2x2y+2xy2+y3
⇒ a – 2.
b. (x−y)(x2+xy+y2)=x3−y3⇒ b – 3.
c. (x+y)(x2−xy+y2)=x3+y3⇒ c – 1.
Hình thang cân là hình thang
Đáp án : D
Sử dụng khái niệm hình thang cân.
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự ở E và F. Tam giác ABC cần thêm điều kiện gì thì AEDF là chữ nhật?
Đáp án : B
Sử dụng dấu hiệu nhận biết hình vuông.
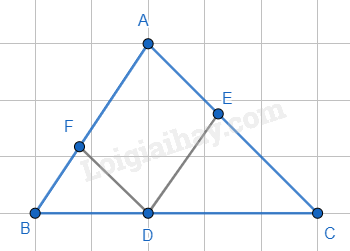
Vì DE // AF; DF // AE (gt) => AEDF là hình bình hành.
Để hình bình hành AEDF là hình chữ nhật thì ˆA=900 hay tam giác ABC vuông tại A.
Cho tam giác ABC vuông tại A có AB = 12BC, đường trung tuyến AM. Tam giác ABM là tam giác gì?
Đáp án : C
Dựa vào kiến thức về đường trung tuyến ứng với cạnh huyền trong tam giác vuông.
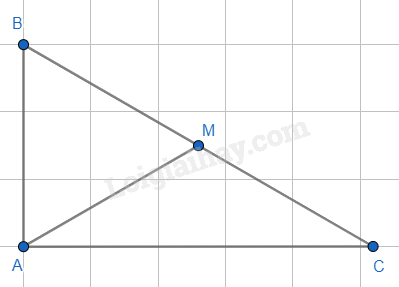
Ta có tam giác ABC vuông tại A, AM là đường trung tuyến nên AM = 12BC = BM = MC.
Mà AB = 12BC (gt)
=> AM = AB = BM hay tam giác ABM đều.
Viết tỉ số cặp đoạn thằng có độ dài như sau: AB = 4dm; CD = 20dm.
Đáp án : B
Sử dụng kiến thức về tỉ số của hai đoạn thẳng.
Ta có: ABCD=420=15.
Tìm giá trị của x trong hình vẽ?
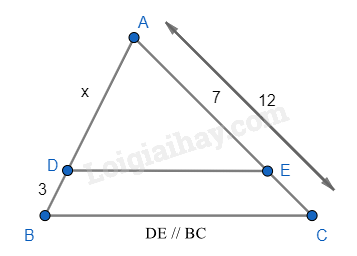
Đáp án : A
Áp dụng định lí Thalès để tính x.
Vì DE // BC nên ADAB=AEAC⇔xx+3=712
⇔12x=7(x+3)⇔12x=7x+21⇔12x−7x=21⇔5x=21⇔x=215
Cho ΔABC, AD là tia phân giác trong của góc A. Hãy chọn câu đúng.
Đáp án : B
Sử dụng tính chất của đường phân giác trong tam giác.
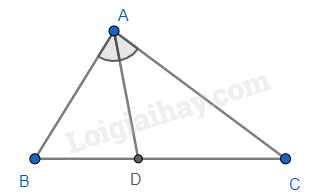
Theo tính chất của đường phân giác trong tam giác, ta có: ABDB=ACDC nên B đúng.
Một số con vật sống trên cạn: Cá voi, chó, mèo , bò. Trong các dữ liệu trên, dữ liệu chưa hợp lí là:
Đáp án : A
Xác định xem con vật nào không sống trên cạn.
Dữ liệu chưa hợp lí là cá voi, vì cá voi không sống trên cạn.
Trong cuộc khảo sát tìm hiểu về cách học của học sinh khối 8 được kết quả như sau:

Có 50 % học sinh học qua đọc, viết.
Có 35 % học sinh học qua nghe
Có 10 % học sinh học qua vận động.
Có 5 % học sinh học qua quan sát.
Khẳng định nào sau đây là đúng?
Đáp án : C
Dựa vào phân loại dữ liệu.
Các hình thức học: đọc viết; nghe; vận động; quan sát không phải là số.
Số lượng học sinh có cách học qua đọc, viết; nghe; vận động; quan sát lần lượt là: 50%, 30%, 10%, 5% là số liệu.
Vậy chọn đáp án C.
Phân tích các đa thức sau thành nhân tử:
a) 2x2+6x
b) x4+3x3+x+3
c) 64−x2−y2+2xy
Sử dụng các phương pháp phân tích đa thức thành nhân tử.
a) 2x2+6x=2x(x+3)
b) x4+3x3+x+3=(x4+x)+(3x3+3)
=x(x3+1)+3(x3+1)=(x+3)(x3+1)=(x+3)(x+1)(x2−x+1)
c) 64−x2−y2+2xy
=64−(x2+y2−2xy)=82−(x−y)2=(8−x+y)(8+x−y)
a) Rút gọn biểu thức sau:
A=(x+5)(x+1)+(x−2)(x2+2x+4)−x(x2+x−2)
b) Tính nhanh: 742 + 242 – 48.74.
Dựa vào các phép tính với đa thức, các hằng đẳng thức để rút gọn A.
a) Ta có:
A=(x+5)(x+1)+(x−2)(x2+2x+4)−x(x2+x−2)=(x2+5x+x+5)+(x3−23)−(x3+x2−2x)=x2+6x+5+x3−8−x3−x2+2x=(x3−x3)+(x2−x2)+(6x+2x)+(5−8)=8x−3
b) 742 + 242 – 48.74 = 7422 + 242 – 2.24.74 = (74 – 24)2 = 502 = 2 500.
Biểu đồ đoạn thẳng biểu diễn vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta qua các năm 2015; 2017; 2018; 2019; 2020. (đơn vị: nghìn tỷ đồng)
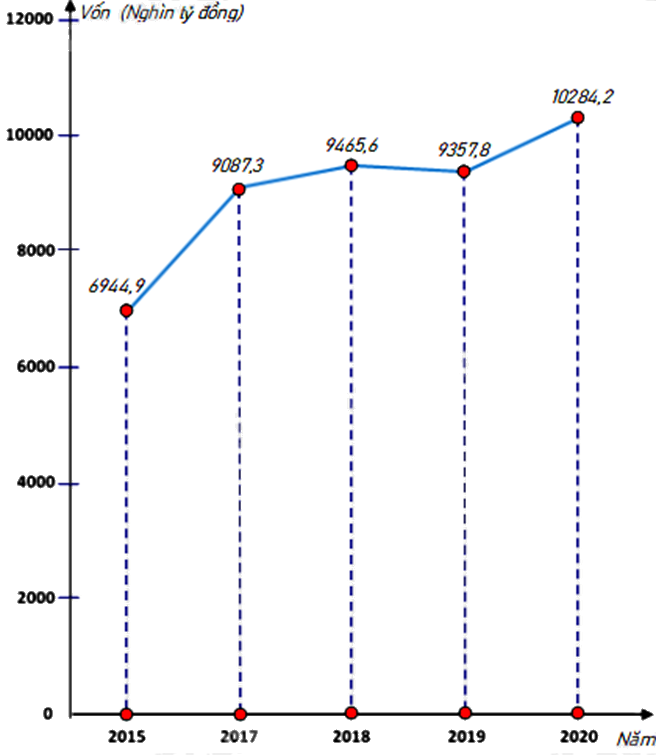
(Nguồn: Niên giám thống kê 2021)
a) Lập bảng thống kê vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta qua các năm 2015; 2017; 2018; 2019; 2020 theo mẫu sau:
|
Năm |
2015 |
2017 |
2018 |
2019 |
2020 |
|
Vốn (nghìn tỷ đồng) |
? |
? |
? |
? |
? |
b) Năm nào vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta là nhiều nhất? ít nhất?
c) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười)?
d) Năm 2017 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước giảm bao nhiêu phần trăm so năm 2019 (làm tròn kết quả đến hàng phần mười)?
Dựa vào biểu đồ để trả lời câu hỏi.
a)
|
Năm |
2015 |
2017 |
2018 |
2019 |
2020 |
|
Vốn (nghìn tỷ đồng) |
6944,9 |
9087,3 |
9465,6 |
9357,8 |
10284,2 |
b) Vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta nhiều nhất là năm 2020; ít nhất là năm 2015.
c) Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước năm 2020 so với năm 2015 là: 10284,26944,9.100%=148,1%
Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng 148,1% - 100% = 48,1% so năm 2015.
d) Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước năm 2017 so với năm 2019 là 9087,39357,8.100%=97,1%
Năm 2017 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước giảm 100% - 97,1% = 2,9% so năm 2019.
1. Giữa hai điểm B và C bị ngăn cách bởi hồ nước (như hình dưới). Hãy xác định độ dài BC mà không cần phải bơi qua hồ. Biết rằng đoạn thẳng KI dài 30m và K là trung điểm của AB, I là trung điểm của AC.
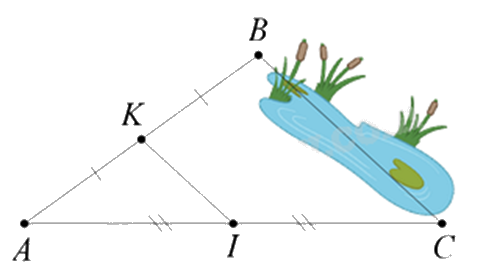
2. Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi H là điểm đối xứng với M qua AB, E là giao điểm của MH và AB. Gọi K là điểm đối xứng với M qua AC, F là giao điểm của MK và AC.
a) Các tứ giác AEMF, AMBH, AMCK là hình gì? Vì sao?
b) Chứng minh rằng H đối xứng với K qua A.
c) Tam giác vuông ABC cần thêm điều kiện gì thì tứ giác AEMF là hình vuông?
a) Tứ giác AEMF là hình chữ nhật. Các tứ giác AMBH, AMCK là hình thoi.
b) Theo a) suy ra HA∥BC, AK∥MC ⇒ H, A, K thẳng hàng. Lại có AH=AM=AK ⇒ H, K đối xứng với nhau qua A.
c) Để hình chữ nhật AEMF là hình vuông thì cần thêm điều kiện AE=EM. ⇒ AB=AC. Vậy tam giác ABC vuông cân tại A.
1.
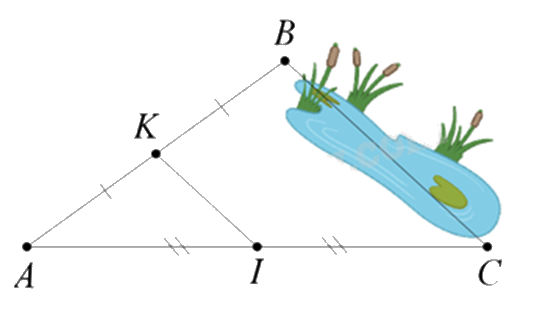
Vì K là trung điểm của AB, I là trung điểm của AC nên KI là đường trung bình của tam giác ABC => KI // BC và KI = 12BC.
Vì KI = 30 m nên BC = 2.KI = 2.30 = 60 m.
Vậy BC = 60 m.
2.
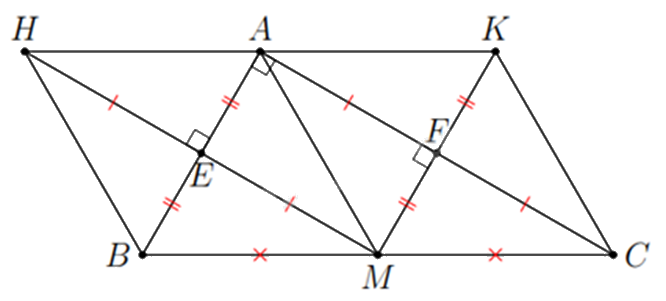
a) Ta có: H là điểm đối xứng với M qua AB, E là giao điểm của MH và AB => AB⊥HM(ˆE=900) và HE = EM.
K là điểm đối xứng với M qua AC, F là giao điểm của MK và AC=> AC⊥MK(ˆF=900) và MF = FK.
Tứ giác AEMF có: ˆA=ˆE=ˆF=900 (cmt) nên AEMF là hình chữ nhật (đpcm). Suy ra ME // AF; MF // AE.
Ta có: M là trung điểm của BC (vì AM là đường trung tuyến), ME // AC (cmt); MF // AE (cmt) => ME và MF là đường trung bình của tam giác ABC. => ME = 12AC; MF = 12AB. (1)
Mà ME = AF; MF = AE (vì AEMF là hình chữ nhật) (2)
Từ (1) và (2) suy ra AE = EB = 12AB; AF = FC = 12AC.
Xét tứ giác AMBH có: AE = EB; HE = EM và AB⊥HM tại E nên AMBH là hình thoi (đpcm).
Tương tự, tứ giác AMCK có: AF = FC; MF = FK và AC⊥MK tại F nên AMCK là hình thoi (đpcm).
b) Xét tứ giác BHKC có: BH // CK và BH = CK (cùng song song và bằng AM) nên BHKC là hình bình hành => BC // HK.
Vì AMBH và AMCK là hình thoi nên HA // BM, HA = BM; AK // CM, AK = CM.
Ta có BC // HK, BC // HA; BC // AK (cmt) => H, A, K thẳng hàng.
Mà AH = AK = BM = MC (vì M là trung điểm của BC) nên H đối xứng với K qua A.
c) Để AEMF là hình vuông thì AE = AF ⇔ 12AB=12AC hay AB = AC ⇔ tam giác ABC vuông cân tại A.
Vậy để AEMF là hình vuông thì tam giác ABC phải là tam giác cân.
Chứng minh biểu thức A=−x2+23x−1 luôn luôn âm với mọi giá trị của biến
Sử dụng hằng đẳng thức để biến đổi biểu thức.
A=−x2+23x−1=−(x2−2x.13+19−19+1)=−[x2−2x.13+(13)2+89]=−[(x−13)2+89]=−(x−13)2−89
Ta có −(x−13)2≤0 nên −(x−13)2−89<0 với mọi x.
Vậy A < 0 hay luôn luôn âm với mọi giá trị x.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365