Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 1 Toán 8 - Kết nối tri thức
Đề thi học kì 1 Toán 8 Kết nối tri thức - Đề số 7
Đề thi học kì 1 Toán 8 Kết nối tri thức - Đề số 8 Đề thi học kì 1 Toán 8 Kết nối tri thức - Đề số 6 Đề thi học kì 1 Toán 8 - Đề số 5 - Kết nối tri thức Đề thi học kì 1 Toán 8 - Đề số 4 - Kết nối tri thức Đề thi học kì 1 Toán 8 - Đề số 3 - Kết nối tri thức Đề thi học kì 1 Toán 8 - Đề số 2 - Kết nối tri thức Đề thi học kì 1 Toán 8 - Đề số 1 - Kết nối tri thức Đề cương ôn tập học kì 1 Toán 8 - Kết nối tri thứcĐề thi học kì 1 Toán 8 Kết nối tri thức - Đề số 7
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Trong biểu thức (2x+5)2=4x2+...+25(2x+5)2=4x2+...+25, đơn thức còn thiếu tại … là
10x10x.
−10x−10x.
20x20x.
−20x−20x.
Đáp án : C
Sử dụng hằng đẳng thức bình phương của một tổng: (A+B)2=A2+2AB+B2(A+B)2=A2+2AB+B2.
Ta có: (2x+5)2=4x2+2.2x.5+25=4x2+20x+25(2x+5)2=4x2+2.2x.5+25=4x2+20x+25 nên đơn thức còn thiếu là 20x20x.
Đáp án C
Cho hình bên, biết DE//ACDE//AC, tìm xx
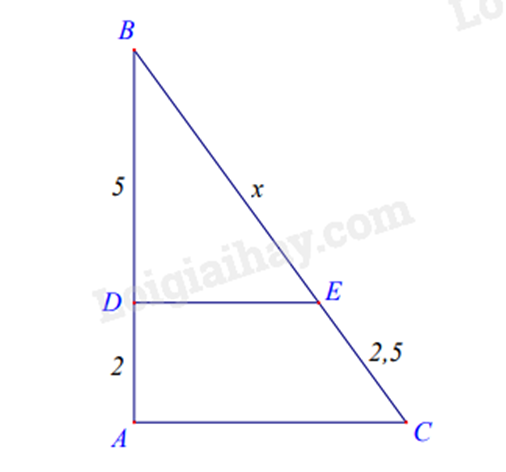
x=5x=5.
x=6,25x=6,25.
x=8x=8.
x=6,5x=6,5.
Đáp án : B
Áp dụng Định lí Thalès trong tam giác: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Vì DE // AC nên BDAD=BEECBDAD=BEEC hay 52=x2,552=x2,5, suy ra x=2,5.52=6,25x=2,5.52=6,25.
Đáp án B
Khai triển hằng đẳng thức 9x2−169x2−16 ta được kết quả là
(9x−4)(9x+4)(9x−4)(9x+4).
(3x−4)2(3x−4)2.
(3x+4)(3x−4)(3x+4)(3x−4).
(3x+4)2(3x+4)2.
Đáp án : C
Sử dụng hằng đẳng thức hiệu hai bình phương: A2−B2=(A−B)(A+B)A2−B2=(A−B)(A+B).
Ta có:
9x2−16=(3x)2−42=(3x−4)(3x+4)9x2−16=(3x)2−42=(3x−4)(3x+4).
Đáp án C
Cho hình vẽ, biết các số trên hình cùng đơn vị đo. Tỉ số xyxy bằng
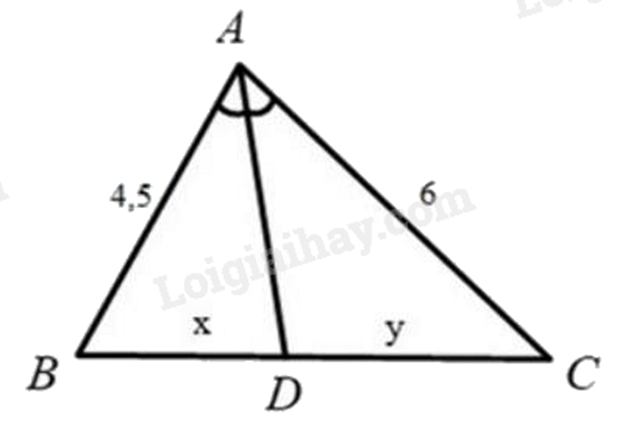
4343.
1313.
2323.
3434.
Đáp án : D
Sử dụng tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
Ta có AD là tia phân giác của góc A nên BDDC=ABACBDDC=ABAC hay xy=4,56=34xy=4,56=34.
Đáp án D
Tứ giác ABCD có số đo các góc ˆA=75∘;ˆB=60∘;ˆC=120∘ˆA=75∘;ˆB=60∘;ˆC=120∘. Số đo góc D bằng
50∘50∘.
110∘110∘.
105∘105∘.
360∘360∘.
Đáp án : C
Áp dụng định lí tổng các góc của một tứ giác bằng 360∘360∘.
Tứ giác ABCD có ˆA+ˆB+ˆC+ˆD=360∘ˆA+ˆB+ˆC+ˆD=360∘
Suy ra ˆD=360∘−(75∘+60∘+120∘)=360∘−255∘=105∘ˆD=360∘−(75∘+60∘+120∘)=360∘−255∘=105∘
Đáp án C
Thực hiện phép tính (5x6y5+8x2y3):4x2y được kết quả là
x4y4+4y2.
54x4y4−2xy2.
54x4y4+2y2.
134x6y7.
Đáp án : C
Sử dụng quy tắc chia đa thức cho đơn thức: Muốn chia đa thức A cho đơn thức B (trường hợp chia hết), ta chia từng hạng tử của A cho B rồi cộng các kết quả với nhau.
Ta có:
(5x6y5+8x2y3):4x2y=5x6y5:4x2y+8x2y3:4x2y=54x4y4+2y2
Đáp án C
Trong các dữ liệu sau, dữ liệu nào không phải là dữ liệu số?
Chiều cao trung bình của một số loại thân cây gỗ (đơn vị tính là mét): 7; 8; 9,3; ….
Quốc tịch của các học sinh trong một trường quốc tế: Việt Nam, Lào, Campuchia,….
Cân nặng của trẻ sơ sinh (đơn vị là gam): 4000, 2500, 5000,….
Số học sinh đeo kính trong một lớp học (đơn vị tính là học sinh): 20; 10; 15;.....
Đáp án : B
Xác định xem dữ liệu nào là số, dữ liệu nào không phải là số.
“Quốc tịch của các học sinh trong một trường quốc tế: Việt Nam, Lào, Campuchia,…” không được biểu diễn bằng số nên không phải là dữ liệu số.
Đáp án B
Thân nhiệt (∘C) của bạn An trong cùng khung giờ 7h sáng các ngày trong tuần được ghi lại trong bảng sau:

Bạn An đã thu được dữ liệu trên bằng cách nào?
Xem ti vi.
Ghi chép số liệu thống kê hằng ngày.
Thu thập từ các nguồn có sẵn như sách, báo,....
Lập bảng hỏi.
Đáp án : B
Xác định cách thu thập dữ liệu phù hợp.
Để thu thập thân nhiệt thì bạn An cần thực hiện đo nhiệt độ và ghi chép số liệu thống kê hằng ngày nên ta chọn đáp án B.
Đáp án B
Sau khi thu gọn đơn thức −3x3y.2y2 ta được:
−6x3y3.
6x3y3.
−6x2y3.
−6x3y2.
Đáp án : A
Áp dụng các tính chất của phép nhân và phép nâng lên lũy thừa để mỗi biến chỉ còn xuất hiện một lần.
Ta có: −3x3y.2y2=−(3.2).x3.(y.y2)=−6x3y3.
Đáp án A
Cho dãy dữ liệu sau: “Một số con vật sống trên cạn: cá voi, chó, mèo, ngựa”. Trong các dữ liệu trên, dữ liệu chưa hợp lí là:
Mèo.
Ngựa.
Chó.
Cá voi.
Đáp án : D
Xác định xem trong các con vật được kể tên, có con nào không sống trên cạn.
Dữ liệu chưa hợp lí là “cá voi” vì cá voi không sống trên cạn.
Đáp án D
Cho hình thang ABCD có AB // CD, hai đường chéo AC, BD cắt nhau tại O sao cho OA = OB, OC = OD. Tìm khẳng định sai trong các khẳng định sau?
AC = BD.
BC = AD.
ABCD là hình thang cân.
Tam giác AOD cân tại O.
Đáp án : D
Chứng minh tứ giác ABCD là hình thang cân và sử dụng tính chất của hình thang cần để xác định khẳng định sai.
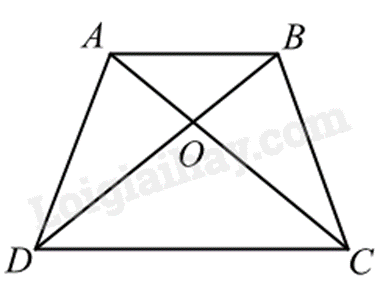
Vì hai đường chéo AC, BD cắt nhau tại O và OA = OB, OC = OD nên ta có:
OA + OC = OB + OD
suy ra AC = BD.
Hình thang ABCD (AB // CD) có AC = BD nên ABCD là hình thang cân. Do đó BC = AD.
Vậy đáp án A, B, C đúng.
Đáp án D sai.
Đáp án D
Cho tam giác ABC có I, K lần lượt là trung điểm của AB và AC. Biết BC = 10cm, độ dài IK là:
4cm.
5cm.
3,5cm.
10cm.
Đáp án : B
Dựa vào tính chất đường trung bình: Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.

Vì I, K lần lượt là trung điểm của AB và AC nên IK là đường trung bình của tam giác ABC, do đó IK=12BC=12.10=5(cm)
Đáp án B
Rút gọn rồi tính giá trị biểu thức A=(2x+1)(3x−5)−6x(x−1) tại x=2024.
Sử dụng quy tắc nhân đơn thức với đa thức, nhân đa thức với đa thức.
Sau đó thay x=2024 vào để tính giá trị.
Ta có:
A=(2x+1)(3x−5)−6x(x−1)=6x2+3x−10x−5−6x2+6x=(6x2−6x2)+(3x−10x+6x)−5=−x−5
Thay x=2024 vào A, ta được:
A=−2024−5=−2029
Phân tích các đa thức sau thành nhân tử:
a) 12x2+15x
b) x2−9y2+8x+16
a) Sử dụng phương pháp đặt nhân tử chung để phân tích.
b) Kết hợp phương pháp nhóm hạng tử và sử dụng hằng đẳng thức hiệu hai bình phương để phân tích.
a) 12x2+15x=3x(4x+5)
b) x2−9y2+8x+16
=(x2+8x+16)−9y2=(x+4)2−(3y)2=(x+4−3y)(x+4+3y)
Cho bảng thống kê dữ liệu về số cơn bão từ năm 2014 – 2018 như sau:

Lựa chọn và vẽ biểu đồ biểu diễn dữ liệu này. Nếu ta có dữ liệu về số cơn bão hằng năm trên toàn cầu từ năm 1970 đến nay thì ta nên dùng biểu đồ nào để biểu diễn dữ liệu?
Xác định biểu đồ phù hợp để biểu diễn dữ liệu.
Nếu muốn biểu diễn sự thay đổi của một đại lượng theo thời gian, ta dùng biểu đồ đoạn thẳng. Khi số lượng thời điểm quan sát ít, ta có thể biểu diễn bằng biểu đồ cột.
- Với bảng thống kê dữ liệu về số cơn bão từ năm 2014 – 2018, ta nên lựa chọn biểu đồ cột để biểu diễn.
Ta có biểu đồ biểu diễn dữ liệu sau:
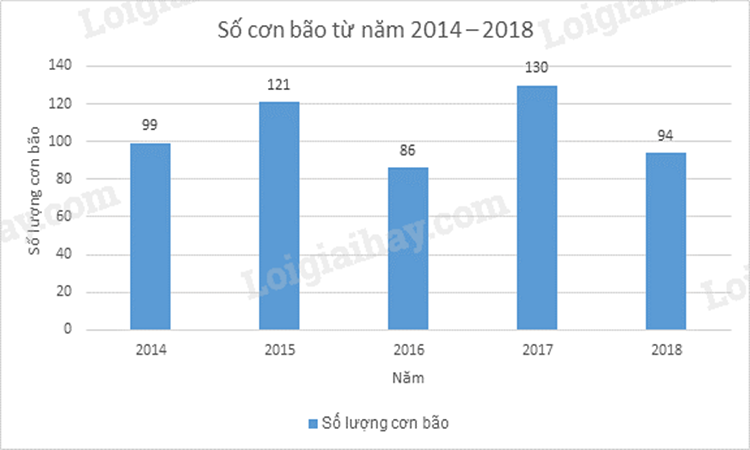
- Nếu ta có dữ liệu về số cơn bão hằng năm trên toàn cầu từ năm 1970 đến nay thì ta nên dùng biểu đồ đoạn thẳng để biểu diễn dữ liệu. Ta không nên sử dụng biểu đồ cột với số lượng năm lớn.
Cho tam giác ABC. Từ điểm D (D∈AB) kẻ đường thẳng song song với BC cắt AC tại E.
a) Cho AB = 15cm, AC = 20cm, AE = 8cm. Tính độ dài AD.
b) Qua E kẻ EM//CD(M∈AD). Chứng minh AD2=AM.AB.
a) Áp dụng định lí Thalès với DE // BC để tính AD.
b) Áp dụng định lí Thalès với EM // CD và DE // BC để chứng minh AD2=AM.AB.
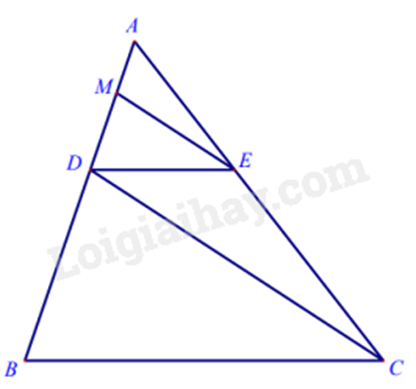
a) Xét tam giác ABC có DE // BC nên ADAB=AEAC (định lí Thalès)
hay AD15=820, suy ra AD=15.820=6.
b) Xét tam giác ADC có EM // CD nên AMAD=AEAC (định lí Thalès)
Mà ADAB=AEAC (cmt) nên AMAD=ADAB, suy ra AD2=AM.AB.
Giữa hai điểm A, B là một hồ nước sâu. Biết A, B lần lượt là trung điểm của MC, MD (xem hình vẽ).
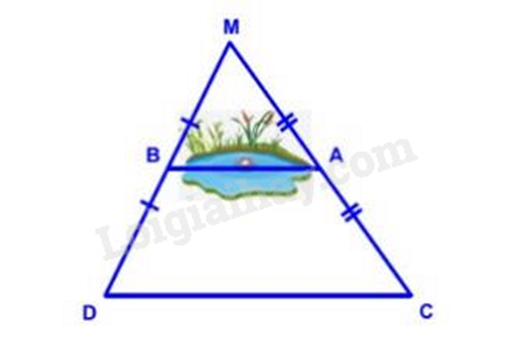
Bạn Mai đi từ C đến D với vận tốc 9,6km/h hết 1 phút 30 giây. Hỏi hai điểm A và B cách nhau bao nhiêu mét?
Đổi các số liệu về cùng đơn vị.
Tính độ dài đoạn CD theo công thức quãng đường = vận tốc . thời gian.
Chứng minh AB là đường trung bình của tam giác ADC, áp dụng tính chất đường trung bình để tính AB.
Đổi 9,6km/h = 9600m/h = 160m/phút.
1 phút 30 giây = 1,5 phút.
Khi đó độ dài đoạn CD chính là quãng đường bạn Mai với vận tốc 160m/phút trong 1,5 phút.
Độ dài đoạn CD là: 160.1,5 = 240 (m)
Vì A, B lần lượt là trung điểm của MC, MD nên AB là đường trung bình của tam giác ACD,
suy ra AB=12CD=12.240=120(m).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365