Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 1 Toán 12 - Chân trời sáng tạo
Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 1
Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 2 Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 3 Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 4 Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 5 Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 6 Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 7 Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 8Đề thi giữa kì 1 Toán 12 Chân trời sáng tạo - Đề số 1
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau:
Cho hàm số f(x) liên tục trên R có bảng biến thiên như sau: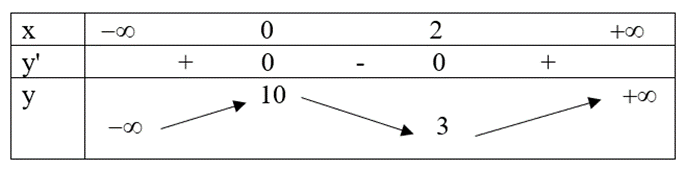
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
(−∞;0)(−∞;0)
(0;2)(0;2)
(2;+∞)(2;+∞)
R
Đáp án : B
Quan sát bảng biến thiên và nhận xét.
Quan sát bảng biến thiên thấy y’ < 0 trên khoảng (0;2) nên hàm số nghịch biến trên khoảng (0;2).
Đường cong dưới đây là đồ thị hàm số nào?
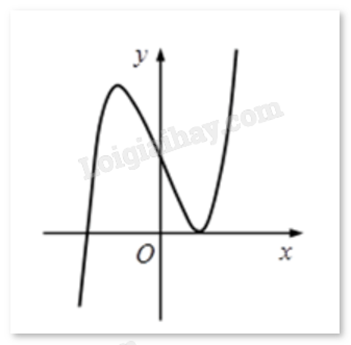
y=x3−3x+2
y=−x3−x2+1
y=x2+x+1
y=−x3−3x+2
Đáp án : A
Quan sát đồ thị và nhận xét.
Đồ thị có hai cực trị nên là hàm số bậc ba. Nhánh cuối của đồ thị đi lên nên a > 0.
Cho hàm số f(x) có đồ thị như hình dưới đây:
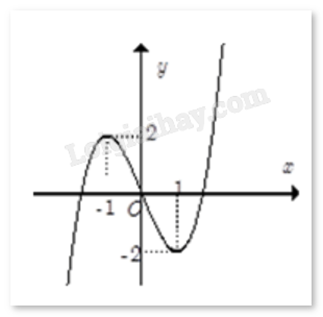
Giá trị lớn nhất của hàm số đã cho trên [-1;1] là:
y = 2
y = 1
x = 2
y = 0
Đáp án : A
Quan sát đồ thị và nhận xét.
Hàm số đạt giá trị lớn nhất y = 2.
Cho hàm số f(x) có đồ thị như hình dưới đây:
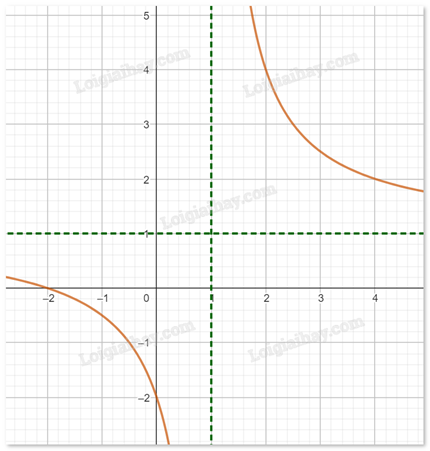
Phát biểu nào sau đây đúng?
Đồ thị hàm số có tiệm cận đứng x = -1, tiệm cận ngang y = 1
Đồ thị hàm số có tiệm cận đứng x = 1, tiệm cận ngang y = -1
Đồ thị hàm số có tiệm cận đứng x = 1, tiệm cận ngang y = 1
Đồ thị hàm số có tiệm cận đứng x = -1, tiệm cận ngang y = -1
Đáp án : C
Quan sát đồ thị và nhận xét.
Quan sát bảng biến thiên thấy đường tiệm cận đứng có hoành độ bằng 1, đường tiệm cận ngang có tung độ bằng 1 nên tiệm cận đứng là x = 1, tiệm cận ngang là y = 1.
Cho hàm số f(x) có đồ thị như hình dưới đây:
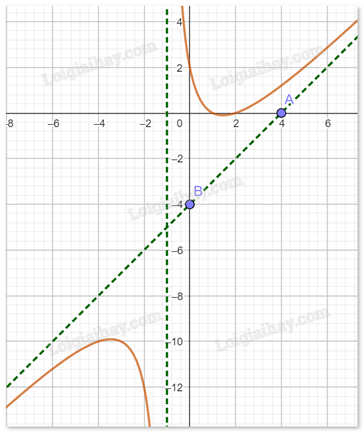
Đường tiệm cận xiên của đồ thị đã cho là đường thẳng:
y = x - 4
y = x + 4
y = 4x
y = 4
Đáp án : A
Tìm 2 điểm mà tiệm cận xiên đi qua, từ đó tìm ra phương trình đường tiệm cận xiên.
Quan sát đồ thị thấy điểm A(4;0) và điểm B(0;-4) thuộc đường tiệm cận xiên, suy ra phương trình đường tiệm cận xiên là y = x – 4.
Cho hàm số f(x) có đồ thị như hình dưới đây:
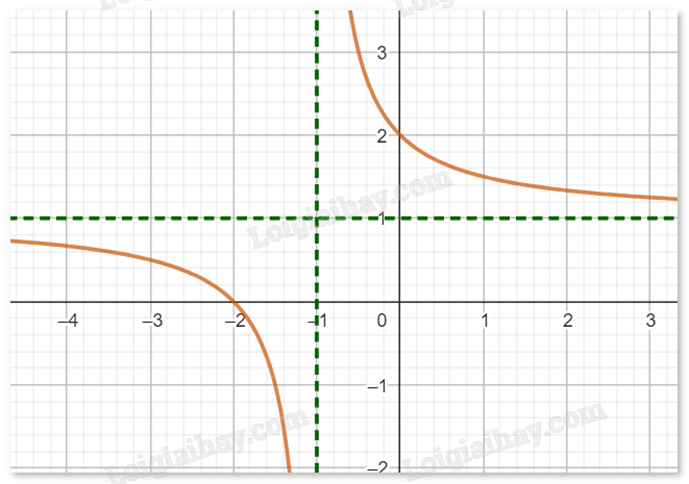
Tâm đối xứng của đồ thị hàm số có tọa độ là:
(1;0)
(0;-1)
(1;1)
(-1;1)
Đáp án : D
Tìm giao điểm hai đường tiệm cận của đồ thị hàm số.
Quan sát đồ thị thấy giao điểm của hai đường tiệm cận có tọa độ (-1;1) suy ra tâm đối xứng của đồ thị hàm số có tọa độ là (-1;1).
Phát biểu nào sau đây là đúng?
Với hai vecto →a,→b bất kì và số thực k, ta có k(→a−→b)=k→a−→b
Với hai vecto →a,→b bất kì và số thực k, ta có k(→a+→b)=k→a−k→b
Với hai vecto →a,→b bất kì và số thực k, ta có k(→a−→b)=k→a→b
Với hai vecto →a,→b bất kì và số thực k, ta có k(→a+→b)=k→a+k→b
Đáp án : D
Dựa vào lí thuyết phép cộng (trừ) và phép nhân vecto với một số.
Theo lý thuyết, ta chọn D.
Hàm số nào sau đây nghịch biến trên R?
y=x−3x+2
y=x3−3x−5
y=−x3−2x−5
y=x2+4
Đáp án : C
Xét tập xác định và y’ của từng hàm số.
Hàm số phải có y′<0 ∀x∈R. Chỉ có đáp án C thỏa mãn vì y′=−3x2−2<0 ∀x∈R.
Giá trị lớn nhất của hàm số (x−2)2.ex trên đoạn [0;3] bằng:
0
4
e
e3
Đáp án : D
Lập bảng biến thiên và tìm GTLN.
y=(x−2)2.ex có tập xác định D=R.
y′=2(x−2).ex+(x−2)2.ex=(x−2).ex.[2+(x−2)]=x.(x−2).ex
y′=0 suy ra x = 0 hoặc x = 2.
Ta có bảng biến thiên:
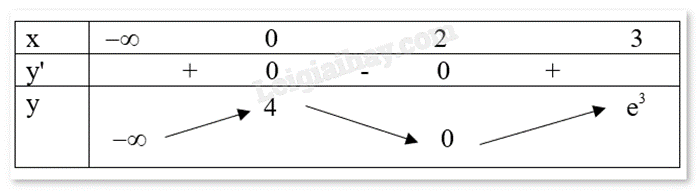
Vậy giá trị lớn nhất của hàm số (x−2)2.ex trên đoạn [0;3] bằng e3.
Quan sát bảng biến thiên và cho biết bảng biến thiên đó là của hàm số nào.
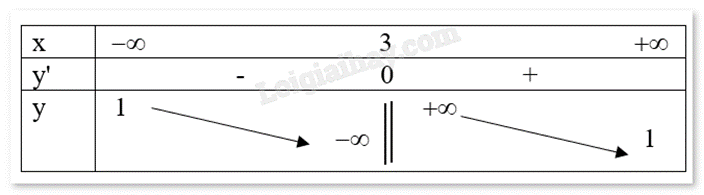
y=x−2x−3
y=x−3x−2
y=x−2x+3
y=3x−2x−1
Đáp án : A
Quan sát bảng biến thiên và nhận xét.
Quan sát bảng biến thiên thấy limx→+∞y=limx→−∞y=1 nên tiệm cận ngang của đồ thị là y = 1, ta loại đáp án D.
Quan sát bảng biến thiên thấy limx→3+y=+∞,limx→3−y=−∞ nên tiệm cận đứng của đồ thị là x = 3, ta loại đáp án B và C.
Đồ thị dưới đây là của hàm số nào?
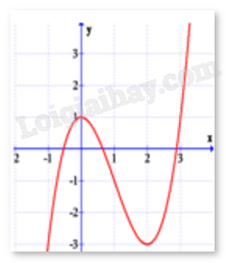
y=−x33+x2+1
y=−x3−3x2+1
y=2x3−6x2+1
y=x3−3x2+1
Đáp án : D
Ta sử dụng cách xác định đồ thị hàm số bậc ba.
Từ hình vẽ tìm một số điểm thuộc đồ thuh hàm số rồi thay tọa độ vào từng đáp án để loại trừ.
Từ hình vẽ ta thấy limx→−∞f(x)=−∞, limx→+∞f(x)=+∞ nên loại A, B.
Đồ thị hàm số đi qua điểm có tọa độ (2;-3) nên thay x = 2; y = -3 vào hai hàm số C, D chỉ thấy hàm số D thỏa mãn.
Cho tứ diện đều ABCD có cạnh bằng 2a. Tích vô hướng →BA.→BC bằng:
a2
2a2
4a2
8a2
Đáp án : B
Áp dụng công thức tính tích vô hướng của hai vecto trong không gian.
cos(→BA.→BC)=→BA.→BC|→BA|.|→BC|⇔cos60o=→BA.→BC2a.2a⇔→BA.→BC=4a2.cos60o=2a2.
Cho hàm số f(x) xác định trên R có bảng biến thiên như sau:

a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
b) Số điểm cực trị của hàm số đã cho là 5
c) Hàm số f(x) có giá trị lớn nhất bằng 3
d) Đồ thị hàm số không có đường tiệm cận
a) Hàm số f(x) đồng biến trên mỗi khoảng (0;2) và (2;3)
b) Số điểm cực trị của hàm số đã cho là 5
c) Hàm số f(x) có giá trị lớn nhất bằng 3
d) Đồ thị hàm số không có đường tiệm cận
Quan sát đồ bảng biến thiên và nhận xét.
a) Sai. Hàm số f(x) nghịch biên trên (0;2) và đồng biến (2;3).
b) Sai. Số điểm cực trị của hàm số đã cho là 3 (x = 0, x = 2, x = 3).
c) Đúng. Hàm số f(x) có giá trị lớn nhất bằng 3.
d) Đúng. Đồ thị hàm số liên tục trên và không có tiệm cận.
Cho hàm số ex−2x+3.
a) Hàm số đã cho nghịch biến trên R
b) Hàm số đã cho đạt cực tiểu tại x = ln2
c) Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0;4)
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ
a) Hàm số đã cho nghịch biến trên R
b) Hàm số đã cho đạt cực tiểu tại x = ln2
c) Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0;4)
d) Đồ thị hàm số đã cho không đi qua gốc tọa độ
Lập bảng biến thiên và nhận xét.
Tập xác định: D=R.
y′=ex−2.
Ta có y′=0⇔ex−2=0⇔x=ln2.
Ta có bảng biến thiên:
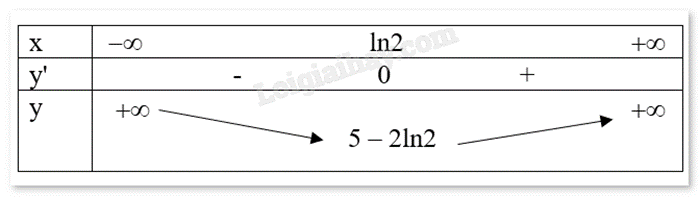
a) Sai. Hàm số f(x) nghịch biên trên (−∞;ln2) và đồng biến trên (ln2;+∞).
b) Đúng. Hàm số đã cho đạt cực tiểu tại x = ln2.
c) Đúng. Vì khi x = 0 thì y = 4, đồ thị đi qua điểm có tọa độ (0;4).
d) Đúng. Vì gốc tọa độ O(0;0) thay vào hàm số thấy không thỏa mãn.
Cho hình hộp ABCD.A’B’C’D’.
a) Các vecto bằng với vecto →AB là →DC,→D′C′,→A′B′
b) Vecto đối của vecto →A′A là →B′B
c) →AB+→DC=2→A′B′
d) →BB′−→CA=→C′A
a) Các vecto bằng với vecto →AB là →DC,→D′C′,→A′B′
b) Vecto đối của vecto →A′A là →B′B
c) →AB+→DC=2→A′B′
d) →BB′−→CA=→C′A
Sử dụng các quy tắc cộng, trừ vecto và lý thuyết các vecto bằng nhau, các vecto đối nhau.
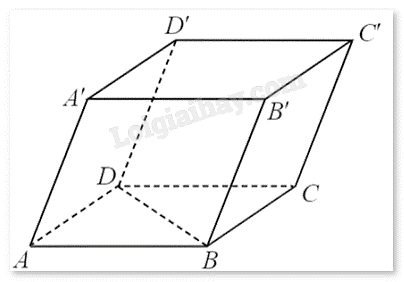
a) Đúng. Các vecto bằng với vecto →AB là →DC,→D′C′,→A′B′ vì chúng cùng phương, cùng chiều và cùng độ dài.
b) Sai. Hai vecto →A′A,→B′B cùng chiều nên không phải vecto đối nhau.
c) Đúng. Vì →AB+→DC=2→AB=2→A′B′.
d) Sai. Vì →BB′−→CA=→CC′−→CA=→AC′.
Cho tứ diện ABCD có BA, BC, BD đôi một vuông góc và BA = BC = BD = 1. Gọi I là trung điểm của AC.
a) →BA+→CD=→BD+→CA
b) →BA.→BD=→BC.→BD=→BC.→BA=−1
c) →BI.→CD=−12
d) (→BI.→CD)=120o
a) →BA+→CD=→BD+→CA
b) →BA.→BD=→BC.→BD=→BC.→BA=−1
c) →BI.→CD=−12
d) (→BI.→CD)=120o
Sử dụng các quy tắc cộng, trừ vecto và lý thuyết các vecto bằng nhau, các vecto đối nhau, góc giữa hai vecto.
a) Đúng. Vì →BA+→CD=→BD+→CA⇔→BA+→AC=→BD+→DC⇔→BC=→BC (luôn đúng)
b) Sai. Vì các vecto →BA,→BC,→BD đôi một vuông góc với nhau nên tích vô hướng của chúng bằng 1.
c) Đúng. Gọi M là trung điểm của AD, ta có IM=BM=BI=DC2 nên tam giác BMI đều.
Suy ra ^MIB=60o=(→IM,→IB)=(→CD,→IB)⇒cos60o=cos(→CD,→IB)
⇒−cos60o=cos(→CD,→BI)⇒cos(→CD,→BI)=−12.
d) Đúng. Vì cos(→CD,→BI)=−12⇒(→CD.→BI)=120o.
Giả sử hàm số x3−3x2+4 đạt cực đại tại x = a và đạt cực tiểu tại x = b. Giá trị của biểu thức a – 2b bằng bao nhiêu?
Đáp án:
Đáp án:
- Tính y’, tìm các nghiệm của y’ = 0
- Lập bảng biến thiên, tìm điểm cực đại, cực tiểu của hàm số
y′=3x2−6x.
y′=0 khi x = 0 hoặc x = 2.
Ta có bảng biến thiên:
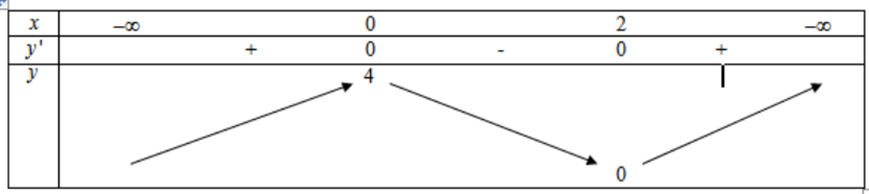
Vậy hàm số đạt cực đại tại x = 0, đạt cực tiểu tại x = 2.
⇒a=0,b=2⇒a−2b=0−2.2=−4.
Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập như hình bên dưới, cho biết M là vị trí của máy bay, OM = 14, ^NOB=32o, ^MOC=65o. Khi đó, tọa độ điểm M có dạng (a;b;c), tính a + b + c (làm tròn đến hàng phần chục).
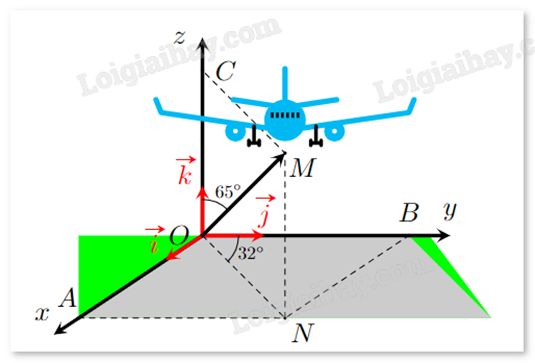
Đáp án:
Đáp án:
Điểm M có hoành độ bằng OA, tung độ bằng OB và cao độ bằng OC.
Sử dụng hệ thức lượng trong tam giác để tính OA, OB, OC.
Ta có:
c=OC=OM.cos65o=14.cos65o.
b=OB=ON.cos32o=OM.sin65o.cos32o=14.sin65o.cos32o.
a=OA=ON.cos(90o−32o)=OMsin65o.cos58o=14.sin65o.cos58o.
Vậy a+b+c≈23,4.
Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của AD và BB’. Cos của góc hợp bởi MN và AC’ bằng √ab với a,b∈N. Tính a+b.
Đáp án:
Đáp án:
Sử dụng phương pháp tọa độ hóa.
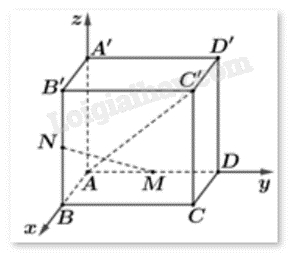
Gọi độ dài cạnh hình lập phương ABCD.A’B’C’D’ là x.
Chọn hệ trục tọa độ Oxyz sao cho O≡A,B∈Ox,D∈Oy,A′∈Oz.
Khi đó, tọa độ các đỉnh là: A(0;0;0),B(a;0;0),D(0;x;0),A′(0;0;x),B′(x;0;x),C(x,x,x).
M là trung điểm của AD suy ra M(0;x2;0).
N là trung điểm của BB’ suy ra N(x;0;x2).
Do đó, →MN=(x;−x2;x2) và →AC′=(x;x;x).
Ta có: cos(MN,AC′)=|cos(→MN,→AC′)|=|→MN.→AC′||→MN|.|→AC′|=x2x√3.x.√62=√23.
⇒a=2,b=3⇒a+b=2+3=5.
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng (gam). Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất?
Đáp án:
Đáp án:
Tìm sản lượng thu hoạch theo số cá trên một đơn vị diện tích, lập bảng biến thiên cho hàm số đó rồi tìm giá trị lớn nhất.
Nếu trên mỗi đơn vị diện tích của mặt hồ có n con cá thì sau một vụ, số cá trên mỗi đơn vị diện tích mặt hồ trung bình nặng f(n)=nP(n)=480n−20n2 (gam).
Xét hàm số f(x)=480x−20x2;x∈(0;+∞).
Ta có: f′(x)=480−40x=0⇔x=12.
Bảng biến thiên:
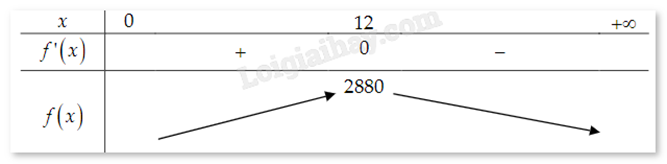
Từ bảng biến thiên, hàm f đạt giá trị lớn nhất tại x = 12. Từ đó, f(n) đạt giá trị lớn nhất tại n = 12.
Cho hàm số y=ax3+bx2+cx+d (a,b,c,d∈R) có đồ thị là đường cong như hình bên. Có bao nhiêu số dương trong các số a,b,c,d?
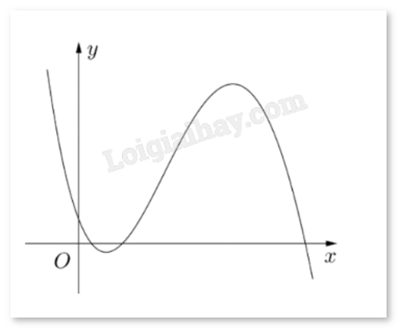
Đáp án:
Đáp án:
Quan sát đồ thị và nhận xét.
Quan sát đồ thị, thấy: limx→+∞y=−∞ suy ra a<0.
Gọi x1,x2 lần lượt là hai điểm cực trị của hàm số đã cho (x1<x2).
Quan sát đồ thị, thấy x1+x2>0 nên ab<0. Mà a < 0 suy ra b > 0.
Quan sát đồ thị, thấy x1.x2>0 nên ac>0. Mà a < 0 suy ra c < 0.
Đồ thị hàm số giao trục tung tại điểm có tung độ d nằm phía trên trục hoành suy ra d>0.
Vậy, trong các số a,b,c,d có hai số b,d dương.
Tìm hai số có hiệu là 13 sao cho tích của chúng bé nhất. Tổng hai số đó bằng bao nhiêu?
Đáp án:
Đáp án:
Ứng dụng đạo hàm và sử dụng bảng biến thiên.
Gọi một trong hai số phải tim là x, số kia là x + 13.
Xét tích P(x)=x(13+x).
Ta có P′(x)=2x+13=0⇔x=−132.
Bảng biến thiên:
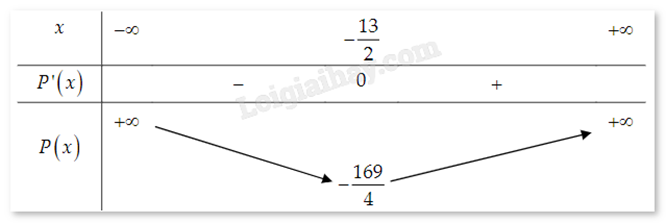
Từ bảng biến thiên, ta có minP(x)=P(−132)=−1694. Vậy tích hai số bé nhất khi một số là −132 và số kia là 132. Tổng của chúng bằng 0.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365