Bài 1 (3 điểm):

Tính:

a) $A = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 9x + 14}}{{x - 2}}$

b) $B = \mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt[3]{{8{x^3} + 1}} - x} \right)$

c) $C = \mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} \frac{{\left| {{x^2} + 7x + 12} \right|}}{{x + 3}}$

Bài 2 (1 điểm):

Định $a$ để hàm số sau đây liên tục tại ${x_0} =  - 4$: $f\left( x \right) = \left\{ \begin{array}{l}\frac{{x + 4}}{{\sqrt {x + 13}  - 3}}\,\,\,\left( {x >  - 4} \right)\\{x^2} + 2a\,\,\,\,\,\,\,\,\,\,\,\,\left( {x \le  - 4} \right)\end{array} \right.$

Bài 3 (1 điểm):

Tìm đạo hàm của hàm số $y = f\left( x \right) = \sqrt {\frac{1}{x} + \tan x}$.

Bài 4 (1 điểm):

Cho hàm số $y = f\left( x \right) = \frac{{2x + 5}}{{x - 3}}$ có đồ thị $\left( C \right)$. Viết phương trình tiếp tuyến $\left( \Delta  \right)$ của đồ thị $\left( C \right)$ biết $\left( \Delta  \right)$ song song với đường thẳng $\left( D \right):y =  - 11x$.

Bài 5 (4 điểm):

Cho hình chóp $S.ABC$ có $\Delta ABC$ vuông cân tại $C$, $CA = a,SC \bot \left( {ABC} \right)$.

a) Chứng minh $AC \bot \left( {SBC} \right)$.

b) Gọi $I$ là trung điểm của $AB$. Chứng minh $\left( {SCI} \right) \bot \left( {SAB} \right)$.

c) Cho $SC = \frac{{a\sqrt 6 }}{2}$. Tính $\widehat {\left( {\left( {SAB} \right),\left( {ABC} \right)} \right)}$.

d) Gọi $H$ là điểm thuộc đoạn $CI$ sao cho $CH = 3HI$. Trên đường thẳng đi qua $H$ và vuông góc với mặt phẳng $\left( {ABC} \right)$, lấy điểm $D$ sao cho $DH = \frac{{a\sqrt {14} }}{8}$. Gọi ${G_1}$ và ${G_2}$ lần lượt là trọng tâm của các tam giác $DAC$ và $DBC$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $\left( {C{G_1}{G_2}} \right)$.

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn baitap365.com

Bài 1 (VD):

Phương pháp:

a) Khử dạng vô định bằng cách phân tích tử thành nhân tử.

b) Đặt $x$ ra ngoài và sử dụng qui tắc tính giới hạn

c) Khử dạng vô định bằng cách phân tích tử thành nhân tử.

Cách giải:

Tính:

a) $A = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 9x + 14}}{{x - 2}}$

$\begin{array}{l} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x - 2} \right)\left( {x - 7} \right)}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \left( {x - 7} \right)\\ = 2 - 7\\ =  - 5\end{array}$

b) $B = \mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt[3]{{8{x^3} + 1}} - x} \right)$

$\begin{array}{l} = \mathop {\lim }\limits_{x \to  + \infty } \left( {x\sqrt[3]{{2 + \frac{1}{{{x^3}}}}} - x} \right)\\ = \mathop {\lim }\limits_{x \to  + \infty } \left[ {x.\left( {\sqrt[3]{{2 + \frac{1}{{{x^3}}}}} - 1} \right)} \right]\\ =  + \infty \end{array}$

Vì $\mathop {\lim }\limits_{x \to  + \infty } x =  + \infty$ và $= \mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt[3]{{2 + \frac{1}{{{x^3}}}}} - 1} \right)$ $= \sqrt[3]{2} - 1 > 0$.

c) $C = \mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} \frac{{\left| {{x^2} + 7x + 12} \right|}}{{x + 3}}$

$\begin{array}{l} = \mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} \frac{{\left| {\left( {x + 3} \right)\left( {x + 4} \right)} \right|}}{{x + 3}}\\ = \mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} \frac{{ - \left( {x + 3} \right)\left| {x + 4} \right|}}{{x + 3}}\\ = \mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} \left( { - \left| {x + 4} \right|} \right)\\ =  - \left( { - 3 + 4} \right) =  - 1\end{array}$

Bài 2 (VD):

Phương pháp:

Tính $\mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ + }} f\left( x \right);\mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ - }} f\left( x \right);f\left( { - 4} \right)$

Để hàm số liên tục tại ${x_0} =  - 4$ thì $\mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ - }} f\left( x \right)$ $= f\left( { - 4} \right)$

Cách giải:

 Định $a$ để hàm số sau đây liên tục tại ${x_0} =  - 4$:

$f\left( x \right) = \left\{ \begin{array}{l}\frac{{x + 4}}{{\sqrt {x + 13}  - 3}}\,\,\,\left( {x >  - 4} \right)\\{x^2} + 2a\,\,\,\,\,\,\,\,\,\,\,\,\left( {x \le  - 4} \right)\end{array} \right.$

Ta có: $\mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ + }} f\left( x \right)$

$\begin{array}{l} = \mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ + }} \frac{{x + 4}}{{\sqrt {x + 13}  - 3}}\\ = \mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ + }} \frac{{\left( {x + 4} \right)\left( {\sqrt {x + 13}  + 3} \right)}}{{x + 13 - 9}}\end{array}$

$\begin{array}{l} = \mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ + }} \frac{{\left( {x + 4} \right)\left( {\sqrt {x + 13}  + 3} \right)}}{{x + 4}}\\ = \mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ + }} \left( {\sqrt {x + 13}  + 3} \right)\\ = \sqrt {\left( { - 4} \right) + 13}  + 3 = 6\end{array}$

$\begin{array}{l}\mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ - }} f\left( x \right)\\ = \mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ - }} \left( {{x^2} + 2a} \right)\\ = {\left( { - 4} \right)^2} + 2a = 2a + 16\end{array}$

$f\left( { - 4} \right) = {\left( { - 4} \right)^2} + 2a$ $= 2a + 16$

Để hàm số đã cho liên tục tại ${x_0} =  - 4$ thì $\mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { - 4} \right)}^ - }} f\left( x \right)$ $= f\left( { - 4} \right)$

$\begin{array}{l} \Leftrightarrow 2a + 16 = 6\\ \Leftrightarrow 2a =  - 10\\ \Leftrightarrow a =  - 5\end{array}$

Vậy $a =  - 5$ là giá trị cần tìm.

Bài 3 (VD):

Phương pháp:

Sử dụng công thức tính đạo hàm $\left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}$, ${\left( {\frac{1}{x}} \right)'} =  - \frac{1}{{{x^2}}};\left( {\tan x} \right)' = \frac{1}{{{{\cos }^2}x}}$

Cách giải:

Ta có:

$\begin{array}{l}y' = {\left( {\sqrt {\frac{1}{x} + \tan x} } \right)'}\\ = \frac{{{{\left( {\frac{1}{x} + \tan x} \right)}'}}}{{2\sqrt {\frac{1}{x} + \tan x} }}\\ = \frac{{\frac{{ - 1}}{{{x^2}}} + \frac{1}{{{{\cos }^2}x}}}}{{2\sqrt {\frac{1}{x} + \tan x} }}\\ = \frac{{{x^2} - {{\cos }^2}x}}{{2{x^2}{{\cos }^2}x.\sqrt {\frac{1}{x} + \tan x} }}\end{array}$

Bài 4 (VD):

Phương pháp:

Phương trình tiếp tuyến với đồ thị hàm số $y = f\left( x \right)$ tại điểm ${M_0}\left( {{x_0};{y_0}} \right)$ là:

$y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}$

Hai đường thẳng song song thì có cùng hệ số góc.

Cách giải:

TXĐ: $D = \mathbb{R}\backslash \left\{ 3 \right\}$

Ta có: $y' = \frac{{ - 11}}{{{{\left( {x - 3} \right)}^2}}}$

Gọi $M\left( {{x_0};{y_0}} \right)$ là tọa độ tiếp điểm của tiếp tuyến $\left( \Delta  \right)$ với đồ thị hàm số

Vì $\left( \Delta  \right)//\left( D \right)$ nên hệ số góc của $\left( \Delta  \right)$ là $f'\left( {{x_0}} \right) =  - 11$

$\Leftrightarrow \frac{{ - 11}}{{{{\left( {x - 3} \right)}^2}}} =  - 11$

$\begin{array}{l} \Leftrightarrow {\left( {{x_0} - 3} \right)^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} - 3 = 1\\{x_0} - 3 =  - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 4 \Rightarrow {y_0} = 13\\{x_0} = 2 \Rightarrow {y_0} =  - 9\end{array} \right.\end{array}$

Với $M\left( {4;13} \right)$ ta có phương trình tiếp tuyến $\left( \Delta  \right):$ $y =  - 11\left( {x - 4} \right) + 13$ $\Leftrightarrow y =  - 11x + 57$

Với $M\left( {2; - 9} \right)$ ta có phương trình tiếp tuyến $\left( \Delta  \right):$ $y =  - 11\left( {x - 2} \right) - 9$ $\Leftrightarrow y =  - 11x + 13$

Vậy có hai tiếp tuyến thỏa mãn đề bài: $y =  - 11x + 57$, $y =  - 11x + 13$.

Bài 5 (VD):

Phương pháp:

a) Thay $x = 3$ vào hàm số dưới dấu giới hạn.

b) Khử dạng vô định bằng cách phân tích tử thành nhân tử.

c) Chia cả tử và mẫu cho $n$ và áp dụng quy tắc tính giới hạn.

Cách giải:

Cho hình chóp $S.ABC$ có $\Delta ABC$ vuông cân tại $C$, $CA = a,SC \bot \left( {ABC} \right)$.

a) Chứng minh $AC \bot \left( {SBC} \right)$.

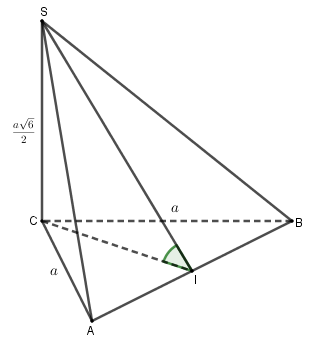
$\Delta ABC$ vuông tại $C$ nên $AC \bot BC$.

$SC \bot \left( {ABC} \right)$, mà $AC \subset \left( {ABC} \right)$ nên $SC \bot AC$.

Ta có: $\left\{ \begin{array}{l}AC \bot CB\\AC \bot SC\end{array} \right.$ $\Rightarrow AC \bot \left( {SBC} \right)$ (đpcm).

b) Gọi $I$ là trung điểm của $AB$. Chứng minh $\left( {SCI} \right) \bot \left( {SAB} \right)$.

Tam giác $ABC$ vuông cân tại $C$ nên $CI$ vừa là đường trung tuyến, vừa là đường cao

$\Rightarrow CI \bot AB$.

$SC \bot \left( {ABC} \right)$, mà $AB \subset \left( {ABC} \right)$ nên $SC \bot AB$.

Ta có: $\left\{ \begin{array}{l}AB \bot CI\\AB \bot SC\end{array} \right. \Rightarrow AB \bot \left( {SCI} \right)$

Mà $AB \subset \left( {SAB} \right)$ nên $\left( {SAB} \right) \bot \left( {SCI} \right)$ (đpcm).

c) Cho $SC = \frac{{a\sqrt 6 }}{2}$. Tính $\widehat {\left( {\left( {SAB} \right),\left( {ABC} \right)} \right)}$.

Theo câu b, $AB \bot \left( {SCI} \right) \Rightarrow AB \bot SI$

Ta có:

$\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\SI \bot AB,SI \subset \left( {SAB} \right)\\CI \bot AB,CI \subset \left( {ABC} \right)\end{array} \right.$ $\Rightarrow \widehat {\left( {\left( {SAB} \right),\left( {ABC} \right)} \right)} = \widehat {\left( {SI,CI} \right)}$ $= \widehat {SIC}$ (vì $\widehat {SIC} < \widehat {SCI} = {90^0}$)

Tam giác $ABC$ vuông cân tại $C$ có $CA = CB = a$ nên theo pitago ta có:

$AB = \sqrt {C{A^2} + C{B^2}}$ $= \sqrt {{a^2} + {a^2}}  = a\sqrt 2$

$\Rightarrow CI = IA = \frac{1}{2}AB = \frac{{a\sqrt 2 }}{2}$

Tam giác $SCI$ vuông tại $C$ có $\tan \widehat {SIC} = \frac{{SC}}{{CI}}$ $= \frac{{a\sqrt 6 }}{2}:\frac{{a\sqrt 2 }}{2} = \sqrt 3$

$\Rightarrow \widehat {SIC} = {60^0}$.

Vậy góc giữa $\left( {SAB} \right)$ và $\left( {ABC} \right)$ bằng ${60^0}$.

d) Gọi $H$ là điểm thuộc đoạn $CI$ sao cho $CH = 3HI$. Trên đường thẳng đi qua $H$ và vuông góc với mặt phẳng $\left( {ABC} \right)$, lấy điểm $D$ sao cho $DH = \frac{{a\sqrt {14} }}{8}$. Gọi ${G_1}$ và ${G_2}$ lần lượt là trọng tâm của các tam giác $DAC$ và $DBC$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $\left( {C{G_1}{G_2}} \right)$.

Gọi $E,F$ lần lượt là trung điểm của $DA,DB$.

Do ${G_1},{G_2}$ lần lượt là trọng tâm của các tam giác $DAC$ và $DBC$ nên:

$\left\{ \begin{array}{l}\frac{{C{G_1}}}{{CE}} = \frac{2}{3}\\\frac{{C{G_2}}}{{CF}} = \frac{2}{3}\end{array} \right.$ $\Rightarrow \frac{{C{G_1}}}{{CE}} = \frac{{C{G_2}}}{{CF}}$ $\Rightarrow {G_1}{G_2}//EF$

Mà $EF//AB$ (do $EF$ là đường trung bình của tam giác $DAB$)

Nên $AB//\left( {C{G_1}{G_2}} \right) \equiv \left( {CEF} \right)$

$\Rightarrow d\left( {A,\left( {C{G_1}{G_2}} \right)} \right) = d\left( {I,\left( {CEF} \right)} \right)$.

Gọi $K = DI \cap EF$, ta chứng minh $IK \bot \left( {CEF} \right)$.

Ta có: $DH \bot \left( {ABC} \right),SC \bot \left( {ABC} \right)$ $\Rightarrow DH//SC$

$\Rightarrow$ các điểm $D,H,S,C,I$ đồng phẳng hay $DH \subset \left( {SCI} \right)$.

Ta có: $AB \bot \left( {SCI} \right)$ và $AB//\left( {CEF} \right)$

$\Rightarrow \left( {CEF} \right) \bot \left( {DCI} \right)$.

Tam giác $DCH$ vuông tại $H$ có: $DH = \frac{{a\sqrt {14} }}{8},$ $CH = \frac{3}{4}CI = \frac{{a\sqrt 3 }}{8}$ nên theo Pitago ta có:

$CD = \sqrt {D{H^2} + A{H^2}}$ $= \sqrt {{{\left( {\frac{{a\sqrt {14} }}{8}} \right)}^2} + {{\left( {\frac{{3a\sqrt 2 }}{8}} \right)}^2}}  = \frac{{a\sqrt 2 }}{2}$

$\Rightarrow CD = CI = \frac{{a\sqrt 2 }}{2}$ $\Rightarrow \Delta CDI$ cân tại $C$.

Lại có $K$ là trung điểm $DI$ (do $K$ nằm trên $EF$ là đường trung bình của $\Delta DAB$)

Nên $CK \bot DI \Rightarrow CK \bot IK$.

Ta có:

$\left\{ \begin{array}{l}\left( {CEF} \right) \bot \left( {DCI} \right)\\\left( {CEF} \right) \cap \left( {DCI} \right) = CK\\IK \subset \left( {DCI} \right)\\IK \bot CK\end{array} \right.$ $\Rightarrow IK \bot \left( {CEF} \right)$ $\Rightarrow d\left( {I,\left( {CEF} \right)} \right) = IK$

Xét tam giác $DHI$ vuông tại $H$ có: $DH = \frac{{a\sqrt {14} }}{8},$ $HI = \frac{1}{4}CI = \frac{{a\sqrt 2 }}{8}$ nên theo Pitago ta có:

$DI = \sqrt {D{H^2} + H{I^2}}$ $= \sqrt {{{\left( {\frac{{a\sqrt {14} }}{8}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{8}} \right)}^2}}  = \frac{a}{2}$

$\Rightarrow IK = \frac{1}{2}DI = \frac{1}{2}.\frac{a}{2} = \frac{a}{4}$.

Vậy $d\left( {A,\left( {C{G_1}{G_2}} \right)} \right) = \frac{a}{4}$.

HẾT

baitap365.com