Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Bài 2. Giới hạn của hàm số Toán 11 Chân trời sáng tạo
Giải mục 3 trang 73, 74, 75 SGK Toán 11 tập 1 - Chân trời sáng tạo
Giải mục 4 trang 75, 76 SGK Toán 11 tập 1 - Chân trời sáng tạo Giải mục 5 trang 77, 78 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 1 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 2 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 3 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 4 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 5 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo Bài 6 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo Giải mục 2 trang 72, 73 SGK Toán 11 tập 1 - Chân trời sáng tạo Giải mục 1 trang 71, 72 SGK Toán 11 tập 1 - Chân trời sáng tạo Lý thuyết Giới hạn của hàm số - SGK Toán 11 Chân trời sáng tạoGiải mục 3 trang 73, 74, 75 SGK Toán 11 tập 1 - Chân trời sáng tạo
Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị cung cấp được cho bởi bảng sau:
Hoạt động 3
Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị cung cấp được cho bởi bảng sau:

Nếu chỉ xét trên khoảng từ 0 đến 5 (tính theo 100 gam) thì hàm số giả cước (tính theo nghìn đồng) xác định như sau:
f(x)={6khix∈(0;1]7khix∈(1;2,5]10khix∈(2,5;5]
Đồ thị của hàm số như Hình 2.
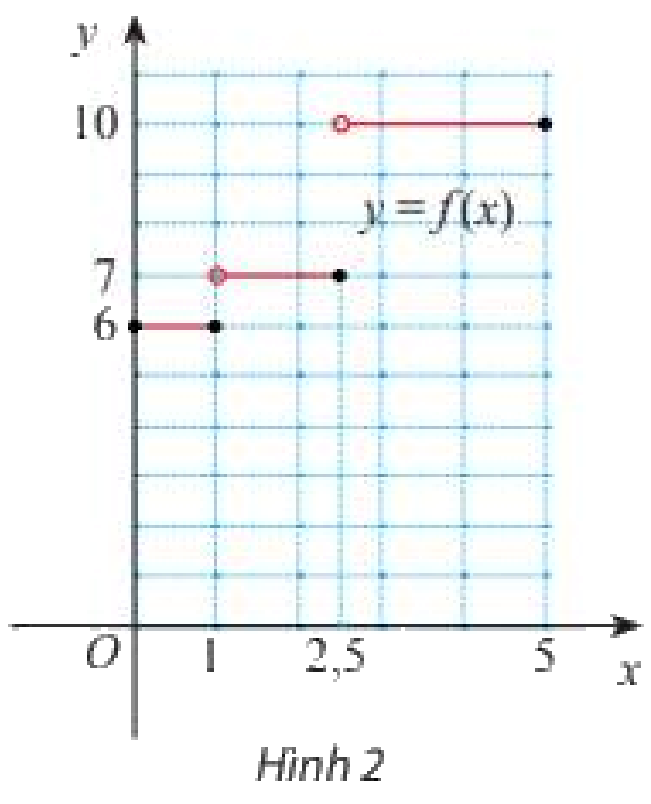
a) Giả sử (xn) là dãy số bất kì sao cho x∈(1;2,5) và limxn=1. Tìm limf(xn).
b) Giả sử (xn′) là dãy số bất kì sao cho xn′∈(0;1) và limxn′=1. Tìm limf(xn′).
c) Nhận xét về kết quả ở a) và b)
Thực hành 3
Cho hàm số f(x)={1−2xkhix≤−1x2+2khix>−1.
Tìm các giới hạn limx→−1+f(x),limx→−1−f(x) và limx→−1f(x) (nếu có).
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365