Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 7 Kết nối tri thức
Đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 6
Đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 7 Đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 8 Đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 9 Đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 10 Đề thi giữa kì 2 Toán 7 - Đề số 5 - Kết nối tri thức Đề thi giữa kì 2 Toán 7 - Đề số 4 - Kết nối tri thức Đề thi giữa kì 2 Toán 7 - Đề số 3 - Kết nối tri thức Đề thi giữa kì 2 Toán 7 - Đề số 2 - Kết nối tri thức Đề thi giữa kì 2 Toán 7 - Đề số 1 - Kết nối tri thứcĐề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 6
Phần trắc nghiệm (3 điểm) Câu 1: Trong các cặp tỉ số sau, cặp tỉ số nào lập thành một tỉ lệ thức?
Trong các cặp tỉ số sau, cặp tỉ số nào lập thành một tỉ lệ thức?
Đáp án : A
Tỉ lệ thức là đẳng thức của hai tỉ số ab=cdab=cd.
Ta có: 12:18=1218=2312:18=1218=23 nên cặp tỉ số A lập thành một tỉ lệ thức.
12:18=1218=23≠3212:18=1218=23≠32 nên cặp tỉ số B không lập thành một tỉ lệ thức.
12−18=−23≠2312−18=−23≠23 nên cặp tỉ số C không lập thành một tỉ lệ thức.
(−12):(−18)=−12−18=23≠−23(−12):(−18)=−12−18=23≠−23 nên cặp tỉ số D không lập thành một tỉ lệ thức.
Cho tỉ lệ thức ab=cd.ab=cd. Khẳng định đúng là
Đáp án : B
Dựa vào tính chất cơ bản của tỉ lệ thức.
Áp dụng tính chất cơ bản của tỉ lệ thức, ta có:
Nếu ab=cdab=cd thì ad=bcad=bc.
Từ đẳng thức 2.(−15)=(−5).62.(−15)=(−5).6, ta có thể lập được tỉ lệ thức nào?
Đáp án : D
Ta sử dụng tính chất: Nếu ad=bcad=bc thì ab=cd;ac=bd;db=ca;dc=baab=cd;ac=bd;db=ca;dc=ba.
Từ đẳng thức 2.(−15)=(−5).62.(−15)=(−5).6, ta có:
2−5=6−15;26=−5−15;−52=−156;62=−15−52−5=6−15;26=−5−15;−52=−156;62=−15−5.
⇒⇒ Đáp án D là đáp án đúng.
Cho x,yx,y là hai đại lượng tỉ lệ nghịch với nhau, biết x1,y1x1,y1 và x2,y2x2,y2 là các cặp giá trị tương ứng của chúng. Khẳng định nào sau đây là sai?
x1y2=x2y1.x1y2=x2y1.
y1x1=x2y2.y1x1=x2y2.
Đáp án : B
Dựa vào tính chất của hai đại lượng tỉ lệ nghịch.
x, y là hai đại lượng tỉ lệ nghịch với nhau nên x1x2=y2y1x1x2=y2y1; x1y2=x2y1x1y2=x2y1; x1y1=x2y2
⇒A,C,D đúng.
Nếu ba số a;b;c tương ứng tỉ lệ với 2;5;7 ta có dãy tỉ số bằng nhau là:
Đáp án : D
Dựa vào kiến thức về dãy tỉ số bằng nhau.
Vì a; b; c tương ứng tỉ lệ với 2; 5; 7 nên ta có dãy tỉ số bằng nhau là:
a2=b5=c7.
Cho đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k=−3. Hệ thức liên hệ của y và x là:
Đáp án : B
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k=−3 ta có hệ thức liên hệ của y và x là y=−3x.
Biểu thức nào là đa thức một biến?
Đáp án : B
Dựa vào kiến thức về đa thức một biến.
Trong các biểu thức trên, 2x3−x2+5 là đa thức một biến.
Trong hình vẽ bên, có điểm C nằm giữa B và D. So sánh AB;AC;AD ta được
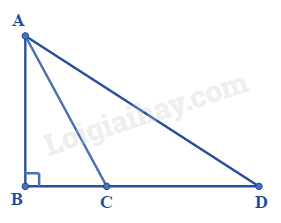
Đáp án : B
Dựa vào quan hệ giữa đường xiên và hình chiếu.
Vì AB < BD, C nằm giữa B và D nên BC < BD.
Do đó AB < AC < AD. (quan hệ giữa đường xiên và hình chiếu).
Trong các bộ ba đoạn thẳng sau đây. Bộ gồm ba đoạn thẳng nào là độ dài ba cạnh của một tam giác?
Đáp án : C
Dựa vào quan hệ giữa ba cạnh của một tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại.
Ta có: 5=3+2 nên 5cm,3cm,2cm không là độ dài ba cạnh của một tam giác.
1+1=2<5 nên 5cm,1cm,1cm không là độ dài ba cạnh của một tam giác.
5+3=8>6;5+6=11>3;3+6=9>5 nên 5cm,3cm,6cm là độ dài ba cạnh của một tam giác.
5+5=10 nên 5cm,5cm,10cm không là độ dài ba cạnh của một tam giác.
Cho đại lượng y tỉ lệ thuận với đại lượng x. Khi x=4 thì y=16 . Vậy hệ số tỉ lệ bằng
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Đại lượng y tỉ lệ thuận với đại lượng x nên hệ số tỉ lệ là:
k=yx=164=4.
Biểu thức biểu thị chu vi của hình chữ nhật có chiều dài 8cm và chiều rộng 6cm là
Đáp án : D
Dựa vào kiến thức về biểu thức số, công thức tính chu vi của hình chữ nhật.
Biểu thức biểu thị chu vi của hình chữ nhật là:
(6+8).2(cm).
Đường vuông góc kẻ từ H xuống đường thẳng m là:
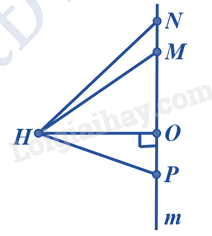
Đáp án : C
Dựa vào kiến thức về đường vuông góc.
Đường vuông góc kẻ từ H xuống đường thẳng m là HO.
a) Tìm x biết 6x=−45.
b) Tìm x;y biết: x5=y3 và x+2y=33.
c) Tìm a, b, c tỉ lệ với ba số 2; 3; -4 và a + b – c = 18.
a) Dựa vào tính chất của tỉ lệ thức để tìm x.
b, c) Sử dụng tính chất của dãy tỉ số bằng nhau để tìm ẩn.
a) Ta có:
6x=−456.5=−4.x−4x=30x=−304=−152
Vậy x=−152.
b) Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
x5=y3=x+2y5+2.3=3311=3
Từ đó suy ra:
x=3.5=15y=3.3=9
Vậy x = 15; y = 9.
c) Ta có a, b, c tỉ lệ với ba số 2; 3; -4 nên ta có dãy tỉ số bằng nhau:
a2=b3=c−4
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
a2=b3=c−4=a+b−c2+3−(−4)=189=2
Từ đó suy ra:
a=2.2=4b=2.3=6c=2.(−4)=−8
Vậy a=4;b=6;c=−8.
Số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 21; 20; 22. Tính số học sinh của mỗi lớp, biết rằng lớp 7C có nhiều hơn lớp 7A là 2 học sinh.
Áp dụng tính chất của dãy tỉ số bằng nhau để tìm số học sinh của mỗi lớp.
Gọi số học sinh lớp 7A, 7B, 7C lần lượt là a, b, c (a,b,c∈N∗,c>2) (học sinh)
Vì số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 21; 20; 22 nên ta có dãy tỉ số bằng nhau:
a21=b20=c22
Do lớp 7C có nhiều hơn lớp 7A 2 học sinh nên áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
b20=c22=a21=c−a22−21=21=2.
Từ đó suy ra:
c=2.22=44a=2.21=42b=2.20=40 (Thỏa mãn)
Vậy số học sinh lớp 7A, 7B, 7C lần lượt là 42; 40; 44 học sinh.
Một khu đất hình chữ nhật có chiều dài và chiều rộng tỉ lệ với 8 và 5. Diện tích khu đất đó bằng 360m2. Tính chiều dài và chiều rộng của khu đất đó.
Áp dụng tính chất của dãy tỉ số bằng nhau và công thức tính diện tích hình chữ nhật để tìm chiều dài và chiều rộng của khu đất đó.
Gọi chiều dài và chiều rộng của khu đất lần lượt là x,y(x>y>0) (m).
Vì chiều dài và chiều rộng tỉ lệ với 8 và 5 nên ta có:
x8=y5=k(k>0) suy ra x=8k;y=5k.
Mà diện tích khu đất bằng 360m2 nên ta có x.y=360 hay 8k.5k=360
40k2=360k2=9
k=3 (vì k>0)
Từ đó suy ra:
x=8.3=24y=5.3=15(thỏa mãn)
Vậy chiều dài và chiều rộng của khu đất đó lần lượt là 24m và 15m.
Cho tam giác ABC cân tại A. Từ A kẻ AH vuông góc với BC tại H, trên đoạn thẳng AH lấy điểm M tùy ý (M khác A và H). Chứng minh rằng:
a) BH = CH.
b) BA > BM.
a) Chứng minh ΔAHB=ΔAHC nên BH=CH.
b) Sử dụng quan hệ giữa đường vuông góc và đường xiên để chứng minh.
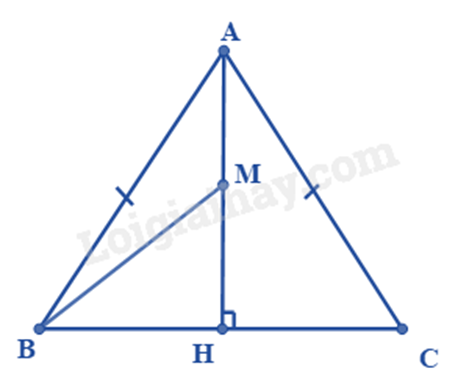
a) Xét ΔAHB và ΔAHC có:
^AHB=^AHC=900
AB=AC (ΔABC cân tại A)
AH chung
Suy ra ΔAHB=ΔAHC (cạnh huyền – cạnh góc vuông)
Suy ra BH=CH (hai cạnh tương ứng) (đpcm)
b) Do M nằm giữa A và H nên HA > HM.
Ta có BH là đường vuông góc, BA và BM là các đường xiên kẻ từ B đến đường thẳng AH nên HM là hình chiếu của BM, HA là hình chiếu của AB xuống AH.
Vì HA > HM nên BA < BM.
Vậy BA > BM (đpcm).
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng AB+AC>2AM.
Dựa vào kiến thức về đường trung tuyến trong tam giác.
Lấy điểm D thuộc tia đối của tia AM sao cho AM = DM.
Chứng minh ΔAMB=ΔDMC suy ra AB=CD.
Sử dụng bất đẳng thức tam giác để chứng minh AB+AC>AD=2AM.
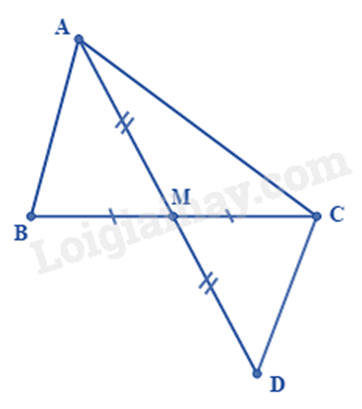
Do AM là trung tuyến của tam giác ABC nên ta có BM = CM.
Trên tia đối của tia AM lấy điểm D sao cho AM = DM.
Xét ΔAMB và ΔDMC có:
AM=DM
BM=CM
^AMB=^DMC (hai góc đối đỉnh)
Suy ra ΔAMB=ΔDMC (c.g.c) suy ra AB = CD (hai cạnh tương ứng)
Khi đó AB+AC=DC+AC>AD (bất đẳng thức tam giác)
Mà AM = DM nên AD = 2.AM
Do đó: AB+AC>2AM.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365