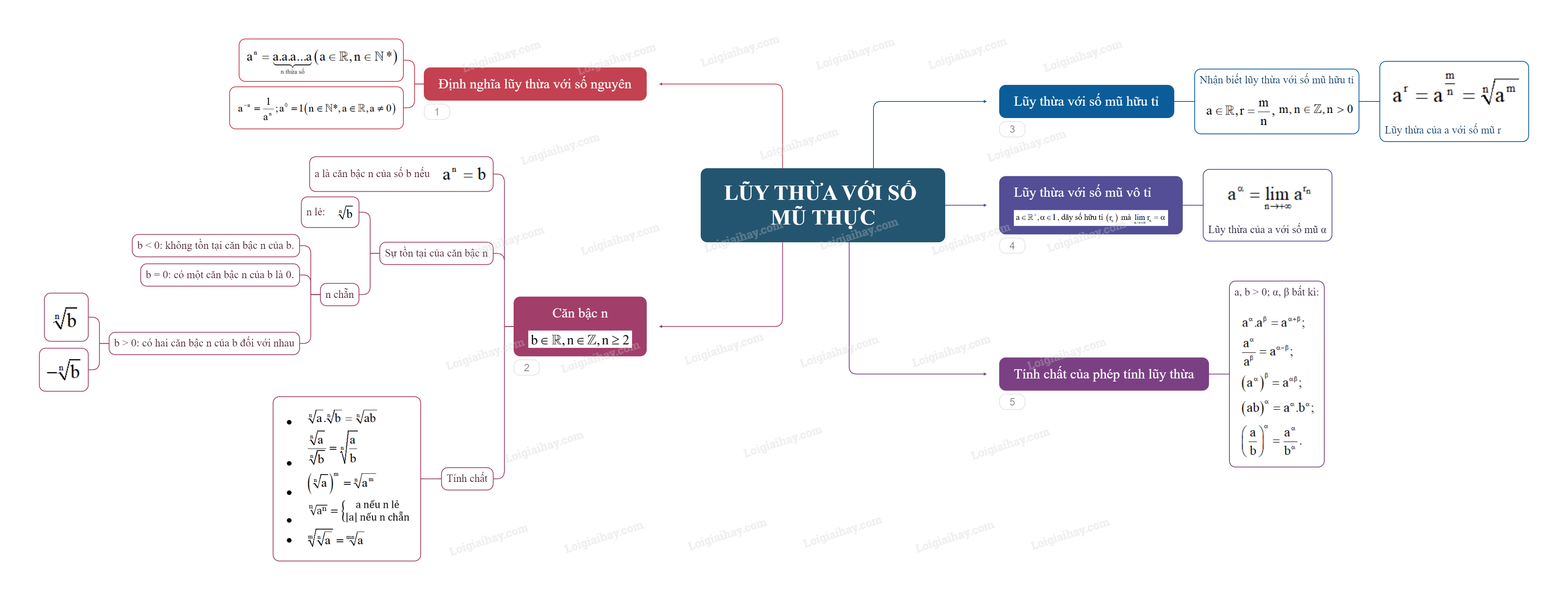
1. Lũy thừa với số mũ nguyên

- Lũy thừa với số mũ nguyên dương:

${a^n} = \underbrace {a.a.a...a}_{n\,thừa\,số}\left( {a \in \mathbb{R},n \in \mathbb{N}*} \right)$.

- Lũy thừa với số mũ nguyên âm, số mũ 0:

${a^{ - n}} = \frac{1}{{{a^n}}};{a^0} = 1\left( {n \in \mathbb{N}*,a \in \mathbb{R},a \ne 0} \right)$.

2. Căn bậc n

Cho số thực b và số nguyên $n \ge 2$.

- Số a là căn bậc n của số b nếu ${a^n} = b$.

- Sự tồn tại căn bậc n:

+ Nếu n lẻ thì có duy nhất một căn bậc n của b, kí hiệu $\sqrt[n]{b}$.

+ Nếu n chẵn thì:

• b < 0: không tồn tại căn bậc n của b.
• b = 0: có một căn bậc n của b là 0.
• b > 0: có hai căn bậc n của b đối với nhau, kí hiệu giá trị dương là $\sqrt[n]{b}$ và giá trị âm là $- \sqrt[n]{b}$.

+ Các tính chất:

• $\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}$
• $\frac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}} = \sqrt[n]{{\frac{a}{b}}}$
• ${\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}}$
• $\sqrt[m]{{\sqrt[n]{a}}} = \sqrt[{mn}]{a}$

3. Lũy thừa với số mũ hữu tỉ

Cho số thực dương a và số hữu tỉ $r = \frac{m}{n}$, trong đó $m,n \in \mathbb{Z},n > 0$. Ta có:

${a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}$

4. Lũy thừa với số mũ vô tỉ

Giả sử a là một số dương, $\alpha$ là một số vô tỉ và $\left( {{r_n}} \right)$ là một dãy số hữu tỉ sao cho $\lim {r_n} = \alpha$. Khi đó ${a^\alpha } = \mathop {\lim }\limits_{n \to  + \infty }  = {a^{{r_n}}}$.

5. Tính chất của phép tính lũy thừa

Cho a, b là những số thực dương; $\alpha ;\beta$ là những số thực bất kì. Khi đó:

$\begin{array}{l}{a^\alpha }.{a^\beta } = {a^{\alpha  + \beta }};\\\frac{{{a^\alpha }}}{{{a^\beta }}} = {a^{\alpha  - \beta }};\\{\left( {{a^\alpha }} \right)^\beta } = {a^{\alpha \beta }};\\{\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha };\\{\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}.\end{array}$