Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 8 - Kết nối tri thức
Đề thi giữa kì 2 Toán 8 - Đề số 6 - Kết nối tri thức
Đề thi giữa kì 2 Toán 8 - Đề số 7 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 8 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 5 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 4 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 3 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 2 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 1 - Kết nối tri thứcĐề thi giữa kì 2 Toán 8 - Đề số 6 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Câu 1: Biểu thức nào dưới đây là phân thức đại số?
Biểu thức nào dưới đây là phân thức đại số?
Đáp án : B
Sử dụng khái niệm về phân thức đại số.
Nhớ lại định nghĩa về đa thức, đơn thức.
x+y√7z không là phân thức vì mẫu số không là đa thức
x3−3x2+2xz−y là phân thức vì cả tử và mẫu số là đa thức với mẫu thức khác 0.
5x21z không là phân thức vì mẫu số không là đa thức.
x2+2√x−90.yz không là đa thức vì mẫu số bằng 0.
Đáp án B.
Số phát biểu đúng trong các câu sau:
(i) Phân thức đại số là biểu thức có dạng PQ với Q và P là những đa thức.
(ii) Nếu hai phân thức bằng nhau AB=CD thì A⋅D=B⋅C
(iii) Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác 0 thì được một phân thức bằng phân thức đã cho.
Đáp án : B
Dựa vào khái niệm phân thức, hai phân thức bằng nhau và tính chất cơ bản của phân thức.
Phân thức đại số là biểu thức có dạng PQ với Q và P là những đa thức, Q≠0
Nếu hai phân thức bằng nhau AB=CD thì A⋅D=B⋅C
Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác 0 thì được một phân thức bằng phân thức đã cho.
Nếu chia cả tử và mẫu của một phân thức cho một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.
Đáp án B.
Cho ΔABC∽ΔA′B′C′, biết ˆA=600,^B′=500. Khi đó:
Đáp án : C
Hai tam giác đồng dạng thì hai tam giác có tất cả các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ.
Áp dụng định lí tổng ba góc trong tam giác bằng 1800
Vì ΔABC∽ΔA′B′C′ nên
{ˆA=^A′=600ˆB=^B′=600ˆC=^C′
Suy ra ˆC=^C′=1800−^A′−^B′=1800−600−500=700
Đáp án C.
Cho hình thang ABCD(AB∥CD) có ^ABD=^BDC,AB=2cm,BD=√5, ta có:
Đáp án : D
TH đồng dạng g-g: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Suy ra các cạnh tương ứng tỉ lệ.
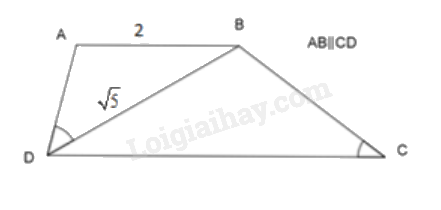
Vì AB∥CD nên: ^ABD=^BDC (cặp góc so le trong)
Xét ΔADB và ΔBCD ta có:
^ABD=^BDC(cmt)^ADB=^BCD(theogt)
Suy ra ΔADB∽ΔBCD(g−g)
Do đó ABBD=DBCD
2√5=√5CDCD=√5⋅√52=52=2,5cm
Đáp án D.
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
Đáp án : B
Phương trình nào sau đây là phương trình bậc nhất một ẩn có dạng ax+b=0(a≠0)
7x−9=0 là phương trình bậc nhất một ẩn
Đáp án B.
Cho ΔABC và ΔXYZ đồng dạng. A tương ứng với X,B tương ứng với Y.B biết AB=3, BC=4 và XY=5. Tính YZ ?
Đáp án : D
Từ cặp tam giác đồng dạng tìm ra tỉ lệ thức phù hợp, từ đó tìm ra độ dài của YZ.
Theo bài ta có: ΔABC∽ΔXYZ suy ra
ABXY=BCYZ35=4YZ
Suy ra YZ=5.43=203=623
Đáp án D.
Một người đi ô tô từ A đến B với tốc độ 45km/h. Khi đến B, người đó nghỉ 30 phút rồi quay về A với tốc độ 40km/h. Tính quãng đường AB, biết tổng thời gian đi, thời gian về và thời gian nghỉ là 4 giờ 45 phút.
Đáp án : B
Bước 1. Lập phương trình.
Bước 3. Trả lời.
Đổi: 4 giờ 45 phút =194 giờ; 30 phút =12 giờ.
Gọi quãng đường AB là x(km). Điều kiện: x>0.
Thời gian ô tô đi từ A đến B là: x45 (giờ).
Thời gian ô tô đi từ B về A là: x40 (giờ).
Vi tổng thời gian đi, thời gian về và thời gian nghỉ là 4 giờ 45 phút nên ta có PT:
x45+x40+12=1948x360+9x360=194−1217x360=174x=90(TM)
Vậy quãng đường AB dài 90km.
Đáp án B.
Giải phương trình sau 13x+12=x+2 ta được:
Đáp án : B
- Chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó (Quy tắc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
13x+12=x+2
13x−x=2−12
−23x=32
x=32⋅−32
x=−94
Đáp án B.
Tìm phân thức đối của kết quả phép chia 3x+15x2−4:x+5x−2 sau khi thu gọn.
Đáp án : B
Muốn chia phân thức AB cho phân thức CD khác 0 , ta nhân AB với phân thức nghịch đảo của CD
AB:CD=AB⋅DC
Phân thức đối của phân thức AB kí hiệu là −AB
3x+15x2−4:x+5x−2=3x+15x2−4⋅x−2x+5=3(x+5)(x−2)(x+2)⋅x−2x+5=3x+2
Phân thức đối của 3x+2 là −3x+2
Đáp án B.
Để đo khoảng cách giữa hai địa điểm D, E ở hai bên bờ của một con sông, người ta chọn các vị trí A,B,C ở cùng một bên bờ với điểm D và đo được AB=2m,AC=3m,CD=15m. Giả sử ΔABC∽ΔDEC. Tính khoảng cách DE.
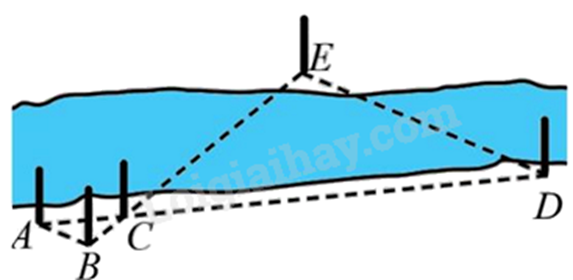
Đáp án : B
Nếu ΔABC∽ΔA′B′C′, ta có tỉ số các cạnh tương ứng A′B′AB=B′C′BC=C′A′CA=k gọi là tỉ số đồng dạng.
Vì ΔABC∽ΔDEC suy ra
23=DE15DE=23⋅15=10m
Vậy DE=10m
Đáp án B.
Giải các phương trình sau:
a) 7x−21=0;
b) 5x−x+20=0;
c) 23x+2=13
d) 32(x−54)−58=x.
- Chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó (Quy tắc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
a) 7x−21=0
7x=21
x=3
Vậy x=3
b) 5x−x+20=0
4x=−20
x=−5
Vậy x=−5
c) 23x+2=13
23x=13−2
23x=−53x=−53⋅32
x=−52
Vậy x=−52
d) 32(x−54)−58=x.
32x−158−58=x
32x−x=58+158
12x=52
x=5
Vậy x=5
Cho biểu thức P=x2+3xx2+6x+9+3x−3+x9−x2
a) Rút gọn biểu thức đã cho
b) Tính giá trị của biểu thức tại x=−2
Thu gọn biểu thức bằng cách thực hiện phép cộng các phân thức đại số: Muốn cộng hai hay nhiều phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu vừa tìm được.
Thay giá trị của biến vào biểu thức ta được giá trị của phân thức.
a) P=x2+3xx2+6x+9+3x−3+x9−x2
=x(x+3)(x+3)2+3x−3+−6xx2−9
=xx+3+3x−3+−6x(x+3)(x−3)
=x(x−3)+3(x+3)−6x(x+3)(x−3)
=x2−3x+3x+9−6x(x+3)(x−3)
=(x−3)2(x+3)(x−3)
=x−3x+3
b) Tại x=−2 ta có P=−2−3−2+3=−51=−5
Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất 50 sản phẩm. Khi thực hiện, mỗi ngày tổ sản xuất 57 sản phẩm. Do đó, tổ đã hoàn thành trước kế hoạch 1 ngày và còn vượt mức 13 sản phẩm. Hỏi theo kế hoạch, tổ phải sản xuất bao nhiêu sản phẩm?
Bước 1. Lập phương trình.
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
- Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời.
- Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không.
- Kết luận.
Gọi số sản phẩm phải sản xuất theo kế hoạch là x (sản phẩm). Điều kiện: x∈N∗,x>50.
Số sản phẩm thực tế sản xuất được là: x+13 (sản phẩm).
Thời gian hoàn thành công việc theo kế hoạch là: x50 (ngày).
Thời gian hoàn thành công việc thực tế là: x+1357 (ngày).
Vì thực tế tổ đã hoàn thành trước kế hoạch 1 ngày nên ta có PT:
x50−x+1357=157x−50(x+13)50.57=157x−50x−650=50.577x=2850+6507x=3500x=500(TM)
Vậy theo kế hoạch tổ phải sản xuất 500 sản phẩm.
Cho tam giác ABC với AB=6cm,AC=9cm.
a) Lấy các điểm M,N lần lượt trên các cạnh AB,AC sao cho AM=4cm,AN=6cm. Chứng minh rằng ΔAMN∽ΔABC và tìm tỉ số đồng dạng.
b) Lấy điểm P trên cạnh AC sao cho AP=4cm. Chứng minh rằng ΔAPB∽ΔABC.
a) Áp dụng định lí Thales đảo chứng minh MN/ /BC
Áp dụng định lí: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
b) Chứng minh ΔAPB=ΔAMN(c−g−c). Suy ra đpcm.
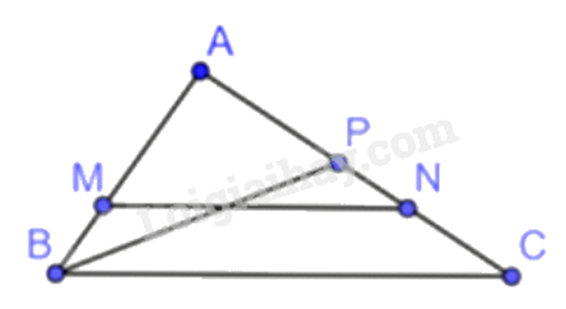
a) Xét ΔABC có: AMAB=ANAC(46=69=23)
nên MN//BC (định lí Thales đảo)
Suy ra ΔAMN∽ΔABC (định lí) với tỉ số đồng dạng 23
b) Xét ΔAPB và ΔAMN có: AP=AM(=4cm),ˆA chung, AB=AN(=6cm)
Suy ra ΔAPB=ΔAMN(c−g−c)(2)
Từ (1) và (2) suy ra ΔAPB∽ΔABC
Tính A=yz(x−y)(x−z)+zx(y−z)(y−x)+xy(z−x)(z−y)
Biến đổi phân thức đại số.
Sử dụng phương pháp phân tích đa thức thành nhân tử.
A=yz(x−y)(x−z)+zx(y−z)(y−x)+xy(z−x)(z−y)
=−yz(y−z)−zx(z−x)−xy(x−y)(x−y)(y−z)(z−x)
=−y2z+z2−z2x+x2z−x2y+x2(x−y)(y−z)(z−x)
=−y2(z−x)+y(z2−x2)−zx(z−x)(x−y)(y−z)(z−x)
=(z−x)(−y2+yz+yx−zx)(x−y)(y−z)(z−x)
=(z−x)[−y(y−z)+x(y−z)](x−y)(y−z)(z−x)
=(z−x)(y−z)(x−y)(x−y)(y−z)(z−x)=1
Vậy A = 1
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365