Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 8 - Kết nối tri thức
Đề thi giữa kì 2 Toán 8 - Đề số 8 - Kết nối tri thức
Đề cương ôn tập học kì 2 Toán 8 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 7 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 6 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 5 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 4 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 3 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 2 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 1 - Kết nối tri thứcĐề thi giữa kì 2 Toán 8 - Đề số 8 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Câu 1: Một tàu du lịch đi từ Hải Phòng đến Quảng Ninh với quang đường dài
Một tàu du lịch đi từ Hải Phòng đến Quảng Ninh với quang đường dài 50km/h. Vận tốc của dòng nước là 3km/h. Gọi vận tốc thực của tàu là xkm/h. Hãy biểu diễn thời gian tàu đi ngược dòng từ Quảng Ninh tới Hải Phòng.
Đáp án : A
Sử dụng công thức bài toán chuyển động dòng nước sau đó thiết lập biểu thức theo yêu cầu.
Vận tốc ngược dòng của tàu đi từ Quảng Ninh đến Hải Phòng là: x−3(km/h)
Thời gian tàu đi ngược dòng từ Quảng Ninh đến Hải Phòng là: 50x−3 (giờ)
Đáp án A.
Quan sát hình sau và chỉ ra một cặp tam giác đồng dạng:
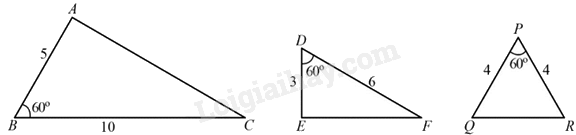
Đáp án : D
TH đồng dạng thứ hai (c-g-c): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Xét ΔABC và ΔEDF có: {^ABC=^EDF=600ABBC=DEEF=12 suy ra ΔABC∽ΔEDF (c.g.c)
Đáp án D.
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
Đáp án : D
Phương trình dạng ax+b=0, với a và b là hai số đã cho và a≠0, được gọi là phương trình bậc nhất một ân.
Các phương trình 3x+35=0,23y−7=0,7=2t có dạng nên là phương trình bậc nhất một ẩn.
Phương trình z2−9=0 có bậc hai nên không là phương trình bậc nhất một ẩn
Đáp án D.
Điều kiện xác định của phân thức (x−1)(x+3)x2−1 là:
Đáp án : C
Điều kiện xác định của phân thức là mẫu thức khác 0 .
Điều kiện xác định của phân thức (x−1)(x+3)x2−1 là: x2−1≠0 hay x≠1,x≠−1
Đáp án C.
Chọn khẳng định sai.
Đáp án : B
Nhận biết hai tam giác đồng dạng.
Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1
Hai tam giác đều có các góc đều bằng 600 và các cạnh tương ứng tỉ lệ nên chúng đồng dạng.
Hai tam giác cân chưa chắc đồng dạng nên B sai.
Đáp án B.
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
Đáp án : B
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Ta thấy:
412=515=618=13 nên A đúng.
39=412≠616 nên B sai.
21=21=21 nên C đúng.
147=157,5=168=2 nên D đúng
Đáp án B.
Kết quả của phép chia a−2b16:2a−4b12 bằng:
Đáp án : A
Muốn chia phân thức AB cho phân thức CD khác 0 , ta nhân AB với phân thức nghịch đảo của CD
AB:CD=AB⋅DC
a−2b16:2a−4b12=a−2b16⋅122a−4b=(a−2b)⋅1216⋅(2a−4b)=(a−2b)⋅1232⋅(a−2b)=38
Đáp án A.
Nếu 2 tam giác ABC và DEF có ˆA=ˆD,ˆC=ˆF thì:
Đáp án : A
TH đồng dạng g-g: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Xét ΔABC và ΔDEF có: ˆA=ˆD(gt);ˆC=ˆF(gt)
Suy ra ΔABC∽ΔDEF(g−g)
Đáp án A.
Tổng các nghiệm của hai phương trình −6(1,5−2x)=3(−15+2x);5x+10=0 bằng:
Đáp án : A
Giải lần lượt từng phương trình:
PT1: −6(1,5−2x)=3(−15+2x)
−2(1,5−2x)=−15+2x
−3+4x=−15+2x
4x−2x=−15+3
2x=−12
x=−6
PT2: 5x+10=0
5x=−10
x=−2
Ta có tổng các nghiệm của hai phương trình trên là −6+(−2)=−8
Đáp án A.
Cho biết một nửa đàn bò đang gặm cỏ trên cánh đồng, 13 đàn bò đang nằm nghỉ gần đó, còn lại 4 con đang uống nước ở ao. Tính số bò hiện có trong đàn.
Đáp án : C
Bước 1. Lập phương trình.
Bước 3. Trả lời.
Gọi số bò có trong đàn là x (con). Điều kiện: x∈N∗.
Vì một nửa đàn bò đang gặm cỏ trên cánh đồng, 13 đàn bò đang nằm nghỉ gần đó, còn lại 4 con đang uống nước ở ao nên ta có PT:
12x+13x+4=x
x−12x−13x=4
16x=4
x=24(TM)
Vậy đàn bò có 24 con.
Đáp án C.
Cho biểu thức: B=1x+1−x3−xx2+1⋅(1x2+2x+1−1x2−1) (ĐKXĐ: x≠±1)
a) Rút gọn B
b) Tính giá trị của B tại x=−2
c) Với giá trị nào của x thì B=1
Rút gọn biểu thức bằng cách thực hiện các phép toán cộng, trừ, nhân, chia phân thức.
Tính giá trị của biểu thức tại giá trị của biến cho trước.
Tìm giá trị của biến tại giá trị của biểu thức cho trước.
a) B=1x+1−x(x−1)(x+1)x2+1⋅(x−1)−(x+1)(x+1)2(x−1)( ĐКXĐ: x≠±1)
B=1x+1−−2x(x2+1)(x+1)
B=x2+1+2x(x2+1)(x+1)
B=(x+1)2(x2+1)(x+1)
B=x+1x2+1
Vậy B=x+1x2+1 với x≠±1
b) Thay x=−2 (TM) ta có: B=−2+1(−2)2+1=−15
c) B=1⇒x+1x2+1=1⇔x+1=x2+1⇔x−x2=0⇔x(1−x)=0⇔[x=0(TM)x=1(KTM)
Vậy khi x=0 thì B=1
Giải các phương trình sau:
a) 9x+56=1−6+3x8;
b) x+14=12+2x+15;
c) 2(x+1)3=32−1−2x4.
- Chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó (Quy tấc chuyển vế);
- Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số);
- Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số).
a) 9x+56=1−6+3x8
4(9x+5)24=2424−3(6+3x)24
36x+20=24−18−9x
36x+9x=6−20
45x=−14
x=−1445
Vậy x=−1445
b) x+14=12+2x+15
5(x+1)20=1020+4(2x+1)5
5x+5=10+8x+4
5x−8x=14−5
−3x=9
x=−3
Vậy x=−3
c) 2(x+1)3=32−1−2x4
8(x+1)12=1812−3(1−2x)12
8x+8=18−3+6x
8x−6x=15−8
2x=7
x=72
Vậy x=72
Tổng số học sinh khối 8 và khối 9 của một trường là 580 em, trong đó có 256 em là học sinh giỏi. Tính số học sinh của mỗi khối, biết rằng số học sinh giỏi khối 8 chiếm tỉ lệ 40% số học sinh khối 8, số học sinh giỏi khối 9 chiếm tỉ lệ 48% số học sinh khối 9.
Bước 1. Lập phương trình.
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết.
- Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Trả lời.
- Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không.
- Kết luận.
Gọi số học sinh khối 8 là x. (học sinh). Điều kiện: x∈N∗;x<580.
Số học sinh khối 9 là: 580−x (học sinh).
học sinh giỏi khối 8 là: 40%x=0,4x (học sinh)
Số học sinh giỏi khối 9 là: 48 (học sinh)
Vì cả hai khối có tổng cả 256 học sinh giỏi nên ta có phương trình:
0,4x+0,48(560−x)=256
0,4x+268,8−0,48x=256
0,4x−0,48x=256−268,8
−0,08x=−12,8
x=(−12,8):(−0,08)
x=160(tm)
Khi đó, số học sinh khối 9 là: 580−160=420 (học sinh)
Vậy khối 8 có 160 học sinh và khối 9 có 420 học sinh.
Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Chứng minh:
a) ΔHBE đồng dạng với ΔHCD.
b) ^HDE=^HAE.
Chứng minh các cặp tam giác đồng dạng, từ đó rút ra dữ kiện cần thiết để chứng minh yêu cầu của bài toán.
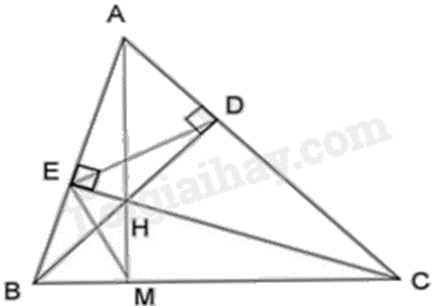
a) Xét ΔHBE và ΔHCD có:
^BDC=^CEB=900
^EHB=^DHC (2 góc đối đỉnh)
Suy ra ΔHBE∽ΔHCD(g−g) (điều phải chứng minh)
b) Theo câu a) ta có: ΔHBE∽ΔHCD suy ra HEHD=HBHC hay HEHB=HDHC
Xét ΔHED và ΔHBC ta có:
HEHB=HDHC (cmt)
^EHD=^BHC (hai góc đối đỉnh)
^HDE=^HAE
Suy ra ΔHED∽ΔHBC(c−g−c).
Mà đường cao BD và CE cắt nhau tại H (theo giả thiết)
Suy ra H là trực tâm của ΔABC hay AH⊥BC tại M suy ra ^AMB=90∘.
Xét ΔAMB và ΔCEB có:
^CEB=^AMB=900
ˆB chung
Suy ra ΔAMB∽ΔCEB(g−g)
Suy ra ^MAB=^ECB hay ^HAE=^HCB (2)
Từ (1) và (2) ta có: ^HDE=^HAE (điều phải chứng minh)
Cho ab+c+bc+a+ca+b=1. Chứng minh a2b+c+b2c+a+c2a+b=0
Nhân cả 2 vế của ab+c+bc+a+ca+b=1 với a+b+c rồi thu gọn được điều phải chứng minh
Nhân cả 2 vế của ab+c+bc+a+aa+b=1 với a+b+c ta được
a(a+b+c)b+c+b(a+b+c)c+a+c(a+b+c)a+b=a+b+c
a2+a(b+c)b+c+b2+b(c+a)c+a+c2+c(a+b)a+b=a+b+c
a2b+c+a+b2c+a+b+c2a+b+c=a+b+c
a2b+c+b2c+a+c2a+b=0(dpcm)
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365