Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 8 - Kết nối tri thức
Đề thi giữa kì 2 Toán 8 - Đề số 5 - Kết nối tri thức
Đề thi giữa kì 2 Toán 8 - Đề số 6 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 7 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 8 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 4 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 3 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 2 - Kết nối tri thức Đề thi giữa kì 2 Toán 8 - Đề số 1 - Kết nối tri thứcĐề thi giữa kì 2 Toán 8 - Đề số 5 - Kết nối tri thức
Phần trắc nghiệm (2 điểm) Câu 1: Phân thức (frac{2}{x-3}) không có nghĩa khi:
Phân thức 2x−3 không có nghĩa khi:
Đáp án : A
Phân thức AB có nghĩa khi B≠0 nên phân thức AB không có nghĩa khi B=0.
Phân thức 2x−3 có nghĩa khi x−3=0 hay x=3.
Cho (x+y)2x−y=Px2−y2. Đa thức P là:
Đáp án : C
Sử dụng kiến thức về hai phân thức bằng nhau.
Ta có: (x+y)2x−y=Px2−y2
⇒(x+y)2.(x2−y2)=P.(x−y)(x+y)2.(x+y)(x−y)=P.(x−y)(x+y)3(x−y)=P(x−y)⇒P=(x+y)3
Rút gọn phân thức x3−2x22x2−4x ta được
Đáp án : C
Thực hiện rút gọn phân thức theo 2 bước:
+ Bước 1: Phân tích tử và mẫu thành nhân tử (nếu cần).
+ Bước 2: Tìm nhân tử chung của tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó.
Ta có: x3−2x22x2−4x=x2(x−2)2x(x−2)=x2.
Thương của hai phân thức 2xx−3 và 4x23−x là:
Đáp án : B
Sử dụng quy tắc chia hai phân thức.
Ta có: 2xx−3:4x23−x=2xx−3.3−x4x2=2xx−3.−(x−3)4x2=−2x4x2=−12x.
Cho hình vẽ sau, giá trị của x là:
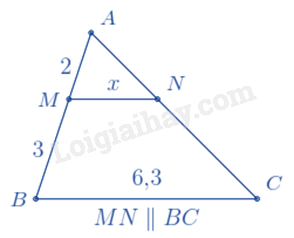
Đáp án : A
Dựa vào định lí hai tam giác đồng dạng.
Ta có: MN // BC nên ΔAMN∽ (định lí hai tam giác đồng dạng)
\Rightarrow \frac{{AM}}{{AB}} = \frac{{MN}}{{BC}} \Rightarrow \frac{2}{{2 + 3}} = \frac{x}{{6,3}} \Rightarrow x = 6,3.\frac{2}{5} = 2,52.
Cho ABC có AB = 24cm, AC = 30cm, BC = 36cm . Trên cạnh AB lấy E sao cho AE = 20cm . Trên cạnh AC lấy F sao cho AF = 16cm. Độ dài cạnh EF là
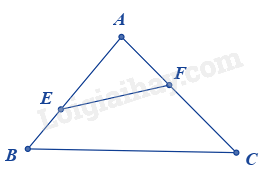
Đáp án : C
Chứng minh \Delta AEF\backsim \Delta ACB suy ra tỉ số đồng dạng.
Xét \Delta AEF và \Delta ACB có:
\widehat A chung
\frac{{AE}}{{AF}} = \frac{{AC}}{{AB}}\left( {\frac{{20}}{{16}} = \frac{{30}}{{24}} = \frac{5}{4}} \right)
\Rightarrow \Delta AEF\backsim \Delta ACB\left( c.g.c \right)
\begin{array}{l}\frac{{AE}}{{AC}} = \frac{{EF}}{{BC}}\\\frac{{20}}{{30}} = \frac{{EF}}{{36}}\\ \Rightarrow EF = 36.\frac{{20}}{{30}} = 24\end{array}
Ông An có một khu vườn, trong đó có miếng đất dạng hình tam giác vuông ABC như hình vẽ bên. Biết M là trung điểm của BC; AC = 40m; AM = 25m. Ông muốn trang trí lại khu vườn của mình nên cần biết khoảng cách từ A đến B. Em hãy giúp ông tính khoảng cách từ A đến B.
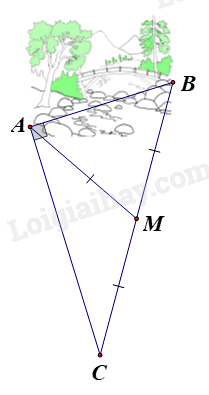
Đáp án : C
Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác để tính BC, định lí Pythagore để tính AB.
Vì tam giác ABC vuông tại A và M là trung điểm của BC nên AM là đường trung tuyến ứng với cạnh huyền trong tam giác ABC.
\Rightarrow AM = \frac{1}{2}BC \Rightarrow BC = 2AM = 2.25 = 50\left( m \right)
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
\begin{array}{l}A{B^2} = B{C^2} - A{C^2} = {50^2} - {40^2} = {30^2}\\ \Rightarrow AB = 30\left( m \right)\end{array}
Cho \Delta ABC\backsim \Delta HIK, biết \widehat A = {80^0},\widehat B = {25^0}. Khi đó số đo \widehat K bằng
Đáp án : C
Sử dụng đặc điểm của hai tam giác đồng dạng.
Vì \Delta ABC\backsim \Delta HIK nên \widehat A = \widehat H;\widehat B = \widehat I;\widehat C = \widehat K
\Rightarrow \widehat C = \widehat K = {180^0} - \widehat A - \widehat B = {180^0} - {80^0} - {25^0} = {75^0}.
1. Một vườn cây có {x^2} + 2x - {y^2} - 2y cây, trong đó có {x^2} - {y^2} cây lấy gỗ còn lại là cây ăn quả.
a) Viết phân thức biểu thị tỉ số cây lấy gỗ và số cây ăn quả.
b) Tính giá trị của phân thức đó tại x = 100;y = 10.
2. Thực hiện phép tính:
a) \frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x - 4{x^2}}}
b) \frac{{{x^2} + x}}{{5{x^2} - 10x + 5}}:\frac{{3x + 3}}{{5x - 5}}
1. Sử dụng quy tắc trừ đa thức để tính số cây ăn quả.
a) Viết phân thức có số cây lấy gỗ là tử và số cây ăn quả là mẫu.
b) Thay x = 100 và y = 10 vào phân thức để tính giá trị.
2. Sử dụng các quy tắc tính với phân thức để tính.
1. Số cây ăn quả là:
\begin{array}{l}{x^2} + 2x - {y^2} - 2y - \left( {{x^2} - {y^2}} \right)\\ = {x^2} + 2x - {y^2} - 2y - {x^2} + {y^2}\\ = \left( {{x^2} - {x^2}} \right) + \left( { - {y^2} + {y^2}} \right) + 2x - 2y\\ = 2x - 2y\end{array}
a) Phân thức biểu thị tỉ số cây lấy gỗ và số cây ăn quả là: \frac{{{x^2} - {y^2}}}{{2x - 2y}}.
b) Ta có: \frac{{{x^2} - {y^2}}}{{2x - 2y}} = \frac{{\left( {x - y} \right)\left( {x + y} \right)}}{{2\left( {x - y} \right)}} = \frac{{x + y}}{2}.
Thay x = 100;y = 10 vào phân thức ta được: \frac{{100 + 10}}{2} = \frac{{110}}{2}.
2.
a) \frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x - 4{x^2}}} (ĐK: x \ne 0;x \ne \frac{1}{2})
\begin{array}{l} = \frac{{1 - 3x}}{{2x}} + \frac{{3x - 2}}{{2x - 1}} + \frac{{3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{\left( {1 - 3x} \right)\left( {1 - 2x} \right)}}{{2x\left( {1 - 2x} \right)}} - \frac{{2x\left( {3x - 2} \right)}}{{2x\left( {1 - 2x} \right)}} + \frac{{3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{1 - 5x + 6{x^2} - 6{x^2} + 4x + 3x - 2}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{2x - 1}}{{2x\left( {1 - 2x} \right)}}\\ = \frac{{ - 1}}{{2x}}\end{array}
b) \frac{{{x^2} + x}}{{5{x^2} - 10x + 5}}:\frac{{3x + 3}}{{5x - 5}} (ĐK: x \ne 1)
\begin{array}{l} = \frac{{x\left( {x + 1} \right)}}{{5\left( {{x^2} - 2x + 1} \right)}}.\frac{{5\left( {x - 1} \right)}}{{3\left( {x + 1} \right)}}\\ = \frac{{x\left( {x + 1} \right).5\left( {x - 1} \right)}}{{5{{\left( {x - 1} \right)}^2}.3\left( {x + 1} \right)}}\\ = \frac{x}{{3\left( {x - 1} \right)}}\end{array}
Cho các biểu thức P = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2x + 10}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}; Q = \frac{{x - 4}}{{{x^2} - 25}} với x \ne \pm 5.
a) Tính giá trị Q với x = 6.
b) Rút gọn biểu thức P.
c) Đặt A = \frac{Q}{P}. Tìm các giá trị nguyên của x để A nhận giá trị nguyên.
a) Kiểm tra điều kiện của x, nếu thỏa mãn thì thay giá trị của x vào Q để tính Q.
b) Sử dụng các quy tắc tính với phân thức để rút gọn P.
c) Tính A = \frac{Q}{P}. Để A nguyên thì tử thức chia hết cho mẫu thức.
a) Ta có x = 6 thỏa mãn điều kiện nên thay x = 6 vào Q, ta được:
Q = \frac{{6 - 4}}{{{6^2} - 25}} = \frac{2}{{11}}
Vậy Q = \frac{2}{{11}} với x = 6.
b) Ta có:
\begin{array}{l}P = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2x + 10}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\\ = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{{2\left( {x + 5} \right)}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\\ = \frac{1}{{x + 5}} + \frac{2}{{x - 5}} - \frac{2}{{x - 5}}\\ = \frac{1}{{x + 5}}\end{array}
Vậy P = \frac{1}{{x + 5}}.
c) Ta có:
\begin{array}{l}A = \frac{Q}{P} = \frac{1}{{x + 5}}:\frac{{x - 4}}{{{x^2} - 25}}\\ = \frac{1}{{x + 5}}.\frac{{\left( {x - 5} \right)\left( {x + 5} \right)}}{{x - 4}}\\ = \frac{{x - 5}}{{x - 4}}\end{array}
A = \frac{{x - 5}}{{x - 4}} = \frac{{x - 4 - 1}}{{x - 4}} = 1 - \frac{1}{{x - 4}}.
Để A nguyên thì \frac{1}{{x - 4}} là số nguyên hay 1 \vdots \left( {x - 4} \right) \Rightarrow \left( {x - 4} \right) \in Ư(1); Ư(1) = \left\{ { \pm 1} \right\}.
Với x – 4 = 1 \Rightarrow x = 5 (không thỏa mãn)
Với x – 4 = -1 \Rightarrow x = 3 (thỏa mãn)
Vậy với x = 3 thì A nguyên.
Cho hình vẽ bên. Tính chiều dài của cánh buồm?

(Làm tròn đến hàng phần trăm).
Áp dụng Định lí Pythagore để tính chiều dài của cánh buồm.
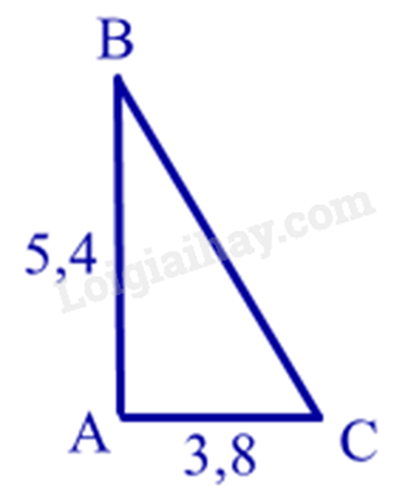
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
\begin{array}{l}B{C^2} = A{B^2} + A{C^2} = 5,{4^2} + 3,{8^2} = 43,6\\ \Rightarrow BC = 6,60\end{array}
Vậy chiều dài cánh buồm là 6,6.
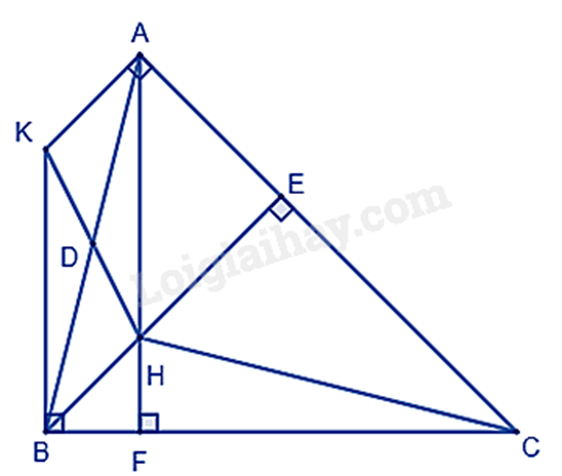
Cho tam giác ABC có ba góc nhọn. Đường cao AF, BE cắt nhau tại H. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By vuông góc với BC. Tia Ax và By cắt nhau tại K.
a) Tứ giác AHBK là hình gì? Vì sao?
b) Chứng minh \Delta HAE\backsim \Delta HBF.
c) Chứng minh CE.CA = CF.CB.
d) \Delta ABC cần thêm điều kiện gì để tứ giác AHBK là hình thoi.
a) Chứng minh AHBK có hai cặp cạnh đối song song nên là hình bình hành.
b) Chứng minh \Delta HAE\backsim \Delta HBF theo trường hợp góc – góc.
c) Chứng minh \Delta AFC\backsim \Delta BEC (g.g) để chứng minh CE.CA = CF.CB.
d) Gọi D là giao điểm KH và AB
Để tứ giác AHBK là hình thoi thì KH vuông góc AB
Ta có: H là trực tâm \Rightarrow CH vuông góc AB
\Rightarrow C, H, D thẳng hàng \Rightarrow CD là đường cao và D là trung điểm của AB \Rightarrow CD cũng là đường trung tuyến
\Rightarrow Tam giác ABC cân tại C
a) Ta có:
\left. \begin{array}{l}AK \bot AC\\BE \bot AC\end{array} \right\} \Rightarrow AK//BE
\left. \begin{array}{l}BK \bot BC\\AF \bot BC\end{array} \right\} \Rightarrow BK//AF
Xét tứ giác AHBK có:
\begin{array}{l}AK//BH\left( {H \in BE} \right)\\AB//AH\left( {H \in AF} \right)\end{array}
\Rightarrow AHBK là hình bình hành.
b) Xét \Delta HAE và \Delta HBF có:
\widehat E = \widehat F\left( { = {{90}^0}} \right)
\widehat {AHE} = \widehat {BHF} (hai góc đối đỉnh)
\Rightarrow \Delta HAE\backsim \Delta HBF (g.g) (đpcm)
c) Xét \Delta AFC và \Delta BEC có:
\widehat F = \widehat E\left( { = {{90}^0}} \right)
\widehat C chung
\Rightarrow \Delta AFC\backsim \Delta BEC\left( g.g \right)
\Rightarrow \frac{{AC}}{{BC}} = \frac{{CF}}{{CE}} \Rightarrow AC.CE = CF.CB (đpcm)
d) Gọi D là giao điểm của AB và HK \Rightarrow D là trung điểm của AB và HK.
Để AHBK là hình thoi thì AB \bot HK.
Mà H trực tâm của tam giác ABC nên CH \bot AB.
\Rightarrow C, H, K thẳng hàng hay C, H, D thẳng hàng.
Khi đó CD là đường cao của tam giác ABC.
Mà D là trung điểm của AB nên CD cũng là đường trung tuyến của tam giác ABC
\Rightarrow Tam giác ABC cân tại C.
Vậy để AHBK là hình thoi thì tam giác ABC cân tại C.
Cho a, b, c và x, y, z là các số khác nhau và khác 0. Chứng minh rằng:
Nếu \frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0 và \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 thì \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1.
Biến đổi \frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0 và \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 để có đpcm.
Sử dụng hằng đẳng thức nâng cao: {\left( {A + B + C} \right)^2} = {A^2} + {B^2} + {C^2} + 2AB + 2AC + 2BC.
Ta có:
\begin{array}{l}\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\\\frac{{ayz + bxz + cxy}}{{xyz}} = 0\\ \Rightarrow ayz + bxz + cxy = 0\end{array}
Ta lại có:
\begin{array}{l}\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\\ \Rightarrow {\left( {\frac{x}{a} + \frac{y}{b} + \frac{z}{c}} \right)^2} = 1\\{\left( {\frac{x}{a}} \right)^2} + {\left( {\frac{y}{b}} \right)^2} + {\left( {\frac{z}{c}} \right)^2} + 2.\frac{x}{a}.\frac{y}{b} + 2.\frac{x}{a}.\frac{z}{c} + 2.\frac{y}{b}.\frac{z}{c} = 1\\{\left( {\frac{x}{a}} \right)^2} + {\left( {\frac{y}{b}} \right)^2} + {\left( {\frac{z}{c}} \right)^2} + 2\left( {\frac{{xy}}{{ab}} + \frac{{xz}}{{ac}} + \frac{{yz}}{{bc}}} \right) = 1\\\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} + 2\left( {\frac{{xyc + bxz + ayz}}{{abc}}} \right) = 1\\\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} + 2.\frac{0}{{abc}} = 1\\\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\end{array}
Ta được điều phải chứng minh.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365