Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 8 - Chân trời sáng tạo
Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 9
Đề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 10 Đề thi giữa kì 2 Toán 8 - Đề số 8 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 7 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 6 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 5 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 4 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 3 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 2 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 8 - Đề số 1 - Chân trời sáng tạoĐề thi giữa kì 2 Toán 8 Chân trời sáng tạo - Đề số 9
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Các số lần lượt cần điền vào dấu “?” trong bảng sau là gì?
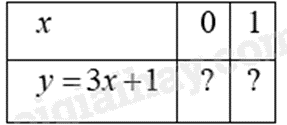
1;4.
4;4.
1;1.
4;1.
Đáp án : A
Thay giá trị x vào hàm số để tính giá trị của y tương ứng.
Với x=0, y=3.0+1=1.
Với x=1, y=3.1+1=4.
Đáp án A
Hệ số a, b trong hàm số bậc nhất y=4x−7 lần lượt là
4x;−7.
4x;7.
4;7.
4;−7.
Đáp án : D
Hàm số bậc nhất y=ax+b với hệ số a, b tương ứng.
Hàm số bậc nhất y=4x−7 có a=4;b=−7.
Đáp án D
Một ô tô cách thành phố Hồ Chí Minh 50km. Ô tô bắt đầu đi trên một con đường về phía ngược hướng với thành phố (hình vẽ) với vận tốc là 60km/h. Sau x giờ ô tô cách thành phố Hồ Chí Minh y km. Biểu diễn y theo x.
y=50x.
y=60x.
y=60x+50.
y=50x+60.
Đáp án : C
Vì ô tô đi về phía ngược hướng thành phố nên khoảng cách giữa ô tô và thành phố Hồ Chí Minh bằng khoảng cách ban đầu + quãng đường ô tô đi được.
Quãng đường = vận tốc x thời gian.
Quãng đường ô tô đi được trong x giờ là:
60x(km)
Sau x giờ ô tô cách thành phố Hồ Chí Minh là:
y=50+60x=60x+50
Đáp án C
Điểm nào sau đây thuộc đồ thị hàm số y=2x−4.
M(0;−4).
N(0;4).
P(4;0).
Q(−4;0).
Đáp án : A
Thay toạ độ điểm vào hàm số xem có thoả mãn không.
Thay x=0 vào y=2x−4, ta được: y=2.0−4=−4 nên M(0;−4) thuộc đồ thị hàm số y=2x−4, N(0;4) thuộc đồ thị hàm số y=2x−4.
Kiểm tra tương tự với P, Q.
Đáp án A
Cho mặt phẳng tọa độ Oxy và điểm A (như hình vẽ).
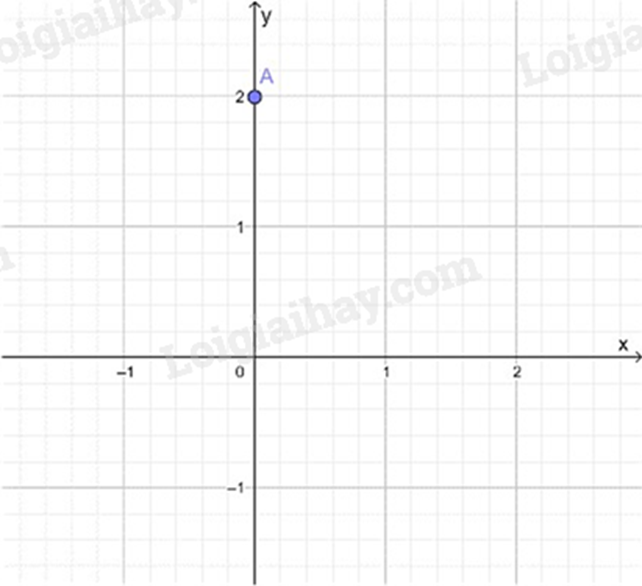
Khi đó tọa độ của điểm A là:
(0;0).
(2;2).
(2;0).
(0;2).
Đáp án : D
Quan sát đồ thị để trả lời.
Điểm A nằm trên trục tung, có hoành độ là 2 nên A(0;2).
Đáp án D
Hệ số góc của đường thẳng y=2x+12 là
1.
2.
2x.
12.
Đáp án : A
Hệ số góc của đường thẳng y=ax+b(a≠0) là a.
Ta có: y=2x+12=x+12.
Vậy hệ số góc của đường thẳng là 1.
Đáp án A
Cho hình vẽ: Đoạn thẳng nào là đường trung bình của tam giác ABC?
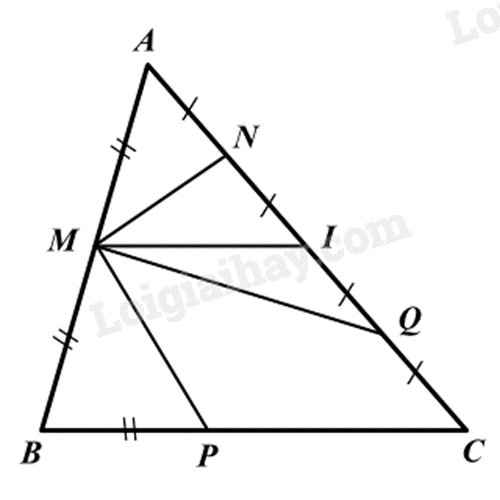
MP.
MN.
MI.
MQ.
Đáp án : C
Dựa vào khái niệm đường trung bình của tam giác: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Vì AN = NI = IQ = IC nên AN + NI = IQ + QC hay AI = IC
Xét tam giác ABC có:
AM = MB, AI = IC (M ∈ AB, I ∈ AC)
nên MI là đường trung bình của tam giác ABC.
Đáp án C
Cho tam giác ΔABC vuông tại A, biếtAB=6cm. Gọi M,N lần lượt là trung điểm của AB,AC và MN=5cm. Khi đó, độ dài AC là:
10cm.
3cm.
8cm.
11cm.
Đáp án : C
Chứng minh MN là đường trung bình của tam giác để suy ra BC.
Áp dụng định lí Pythagore vào tam giác vuông ABC để tính AC.
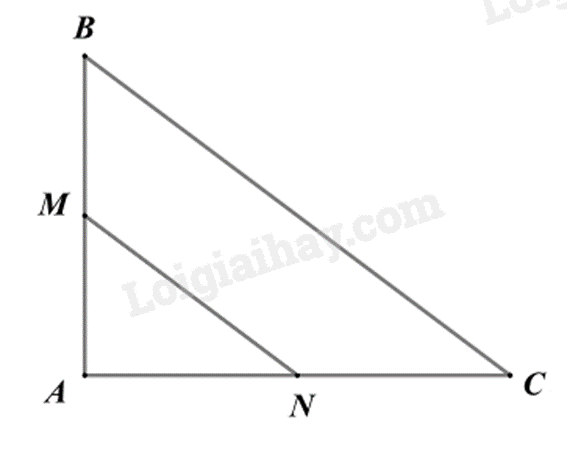
Xét tam giác ABC có:
M,N lần lượt là trung điểm của AB,AC nên MN là đường trung bình của tam giác ABC.
Do đó MN=12BC, suy ra BC=2MN=2.5=10(cm)
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
BC2=AB2+AC2
suy ra AC2=BC2−AB2=102−62=64, suy ra AC=√64=8(cm)
Đáp án C
Một cột đèn cao 10m chiếu sáng một cây xanh (như hình vẽ). Cây cách cột đèn 2m và có bóng trải dài dưới mặt đất là4,8m. Tìm chiều cao của cây xanh đó (làm tròn đến mét).
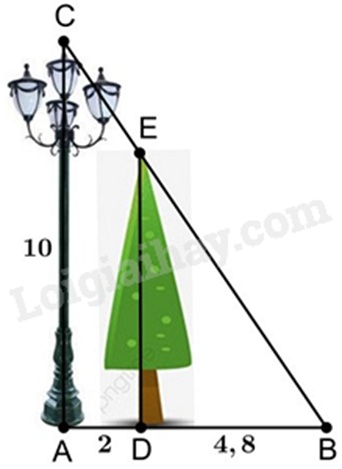
Khi đó, chiều cao của cây xanh là (làm tròn đến mét):
DE≈14m.
DE≈5m.
DE≈24m.
DE≈7m.
Đáp án : D
Sử dụng hệ quả của định lí Thalès: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Vì cột đèn và cây xanh cùng vuông góc với mặt đất nên chúng song song với nhau, hay DE // AC.
Suy ra BDAB=DEAC, hay BDAD+DB=DEAC
Thay số: 4,82+4,8=DE10, suy ra DE=4,8.106,8≈7(m)
Đáp án D
Cho ΔABC có AB=4cm;AC=9cm. Gọi AD là tia phân giác của ^BAC . Tính tỉ số CDBD.
94.
49.
45.
54.
Đáp án : A
Sử dụng Tính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
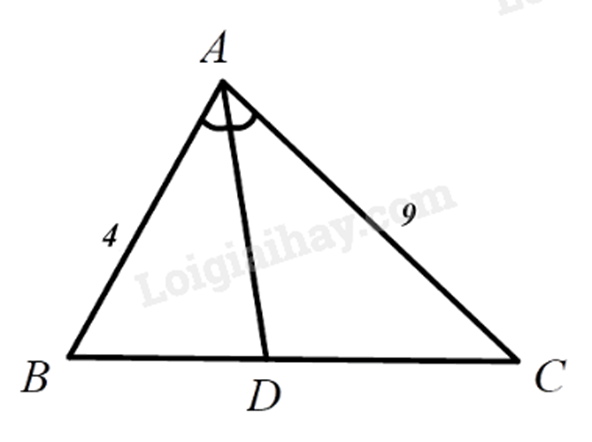
Vì AD là đường phân giác của tam giác ABC nên CDBD=ACAB=94.
Đáp án A
Cho ΔABC, tia phân giác góc trong của góc A cắt BC tại D. Cho AB=6, AC=x,BD=9,BC=21. Tính kết quả đúng của độ dài cạnh x?
x=14.
x=6.
x=12.
x=8.
Đáp án : D
Sử dụng Tính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
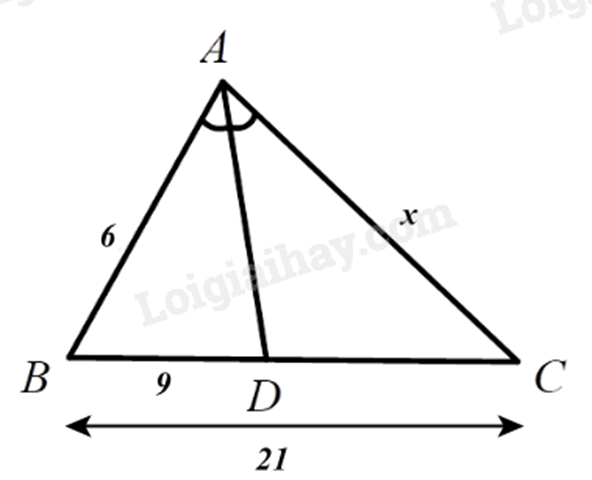
Vì D∈BC nên BD+DC=BC, suy ra CD=BC−BD=21−9=12.
Vì AD là đường phân giác của tam giác ABC nên ABAC=BDCD.
Thay số: 6x=912, suy ra x=6.129=8.
Đáp án D
Tìm x trong hình sau:
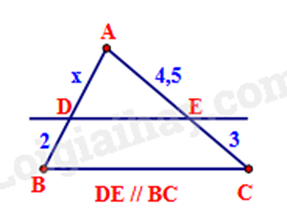
x = 4,5.
x = 3.
x = 1,33.
x = 6,75.
Đáp án : B
Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Vì DE // BC nên ADDB=AEEC
Thay số: x2=4,53, suy ra x=4,5.23=3.
Đáp án B
Cho hàm số y=(2−m)x+1
a) Với m=1 thì đồ thị hàm số song song với đường thẳng y=x.
b) Đồ thị hàm số với m=1 là:
c) Giao điểm A của đồ thị hàm số với m=1 và y=−x+3 là A(1;2).
d) Diện tích của tam giác OAB, với B là giao điểm của đồ thị hàm số y=−x+3 với trục Ox là 3.
a) Với m=1 thì đồ thị hàm số song song với đường thẳng y=x.
b) Đồ thị hàm số với m=1 là:

c) Giao điểm A của đồ thị hàm số với m=1 và y=−x+3 là A(1;2).
d) Diện tích của tam giác OAB, với B là giao điểm của đồ thị hàm số y=−x+3 với trục Ox là 3.
a) Thay m=1 vào hàm số. Hai đường thẳng y=ax+b(a≠0) và y=a′x+b′(a′≠0) song song nếu a=a′,b≠b′.
b) Vẽ đồ thị của hàm số để kiểm tra.
c) Tìm tọa độ giao điểm của hai đường thẳng theo các bước:
Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2: Thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số ta tìm được tung độ giao điểm.
d) Xác định độ dài đường cao và cạnh đáy của tam giác OAB để tính diện tích.
a) Đúng
Với m=1, phương trình trở thành: y=(2−1)x+1 hay y=x+1.
Vì y=x+1 và y=x có a=a′=1, b=1≠0=b′ nên đồ thị hàm số y=x+1 song song với đường thẳng y=x.
b) Sai
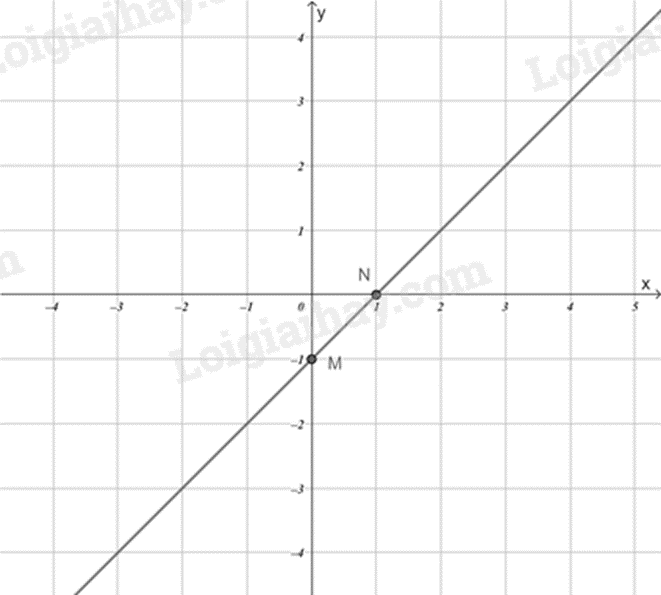
Với m=1, phương trình trở thành y=x+1.
+) Với x=0 thì y=0+1=1 nên đồ thị hàm số đi qua điểm M(0;1).
+) Với y=0 thì x=0−1=−1 nên đồ thị hàm số đi qua điểm N(−1;0).
Đồ thị hàm số y=x+1 là đường thẳng MN.
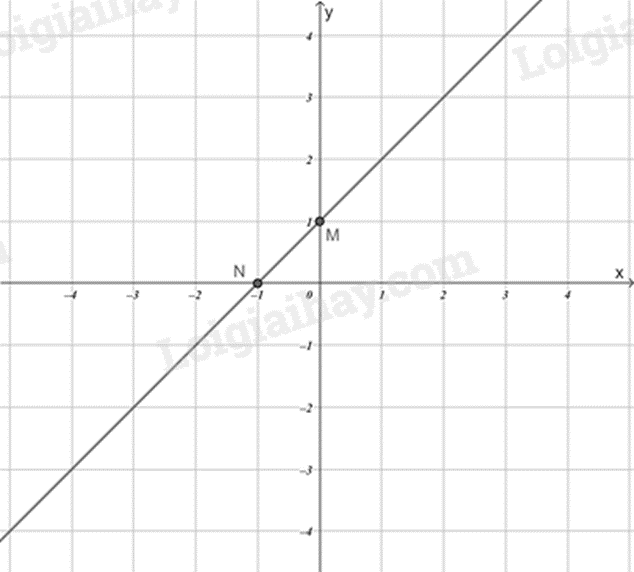
c) Đúng
Xét phương trình hoành độ giao điểm của hai đường thẳng y=x+1 và y=−x+3, ta được:
x+1=−x+3x+x=3−12x=2x=1
Khi đó y=1+1=2.
Vậy hoành độ giao điểm hai đường thẳng là A(1;2).
d) Đúng
Biểu diễn đồ thị hàm số y=−x+3 và y=x+1 trên cùng một mặt phẳng toạ độ.
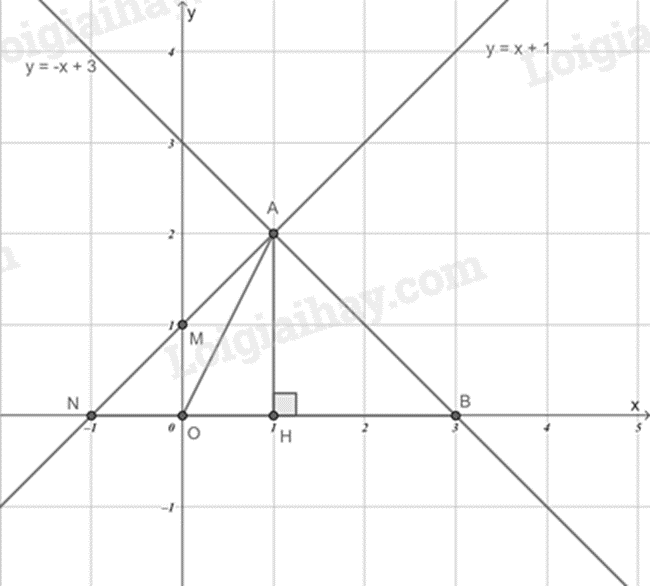
Với y=0, suy ra x=3 nên giao điểm của đồ thị hàm số y=−x+3 với trục Ox là B(3;0).
Kẻ AH⊥Ox, vì A có tung độ là 2 nên độ dài đoạn AH = 2.
Độ dài đoạn OB là 3.
Khi đó diện tích tam giác OAB là: SΔOAB=12.AH.OB=12.2.3=3.
Đáp án: ĐSĐĐ
Cho tam giác ABC vuông tại A có AB = 6cm. AC = 8cm. M, N là trung điểm của AB , AC. Vẽ AD là tia phân giác của góc A trong tam giác ABC (D thuộc BC).
a) BC = 10cm.
b) MN = 4cm.
c) BD≈4,5cm.
d) BD.AN=AM.DC.
a) BC = 10cm.
b) MN = 4cm.
c) BD≈4,5cm.
d) BD.AN=AM.DC.
a) Áp dụng định lí Pythagore vào tam giác ABC để tính BC.
b) Chứng minh MN là đường trung bình để tính MN.
c) Áp dụng tính chất đường phân giác trong tam giác để tính BD.
d) Kết hợp tính chất đường phân giác trong tam giác và tính chất của trung điểm của AB, AC để kiểm tra khẳng định.
a) Đúng
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
BC=√AB2+AC2=√62+82=10(cm)
b) Sai
Vì M, N là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC.
Suy ra MN=12BC=5(cm)
c) Sai
Áp dụng tính chất đường phân giác trong tam giác ABC, ta có:
BDAB=CDACBDAB=BC−BDACBD6=10−BD88BD=6(10−BD)8BD=60−6BD14BD=60BD=6014≈4,3(cm)
d) Đúng
Theo tính chất đường phân giác trong tam giác ABC, ta có: BDAB=CDAC
Kết hợp với AB=2AM,AC=2AN (vì M, N là trung điểm của AB, AC), ta được:
BD2AM=CD2AN, suy ra 2AN.BD=2AM.CD
Do đó AN.BD=AM.CD (chia cả hai vế cho 2).
Đáp án: ĐSSĐ
Hàm số y=f(x) được xác định bởi công thức y=f(x)=3√x+5. Khi đó f(19) là
Đáp án:
Đáp án:
Thay x=19 vào hàm số để tính f(19).
Thay giá trị x=19 vào công thức hàm số y=f(x)=3√x+5 ta được:
f(19)=3√19+5=3√(13)2+5=3⋅|13|+5=3−13+5=6
Vậy f(19)=6.
Biết khi x=3 thì hàm số y=2x+b có giá trị bằng 4. Giá trị của b là
Đáp án:
Đáp án:
Thay x=3 và y=4 vào hàm số y=2x+b để tính b.
Thay x=3 và y=4 vào hàm số y=2x+b, ta được: 4=2.3+b
Suy ra b=4−2.3=4−6=−2.
Đáp án: -2
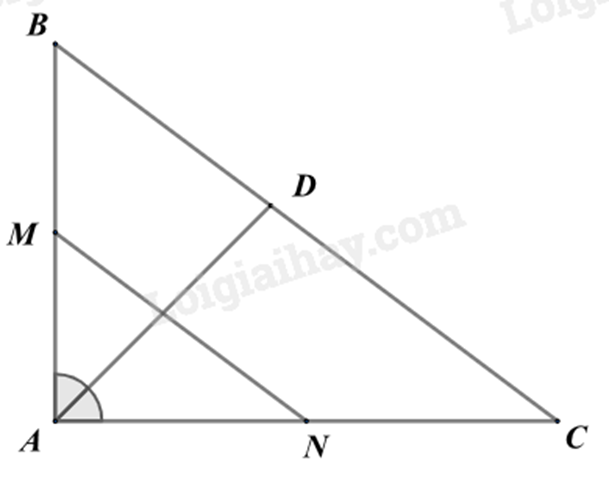
Cho tam giác ABC, đường trung tuyến AD. Gọi M là một điểm trên cạnh AC sao cho AM=12MC. Gọi O là giao điểm của BM và AD. BM bằng bao nhiêu lần OM.
Đáp án:
Đáp án:
Qua D vẽ một đường thẳng song song với BM cắt AC tại N.
Dựa vào định lí đường trung bình của tam giác để chứng minh MN=NC=12MC, AM=MN=12MC.
Từ đó chứng minh OM là đường trung bình của tam giác ΔAND nên OM=12DN.
DN là đường trung bình của ΔMBC nên DN=12BM.
Kết hợp lại để tính được BM bằng bao nhiêu lần OM.
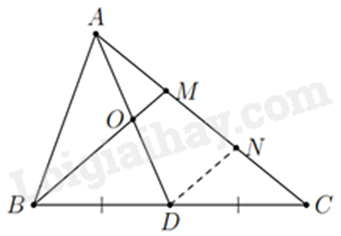
Qua D vẽ một đường thẳng song song với BM cắt AC tại N.
Xét ΔMBC có DB=DC và DN∥BM nên MN=NC=12MC (định lí đường trung bình của tam giác).
Mặt khác AM=12MC (gt), do đó AM=MN=12MC.
Xét ΔAND có AM=MN và BM∥DN nên OA=OD hay O là trung điểm của AD.
Xét ΔAND có:
M là trung điểm của AN (AM = MN), O là trung điểm của AD
nên OM là đường trung bình nên OM=12DN.(1)
Xét ΔMBC có:
N là trung điểm của CM (CN = MN)
D là trung điểm của BC (gt)
nên DN là đường trung bình nên DN=12BM.(2)
Từ (1) và (2) ta có: OM=12DN=12.(12BM)=14BM nên BM=4OM.
Đáp án: 4
Gọi đồ thị hàm số y=4x+2 là đường thẳng d1. Cho hai đường thẳng d2:y=x−1 và d3:y=(6−2m)x. Tìm m để 3 đường thẳng d1,d2,d3 đồng quy.
Đáp án:
Đáp án:
Tìm toạ độ giao điểm của d1,d2 thẳng theo các bước:
Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2: Thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số ta tìm được tung độ giao điểm.
Để 3 đường thẳng d1,d2,d3 đồng quy thì d3 cũng đi qua giao điểm của d1,d2.
Thay toạ độ giao điểm vào d3 để tìm m.
Xét phương trình hoành độ giao điểm của d1,d2, ta có:
4x+2=x−14x−x=−1−23x=−3x=−1
suy ra y=−1−1=−2.
Do đó toạ độ giao điểm của d1,d2 là M(−1;−2).
Để 3 đường thẳng d1,d2,d3 thì d3 phải đi qua điểm M.
Suy ra
−2=(6−2m).(−1)−2=−6+2m2m=−2+62m=4m=2
Đáp án: 2
a) Vẽ đồ thị hàm số y=−x và y=x+3 trên cùng một mặt phẳng toạ độ.
b) Cho hai hàm số bậc nhất y=(m+5)x−3 và y=2x+1. Với giá trị nào của m thì đồ thị của hai hàm số đã cho là hai đường thẳng cắt nhau.
a) Vẽ đồ thị:
* Trường hợp 1: Xét hàm số y=ax(a≠0,b=0):
Để vẽ đồ thị hàm số này ta có thể xác định điểm A(1;a) rồi vẽ đường thẳng đi qua hai điểm O và A.
* Trường hợp 2 : Xét hàm số y=ax+b(a≠0):
Để vẽ đồ thị hàm số này ta có thể xác định hai điểm B(0;b) và C(−ba;0) rồi vẽ đường thẳng đi qua hai điểm đó.
b) Để hai đường thẳng cắt nhau thì a≠a′.
a) * Vẽ đồ thị hàm số y=−x:
Với x=1 thì y=−1, ta được điểm A(1;−1).
Vậy đồ thị hàm số y=−x là đường thẳng OA.
* Vẽ đồ thị hàm số y=x+3:
Với x = 0 thì y = 3, ta được điểm B(0;3)
Với y = 0 thì x = -3, ta được điểm C(-3;0)
Vậy đồ thị hàm số y=x+3 là đường thẳng BC.
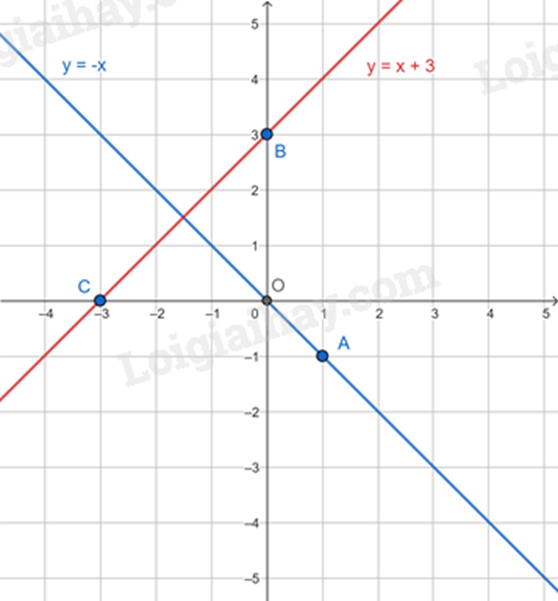
b) Để hai đường thẳng cắt nhau thì a≠a′
hay m+5≠2
m≠2−5
m≠−3
Vậy m≠−3 thì đồ thị của hai hàm số đã cho là hai đường thẳng cắt nhau.
a) Cho tam giác ABC có AB = 6 cm, AC = 8 cm. Đường phân giác của góc A cắt BC tại D. Biết DB = 3 cm. Tính DC.
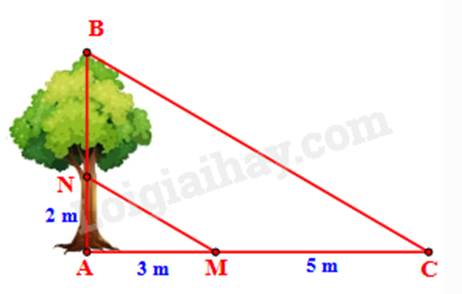
b) Độ cao AN và chiều dài bóng nắng của các đoạn thẳng AN, BN trên mặt đất được ghi lại như trong hình vẽ bên. Tìm chiều cao AB của cây.
a) Sử dụng tính chất của đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.
b) Sử dụng định lí Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
a)
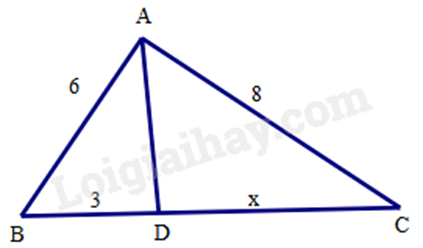
Theo tính chất của đường phân giác, ta có:
ABBD=ACCD63=8xx=8.36=4
b) Vì tia nắng chiếu song song nên MN // BC.
Áp dụng định lí Thalès với MN // BC, ta có:
ANNB=AMMC2NB=35NB=103
Chiều cao AB của cây là: AB=AN+NB=2+103=163(m)
Vậy chiều cao AB của cây là 163m.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365