Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 2 Toán 11 - Chân trời sáng tạo
Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 9
Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 10 Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 8 Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 7 Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 6 Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 5 Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 4 Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 3 Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 2 Đề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 1 Đề cương ôn tập học kì 2 Toán 11 - Chân trời sáng tạoĐề thi học kì 2 Toán 11 Chân trời sáng tạo - Đề số 9
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Rút gọn biểu thức P=x25.6√x với x > 0.
P=√x
P=x1730
P=x115
P=x1715
Đáp án : B
Áp dụng công thức xa.xb=xa+b và b√xa=xab.
P=x25.6√x=x25.x16=x25+16=x1730.
Cho a > 0 và a≠1, khi đó loga3√a bằng
−13
13
−3
3
Đáp án : B
Áp dụng công thức b√xa=xab và logxxα=α.
loga3√a=logaa13=13.
Tập xác định của hàm số y=log5x là
(−∞;+∞)
[0;+∞)
(−∞;0)
(0;+∞)
Đáp án : D
Áp dụng lí thuyết về tập xác định của hàm số logarit.
Tập xác định của hàm số y=log5x là (0;+∞).
Chọn mệnh đề sai.
(u.v)’ = u’.v’
(u – v)’ = u’ – v’
(u.v)’ = u’.v – u.v’
(u + v)’ = u’ + v’
Đáp án : A
Áp dụng công thức tính đạo hàm của tổng, hiệu, tích, thương.
Ta có (u.v)’ = u’.v – u.v’ là công thức đúng và (u.v)’ = u’.v’ là sai.
Hàm số y=x2+x+1 có đạo hàm trên R là
y′=3x
y′=2+x
y′=x2+x
y′=2x+1
Đáp án : D
Áp dụng công thức (xα)′=α.xα−1.
y′=(x2+x+1)′=2x+1.
Đạo hàm của hàm số y=5x là
y′=−5xln5
y′=5xln5
y′=5xln5
y′=−5xln5
Đáp án : C
Áp dụng công thức đạo hàm (ax)′=axlna.
y′=(5x)′=5xln5.
Hệ số góc của tiếp tuyến với đồ thị hàm số y=f(x)=x2 tại điểm có hoành độ x0=−2 là
-4
4
2
-2
Đáp án : B
Tính f’(2).
f′(x)=(x2)′=2x.
Hệ số góc của tiếp tuyến là f’(2) = 2.2 = 4.
Gieo một con xúc xắc cân đối và đồng chất một lần. Gọi A biến cố “Số chấm xuất hiện của con xúc xắc là số chẵn”. Biến cố A xung khắc với biến cố nào sau đây?
“Số chấm xuất hiện của con xúc xắc là số lẻ”
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 3”
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 6”
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 4”
Đáp án : A
Hai biến cố được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra.
Biến cố xung khắc của A là “Số chấm xuất hiện của con xúc xắc là số lẻ”.
Cho A và B là hai biến cố độc lập với nhau. P(A) = 0,4, P(B) = 0,3. Khi đó P(AB) bằng
0,1
0,58
0,7
0,12
Đáp án : D
Áp dụng quy tắc nhân xác suất cho hai biến cố độc lập: P(AB) = P(A).P(B).
Vì A và B là hai biến cố độc lập nên P(AB) = P(A).P(B) = 0,4.0,3 = 0,12.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB vuông góc với mặt phẳng. Khẳng định nào sau đây đúng?
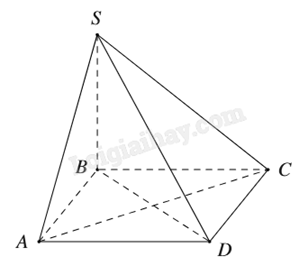
AC⊥(SCD)
AC⊥(SBD)
AC⊥(SBC)
AC⊥(SAB)
Đáp án : B
Đường thẳng vuông góc với mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng.
Vì ABCD là hình vuông nên AC⊥BD.
Mặt khác SB⊥(ABCD) nên SB⊥AC.
Do đó AC⊥(SBD).
Cho hình chóp S.ABC, đáy là tam giác ABC vuông tại B, cạnh SA⊥(ABC). Chọn khẳng định đúng.
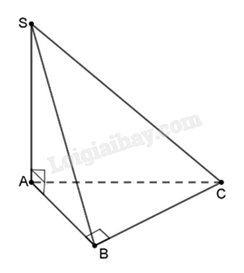
d(C,(SAB))=CS
d(A,(SBC))=AB
d(C,(SAB))=CB
d(S,(SBC))=SA
Đáp án : C
Khoảng cách từ một điểm tới một mặt phẳng là khoảng cách từ điểm đó đến hình chiếu của nó trên mặt phẳng.
Ta có: d(C,(SAB))=CB;
d(A,(SBC)) là khoảng cách từ A đến chân đường vuông góc hạ xuống SB;
d(S,(SBC))=0.
Khối lăng trụ có diện tích đáy bằng a2√3 và chiều cao bằng 2a√3. Thể tích khối lăng trụ đã cho bằng
3a3
2a3
6a3
2a3√3
Đáp án : C
Áp dụng công thức tính thể tích khối lăng trụ V = Bh.
V=Bh=a2√3.2a√3=6a3.
Một chất điểm chuyển động trong 60 giây đầu tiên có phương trình s(t)=112t4−23t3+6t2+7t, trong đó t > 0 và tính bằng giây (s), s(t) tính bằng mét (m).
a) Vận tốc chuyển động v(t)=13t3+2t2+12t+7.
b) Gia tốc chuyển động a(t)=v′(t)=t2−4t+12.
c) Tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất thì vận tốc của vật bằng 773 m/s.
d) Vận tốc chuyển động tại thời điểm t = 1 là v(t)=323 m/s.
a) Vận tốc chuyển động v(t)=13t3+2t2+12t+7.
b) Gia tốc chuyển động a(t)=v′(t)=t2−4t+12.
c) Tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất thì vận tốc của vật bằng 773 m/s.
d) Vận tốc chuyển động tại thời điểm t = 1 là v(t)=323 m/s.
a) v(t) = s’(t).
b) a(t) = v’(t).
c) Tìm t0 sao cho gia tốc nhỏ nhất. Tính v(t0).
d) Tính v(1).
a) Sai. v(t)=s′(t)=13t3−2t2+12t+7.
b) Đúng. a(t)=v′(t)=t2−4t+12.
c) Đúng. Gia tốc của vật đạt giá trị nhỏ nhất tại t=−−42.1=2.
Khi đó v(2)=13.23−2.22+12.2+7=773 (m/s).
d) Sai. v(1)=13.13−2.12+12.1+7=523 (m/s).
Gieo hai đồng xu A và B một cách độc lập. Đồng xu A được chế tạo cân đối. Đồng xu B được chế tạo không cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa.
a) Xác suất đồng xu A xuất hiện mặt ngửa bằng 12.
b) Xác suất đồng xu B xuất hiện mặt ngửa bằng 14.
c) Khi gieo hai đồng xu một lần thì xác suất cả hai đều ngửa bằng 112.
d) Khi gieo hai đồng xu hai lần thì xác suất cả hai đồng xu đều ngửa bằng 132.
a) Xác suất đồng xu A xuất hiện mặt ngửa bằng 12.
b) Xác suất đồng xu B xuất hiện mặt ngửa bằng 14.
c) Khi gieo hai đồng xu một lần thì xác suất cả hai đều ngửa bằng 112.
d) Khi gieo hai đồng xu hai lần thì xác suất cả hai đồng xu đều ngửa bằng 132.
Áp dụng quy tắc nhân xác suất và tính xác suất của biến cố đối.
a) Đúng. Xác suất đồng xu A ngửa bằng 12.
b) Đúng. Xác suất đồng xu B ngửa là x, xác suất đồng xu B sấp là 1 – x.
Vì xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa nên ta có 1−x=3x, suy ra x=14.
Vậy xác suất đồng xu B ngửa bằng 14.
c) Sai. Xác suất cả hai đồng xu đều ngửa là 12.14=18.
d) Sai. Xác suất cả hai đồng xu đều ngửa khi tung hai lần là (12)2.(14)2=164.
Một người lần đầu gửi vào ngân hàng 100 triệu đồng theo thể thức lãi kép (tức là tiền lãi của kỳ trước được cộng vào vốn của kỳ kế tiếp) với kì hạn 3 tháng, lãi suất 2% một quý. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm gửi tiền vào ngân hàng bằng bao nhiêu triệu đồng? Biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay đổi và người đó không rút tiền ra.
Hai đội công nhân trong một nhà máy sản xuất có xác suất tạo ra sản phẩm tốt lần lượt là 0,75 và 0,85. Tính xác suất phế phẩm mà nhà máy đó tạo ra bởi cả hai đội (kết quả làm tròn tới hàng phần trăm).
Cho hàm số f(x)=x2e−2x. Tính tổng các nghiệm của phương trình f′(x)=0.
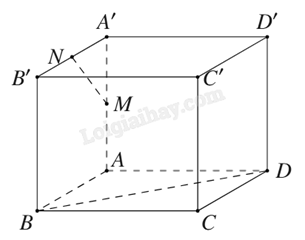
Công ty sản xuất đồ chơi Electric X giao cho nhân viên thiết kế một mô hình khối hình hộp ABCD.A’B’C’ D’ có 6 mặt là hình vuông cạnh bằng 2024 (cm) như hình vẽ. Giả sử M, N lần lượt là trung điểm của cạnh AA′ và A′ B′. Để ghi các thông số kĩ thuật thì công ty yêu cầu nhân viên tính số đo góc giữa hai đường thẳng MN và BD trước khi sản xuất hàng loạt. Hỏi số đo góc giữa hai đường thẳng MN và BD là bao nhiêu độ?
Viết phương trình tiếp tuyến của đồ thị (C): y=x−22x+1 tại giao điểm của (C) với đường thẳng d: y = x – 2.
Lập phương trình hoành độ giao điểm của (C) và d, giải tìm nghiệm x0.
Phương trình tiếp tuyến của f(x) tại x0 là y=f′(x0)(x−x0)+y0.
Ta có: y′=(x−22x+1)′=(x−2)′(2x+1)−(x−2)(2x+1)′(2x+1)2
=1.(2x+1)−(x−2).2(2x+1)2=2x+1−2x+4(2x+1)2=5(2x+1)2.
Phương trình hoành độ giao điểm của d và (C) là x−22x+1=x−2⇔(2x+1)(x−2)=x−2⇔2x2−4x=0⇔2x(x−2)=0
⇔x=0 hoặc x=2.
Với x0=2, ta có y′(x0)=y′(2)=5(2.2+1)2=15; y(x0)=y(2)=2−22.2+1=0.
Phương trình tiếp tuyến là y=15(x−2)+0⇔y=15x−25.
Với x0=0, ta có y′(x0)=y′(0)=5(2.0+1)2=5; y(x0)=y(0)=0−22.0+1=−2.
Phương trình tiếp tuyến là y=5(x−0)−2⇔y=5x−2.
Giải bất phương trình log12[log2(2−x2)]>0.
Tìm ĐKXĐ và giải bất phương trình.
ĐKXĐ: {log2(2−x2)>02−x2>0⇔{2−x2>20x2<2⇔{x2<1x2<2
⇔{−1<x<1−2<x<2⇔−1<x<1.
Khi đó log12[log2(2−x2)]>0⇔log2(2−x2)<(12)0⇔log2(2−x2)<1
⇔2−x2<21⇔x2>0⇔x≠0.
Kết hợp ĐK, ta có tập nghiệm của bất phương trình là S=(−1;0)∪(0;1).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 1, AD = √3, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, khoảng cách giữa AB và SC bằng 32. Tính thể tích V của khối chóp S.ABCD (làm tròn kết quả đến hàng phần trăm).
Xác định đoạn thẳng thể hiện khoảng cách giữa AB và SC. Từ đó, áp dụng hệ thức lượng trong tam giác vuông để tìm chiều cao khối chóp và tính thể tích.
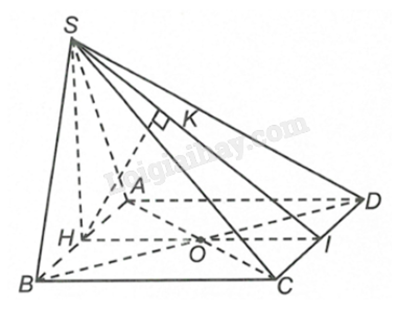
Gọi H, I lần lượt là trung điểm của AB, CD. Kẻ HK⊥SI.
SH vừa là đường cao, vừa là đường trung tuyến của tam giác cân SAB, suy ra SH⊥AB.
Mà (SAB)⊥(ABCD), (SAB)∩(ABCD)=AB nên SH⊥(ABCD)⇒SH⊥CD.
Ta có {SH⊥CDHI⊥CD⇒CD⊥(SHI)⇒CD⊥HK.
Mặt khác {HK⊥SIHK⊥CD⇒HK⊥(SCD).
Vì CD // AB nên d(AB,DC)=d(AB,(SCD))=d(H,(SCD))=HK.
Ta có HK=32, HI=AD=√3.
Xét tam giác vuông SHI vuông tại H có đường cao HK:
1HK2=1HS2+1HI2⇔1HS2=1HK2−1HI2=1(32)2−1(√3)2=19⇔HS=3.
Thể tích khối chóp là VS.ABCD=13.SH.SACBD=13.SH.AB.AD=13.3.1.√3=√3≈1,73.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365