Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 2 Toán 8 - Cánh diều
Đề thi học kì 2 Toán 8 Cánh diều - Đề số 7
Đề thi học kì 2 Toán 8 Cánh diều - Đề số 6 Đề thi học kì 2 Toán 8 - Đề số 5 - Cánh diều Đề thi học kì 2 Toán 8 - Đề số 4 - Cánh diều Đề thi học kì 2 Toán 8 - Đề số 3 - Cánh diều Đề thi học kì 2 Toán 8 - Đề số 2 - Cánh diều Đề thi học kì 2 Toán 8 - Đề số 1 - Cánh diều Đề cương ôn tập học kì 2 Toán 8 - Cánh diềuĐề thi học kì 2 Toán 8 Cánh diều - Đề số 7
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phương trình nào sau đây là phương trình bậc nhất một ẩn?
y2+8x−2022=0y2+8x−2022=0.
3x+6=03x+6=0.
3x−2y−9=03x−2y−9=0.
2x2−4=02x2−4=0.
Đáp án : B
Phương trình bậc nhất một ẩn có dạng ax+b=0(a≠0)ax+b=0(a≠0).
Phương trình bậc nhất một ẩn có dạng ax+b=0(a≠0)ax+b=0(a≠0).
Do đó 3x+6=03x+6=0 là phương trình bậc nhất một ẩn.
Đáp án B
Gọi xx (km) là chiều dài quãng đường AB. Biểu thức biểu thị vận tốc một xe đạp đi từ A đến B trong 5 giờ là
x5x5.
5+x5+x.
5−x5−x.
5x5x.
Đáp án : A
Sử dụng công thức liên hệ giữa vận tốc, thời gian và quãng đường: v=Stv=St.
Biểu thức biểu thị vận tốc của xe đạp đi từ A đến B là: x5x5.
Đáp án A
Một công ty kinh doanh vât liệu xây dựng có bốn kho hàng, mỗi kho hàng có 50 tấn hàng. Biểu đồ cột kép dưới đây biểu diễn số lượng vật liệu đã xuất bán và số lượng vật liệu còn tồn lại trong kho sau tuần lễ kinh doanh đầu tiên.
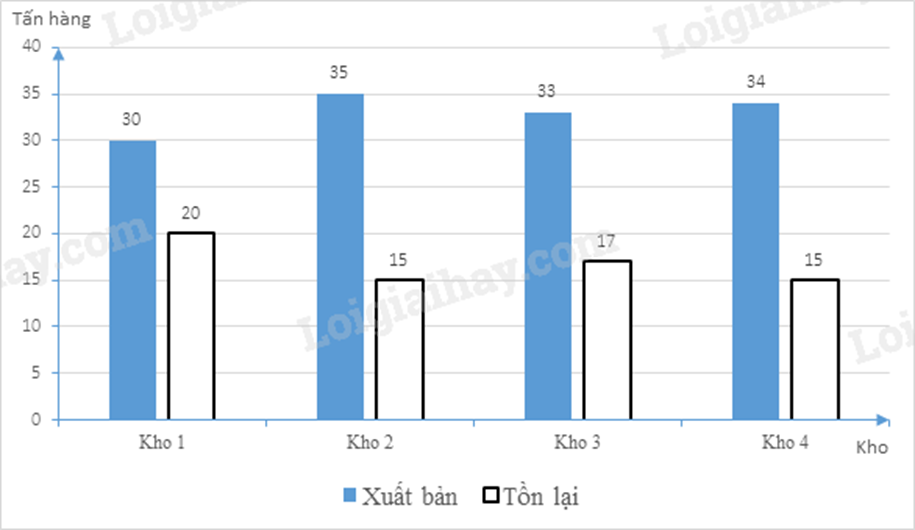
Kế toán đã ghi nhầm số liệu của một kho trong biểu đồ cột kép. Theo em kế toán đã ghi nhầm số liệu ở kho nào?
Kho 1.
Kho 2.
Kho 3.
Kho 4.
Đáp án : D
Mỗi kho hàng có 50 tấn hàng nên lượng Xuất bản và Tồn lại phải có tổng bằng 50.
Kho 1: 30 + 20 = 50 (tấn)
Kho 2: 35 + 15 = 50 (tấn)
Kho 3: 33 + 17 = 50 (tấn)
Kho 4: 34 + 15 = 49 (tấn)
Do đó số tấn hàng của kho 4 chưa chính xác nên kế toán đã ghi nhầm số liệu của kho 4.
Đáp án D
Thống kê tỉ lệ % học sinh lớp 8A chọn môn thể thao yêu thích (mỗi em chọn 1 môn), được cho trong bảng sau:
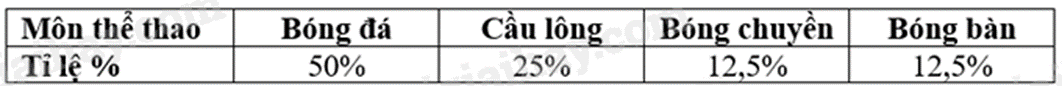
Môn thể thao học sinh lớp 8A8A yêu thích nhiều nhất là
Bóng đá.
Cầu lông.
Bóng chuyền.
Bóng bàn.
Đáp án : A
So sánh tỉ lệ % yêu thích của từng môn thể thao.
Vì 50% > 25% > 12,5% nên môn thể thao học sinh lớp 8A yêu thích nhất là Bóng đá.
Đáp án A
Cho hình vẽ bên, biết BC // ED.
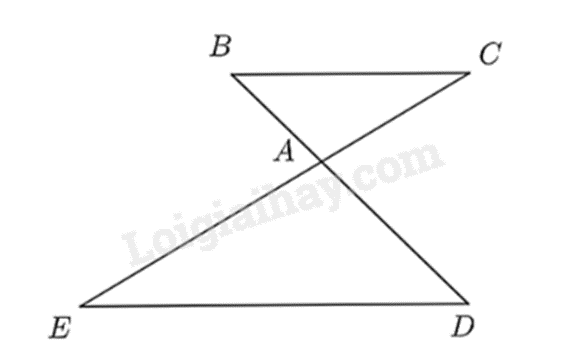
Chọn khẳng định sai trong các khẳng định dưới đây.
ABAD=BCDEABAD=BCDE.
ADAB=AEACADAB=AEAC.
ABDB=ACCE=BCDEABDB=ACCE=BCDE.
ADAB=AEAC=DEBCADAB=AEAC=DEBC.
Đáp án : C
Sử dung định lí Thalès để kiểm tra.
Vì BC // ED nên theo định lí Thalès, ta được:
ADAB=AEAC=DEBCADAB=AEAC=DEBC nên D đúng.
Suy ra ABAD=BCDEABAD=BCDE nên A đúng.
ADAB=AEACADAB=AEAC nên B đúng.
Vậy khẳng định C sai.
Đáp án C
Cho hình vẽ dưới đây.
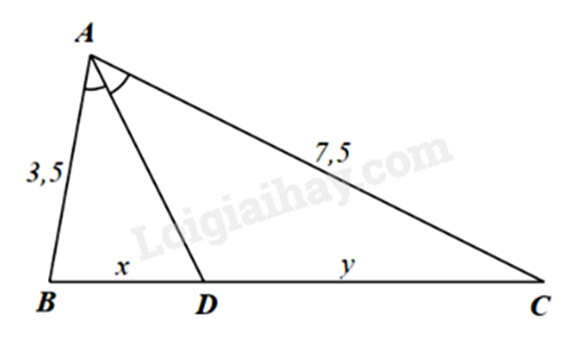
Tỉ số xyxy bằng
715715.
1717.
157157.
115115.
Đáp án : A
Áp dụng tính chất của đường phân giác trong tam giác.
Xét ΔABCΔABC có AD là tia phân giác của ^BACˆBAC nên ta có: xy=DBDC=ABAC=3,57,5=715xy=DBDC=ABAC=3,57,5=715 (tính chất đường phân giác)
Suy ra xy=715xy=715.
Đáp án A
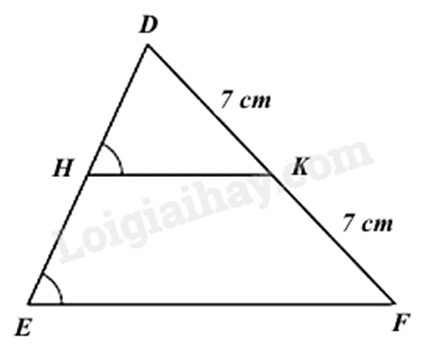
Cho hình vẽ bên. Biết DE = 13 cm, độ dài đoạn thẳng HE là
5,5 cm.
6,5 cm.
7 cm.
8 cm.
Đáp án : B
Chứng minh HK // EF và K là trung điểm của DF nên H là trung điểm của DE và tính được HE.
Vì ^DHK=^DEFˆDHK=ˆDEF, mà hai góc này ở vị trí đồng vị nên HK//EFHK//EF.
Mà DK = KF = 7 cm nên K là trung điểm của DF.
Xét ΔDEFΔDEF có HK//EFHK//EF (cmt) và K là trung điểm của DF nên H là trung điểm của DE.
Do đó HE=12DE=13.13=6,5(cm)HE=12DE=13.13=6,5(cm)
Đáp án B
Cho ΔABCΔABC và ΔDEFΔDEF có ˆA=50∘,ˆB=60∘,ˆD=50∘,ˆE=70∘ˆA=50∘,ˆB=60∘,ˆD=50∘,ˆE=70∘ thì
ΔABC∽ΔDEF.
ΔABC∽ΔDFE.
ΔABC∽ΔEDF.
ΔABC∽ΔFED.
Đáp án : B
Sử dụng định lí tổng ba góc trong tam giác để tính ˆC.
Từ đó chứng minh hai tam giác đồng dạng theo trường hợp góc – góc.
Xét tam giác ABC ta có: ˆA+ˆB+ˆC=180∘ suy ra ˆC=180∘−ˆA−ˆB=180∘−50∘−60∘=70∘.
Xét ΔABC và ΔDEF có:
ˆA=ˆD(=50∘)
ˆC=ˆE(=70∘)
nên ΔABC∽ΔDFE(g.g)
Đáp án B
Cho hình thang vuông ABCD (AB // CD) có đường chéo BD vuông góc với cạnh BC tại B.
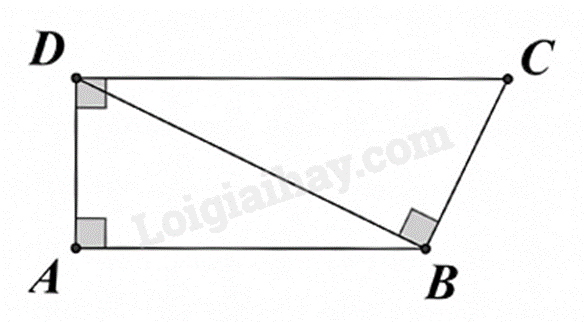
Chọn khẳng định đúng.
ΔDBC∽ΔDAB.
ΔCBD∽ΔDBA.
ΔABD∽ΔBDC.
ΔBAD∽ΔBCD.
Đáp án : C
Từ hai đường thẳng song song suy ra hai góc so le trong bằng nhau.
Chứng minh hai tam giác đồng dạng theo trường hợp góc – góc.
Vì AB // CD nên ^ABD=^BDC (hai góc so le trong)
Xét ΔABD và ΔBDC có:
^DAB=^CBD(=90∘)
^ABD=^BDC (cmt)
Do đó ΔABD∽ΔBDC(g.g)
Đáp án C
Cho hình sau. Biết Hình 1 đồng dạng phối cảnh với Hình 2 với tỉ số đồng dạng là 2. Khi đó tỉ số nào sau đây là đúng?
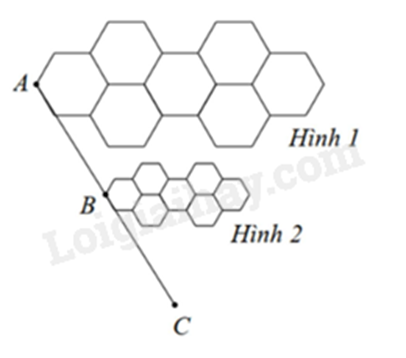
ABBC=2.
ABAC=2.
ACAB=2.
BCAB=2.
Đáp án : C
Sử dụng kiến thức về hình đồng dạng phối cảnh (hình vị tự): Nếu với mỗi điểm M thuộc hình K, lấy điểm M’ thuộc tia OM sao cho OM′=k.OM (hay thì các điểm M’ đó tạo thành hình K′. Hình K′ đồng dạng phối cảnh với hình K theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh và với mỗi điểm M thuộc hình K, lấy điểm M’ thuộc tia OM sao cho OM′OM=k.
Vì Hình 1 đồng dạng phối cảnh với Hình 2 với tỉ số đồng dạng là 2 nên ta có: ACAB=2.
Đáp án C
Chọn ngẫu nhiên một số tự nhiên có một chữ số. Số kết quả có thể xảy ra là:
7.
8.
9.
10.
Đáp án : D
Liệt kê các số tự nhiên có một chữ số, ta được số kết quả có thể xảy ra.
Có 10 số tự nhiên có một chữ số là: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Vậy có 10 kết quả có thể xảy ra.
Đáp án D
Gieo một con xúc xắc cân đối đồng chất. Gọi B là biến cố: “Gieo được mặt có số chấm là số chẵn”. Xác suất của biến cố B là
12.
16.
13.
23.
Đáp án : A
Xác định số kết quả có thể.
Xác định các mặt có số chấm chẵn, ta được số các kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể (tổng số thẻ).
Xúc xắc có 6 mặt: 1; 2; 3; 4; 5; 6 nên có 6 kết quả có thể khi gieo con xúc xắc.
Các mặt có số chấm chẵn là: 2; 4; 6 nên có 3 kết quả thuận lợi cho biến cố B.
Xác suất của biến cố B là 36=12.
Đáp án A
Cho tam giác ABC cân tại A có đường cao AM, N là trung điểm của AC. Kẻ Ax // BC, cắt MN tại E.
a) M là trung điểm của BC.
b) ME // AB.
c) AE = MC.
d) ΔAEN∽ΔCNM.
a) M là trung điểm của BC.
b) ME // AB.
c) AE = MC.
d) ΔAEN∽ΔCNM.
a) Tam giác ABC cân tại A nên đường cao từ đỉnh A đồng thời là đường trung tuyến, suy ra trung điểm của BC.
b) Chứng minh MN là đường trung bình của tam giác ABC để kiểm tra hai đường thẳng song song.
c) Chứng minh AEMB là hình bình hành nên hai cạnh đối bằng nhau.
d) Sử dụng định lí tam giác đồng dạng để chứng minh.
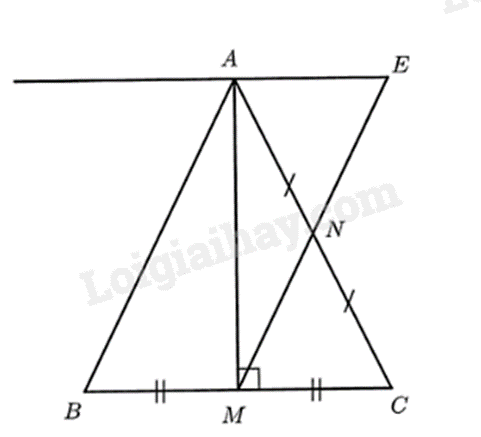
a) Đúng
Vì tam giác ABC cân tại A có AM là đường cao nên AM đồng thời là đường trung tuyến của ΔABC.
Suy ra M là trung điểm của BC.
b) Đúng
Vì M là trung điểm của BC, N là trung điểm của AB nên MN là đường trung bình của tam giác ABC, do đó MN // AB hay ME // AB.
c) Đúng
Ta có: AE // BC và ME // AB nên AEMB là hình bình hành.
Do đó AE = MC.
d) Sai
Ta có: AE // BC nên AE // MC.
Do đó ΔAEN∽ΔCMN (định lí tam giác đồng dạng)
Đáp án: ĐĐĐS
Để chuẩn bị cho buổi thi đua văn nghệ nhân ngày Tết thiếu nhi, cô giáo đã chọn ra 10 học sinh gồm: 4 học sinh nữ là Hoa, Mai, Linh, My; 6 học sinh nam là Cường, Hùng, Nguyên, Kiên, Phúc, Hoàng. Chọn ngẫu nhiên một học sinh trong nhóm các học sinh tập múa trên.
a) Các kết quả có thể xảy ra là 10.
b) Có 6 kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ”.
c) Xác suất của biến cố “Học sinh được chọn là nam” là 0,6.
d) Xác suất của biến cố “Học sinh được chọn là nam và có tên bắt đầu bằng chữ H” là 0,2.
a) Các kết quả có thể xảy ra là 10.
b) Có 6 kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ”.
c) Xác suất của biến cố “Học sinh được chọn là nam” là 0,6.
d) Xác suất của biến cố “Học sinh được chọn là nam và có tên bắt đầu bằng chữ H” là 0,2.
a) Kết quả có thể là tổng số học sinh.
b) Kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ” là số các bạn học sinh nữ.
c) Kết quả thuận lợi cho biến cố “Học sinh được chọn là nam” là số các bạn học sinh nam.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
d) Xác định số kết quả thuận lợi cho biến cố “Học sinh được chọn là nam và có tên bắt đầu bằng chữ H”.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
a) Đúng
Có 10 kết quả có thể xảy ra khi chọn ngẫu nhiên một học sinh trong nhóm tập, đó là: Hoa, Mai, Linh, My, Cường, Hùng, Nguyên, Kiên, Phúc, Hoàng.
b) Sai
Số kết quả thuận lợi cho biến cố “Học sinh được chọn là nữ” là 4 gồm Hoa, Mai, Linh, My.
c) Đúng
Số kết quả thuận lợi cho biến cố “Học sinh được chọn là nam” là 6.
Do đó, xác suất của biến cố “Học sinh được chọn là nam” là: 610=0,6.
d) Sai
Số kết quả thuận lợi cho biến cố “Học sinh được chọn là nam và có tên bằng đầu bằng chữ H” là 2, đó là: Hùng; Hoàng.
Do đó xác suất của biến cố “Học sinh được chọn là nam và có tên bằng đầu bằng chữ H” là: 210=0,2.
Đáp án: ĐSĐS
Số sách quyên góp cho đợt ủng hộ các em nghèo ở vùng cao của khối 8 thuộc một trường trung học cơ sở được ghi lại trong biểu đồ sau:
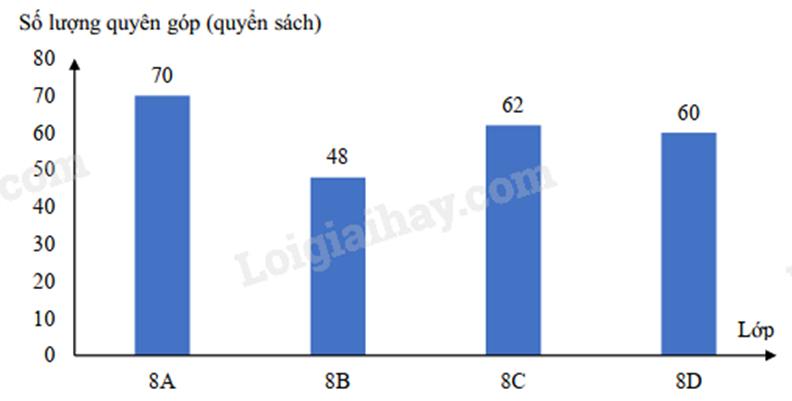
Số sách quyên góp của lớp 8D chiếm bao nhiêu phần trăm so với số sách quyên góp của cả khối? (không cần viết dấu %)
Đáp án:
Đáp án:
Tính tổng số sách khối 8 quyên góp được.
Tính tỉ số phần trăm số sách của lớp 8D với tổng số sách khối 8 quyên góp được.
Số sách khối 8 quyên góp được là:
70+48+62+60=240 (quyển)
Tỉ số phần trăm số sách của lớp 8D với tổng số sách khối 8 quyên góp được là: 70240.100%=25%
Đáp án: 25
Tìm giá trị của x, biết: x3−1+(1−x)(x−5)=0.
Đáp án:
Đáp án:
Sử dụng hằng đẳng thức hiệu hai lập phương rồi đặt nhân tử chung để tìm x.
x3−1+(1−x)(x−5)=0(x−1)(x2+x+1)−(x−1)(x−5)=0(x−1)(x2+x+1−x+5)=0(x−1)(x2+6)=0
Vì x2+6>0 với mọi x nên x−1=0 hay x=1.
Vậy giá trị của x=1.
Đáp án: 1
Để đo chiều cao của một cây xanh một bạn học sinh đã sử dụng một thau nước đặt giữa mình và cây xanh sao cho mắt của bạn học sinh đó khi nhìn vào thau nước thấy được ảnh của ngọn cây trong thau nước, theo như hình vẽ bên dưới:
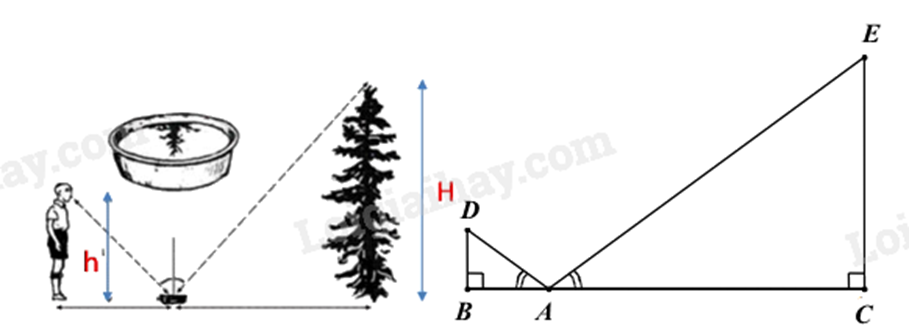
Biết rằng ^BAD=^CAE, khoảng cách từ chân bạn học sinh đến thau nước là đoạn thẳng AB = 2 m; từ thau nước đến gốc cây là đoạn thẳng AC = 7 m, khoảng cách giữa chân bạn học sinh và mắt của mình là đoạn thẳng BD = 1,6 m. Chiều cao EC của cây là bao nhiêu mét?
Đáp án:
Đáp án:
Chứng minh ΔABD∽ΔACE(g.g) suy ra ABAC=BDCE, thay số để tìm CE.
Xét ΔABD và ΔACE có:
^BAD=^CAE(gt)
^ABD=^ACE=90∘
nên ΔABD∽ΔACE(g.g).
Suy ra ABAC=BDCE (tỉ số đồng dạng)
hay 27=1,6CE
suy ra CE=7.1,62=5,6(m)
Vậy cây cao 5,6 m.
Đáp án: 5,6
Một hộp có 50 chiếc thẻ cùng loại, mỗi thẻ ghi một trong các số sau: 1; 2; 3; …; 49; 50, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3”.
(Kết quả ghi dưới dạng số thập phân)
Đáp án:
Đáp án:
Xác định số kết quả có thể.
Xác định các kết quả thuận lợi cho biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3”.
+ Liệt kê các số là bình phương của một số.
+ Xác định các số chia hết cho 3 trong các số đó.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số kết quả có thể.
Các kết quả có thể xảy ra khi rút ngẫu nhiên một thẻ trong hộp là 50.
Kết quả thuận lợi cho biến cố “Thẻ được rút ra là bình phương của một số” là: 1; 4; 9; 16; 25; 36; 49.
Trong các số trên, các số chia hết cho ba là: 9; 36.
Suy ra, có 2 kết quả thuận lợi cho biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3”.
Vậy xác suất của biến cố “Số trên thẻ được rút ra vừa là bình phương của một số, vừa là số chia hết cho 3” là: 250=125=0,04.
Đáp án: 0,04
Một hợp tác xã thu hoạch thóc, dự định thu hoạch 20 tấn thóc mỗi ngày, nhưng khi thu hoạch đã vượt mức 6 tấn mỗi ngày nên không những đã hoàn thành kế hoạch sớm một ngày mà còn thu hoạch vượt mức 10 tấn. Tính số tấn thóc đã dự định thu hoạch.
Gọi số tấn thóc thu hoạch theo dự định là x(tấn) (x>0).
Biểu diễn số ngày thu hoạch hết số thóc theo dự định và số ngày thu hoạch hết số thóc thực tế, từ đó lập phương trình.
Giải phương trình, kiểm tra lại điều kiện và kết luận.
Gọi số tấn thóc thu hoạch theo dự định là x(tấn) (x>0).
Khi đó số ngày thu hoạch hết số thóc theo dự định là: x20 (ngày)
Số tấn thóc thực tế thu hoạch được là: x+10 (tấn)
Số tấn thóc thực tế mỗi ngày thu hoạch được là 20+6=26 (tấn)
Số ngày thu hoạch hết số thóc theo thực tế là: x+1026 ngày
Vì hợp tác xã hoàn thành kế hoạch trước 1 ngày nên ta có phương trình:
x20−1=x+1026
Giải phương trình:
x20−1=x+1026
13x20−260260=10(x+10)26
13x−260260=10x+100260
13x−260=10x+100
13x−10x=100+260
3x=360
x=120 (thỏa mãn)
Vậy số thóc theo dự định là 120 tấn.
Cho hình chữ nhật ABCD. Kẻ AH⊥BD tại H.
a) Chứng minh rằng ΔABD∽ΔHBA.
b) Chứng minh rằng BC2=BD.DH.
c) Kẻ DE là đường phân giác của tam giác ABD. Gọi I là giao điểm của DE và AH. Chứng minh ΔAIE cân và AE2=IH.EB.
a) Chứng minh ^BAD=^AHB=90∘
Từ đó chứng minh ΔABD∽ΔHBA (g.g)
b) Chứng minh ΔABD∽ΔHAD(g.g) suy ra ADDH=BDAD hay AD2=BD.DH
Kết hợp đặc điểm của hình chữ nhật ta có AD = BC
Do đó BC2=BD.DH (đpcm)
c) Chứng minh ΔAIE cân tại A
Sử dụng tính chất tia phân giác cho DE và từ ΔABD∽ΔHAD suy ra ^DBA+^EDB=^HAD+^EDA
Sử dụng tính chất góc ngoài cho ΔAID và ΔDEB để có ^AIE=^HAD+^EDA và ^AEI=^EBD+^BDE
Suy ra ^AIE=^AEI nên ΔAIE cân tại A.
Chứng minh AE2=IH.EB
Từ ΔAIE cân tại A có AE = AI
Kết hợp tính chất đường phân giác DI của tam giác ΔADH suy ra IHIA=DHDA nên IHAE=DHDA
Chứng minh DHAD=ADBD suy ra IHAE=ADBD
Kết hợp tính chất đường phân giác DE của tam giác ΔADB suy ra AEEB=ADBD
Suy ra IHAE=AEEB, do đó AE2=IH.EB.
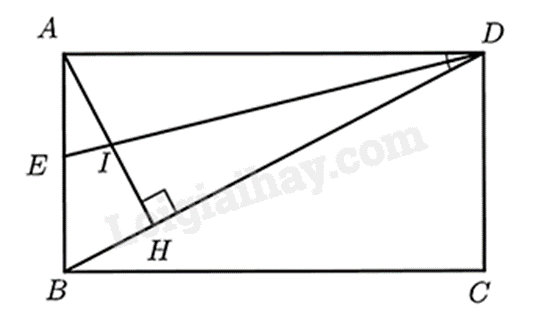
a) Vì ABCD là hình chữ nhật nên ^BAD=90∘.
Vì AH⊥BD tại H nên ta có: ^BAD=^AHB=90∘.
Xét ΔABD và ΔHBA có:
^BAD=^AHB=90∘ (cmt)
^ABD chung
nên ΔABD∽ΔHBA (g.g) (đpcm)
b) Xét ΔABD và ΔHAD có:
^BAD=^AHD=90∘
^BDA chung
nên ΔABD∽ΔHAD(g.g)
suy ra ADDH=BDAD hay AD2=BD.DH
Mà AD = BC (do ABCD là hình chữ nhật)
Do đó BC2=BD.DH (đpcm)
c) Chứng minh ΔAIE cân tại A
Vì DE là đường phân giác của tam giác ABD nên ^ADE=^EDB
Vì ΔABD∽ΔHAD(cmt) nên ^DBA=^HAD (hai góc tương ứng)
suy ra ^DBA+^EDB=^HAD+^EDA (1)
Xét ΔAID có ^AIE=^IAD+^IDA=^HAD+^EDA (tính chất góc ngoài) (2)
Xét ΔDEB có ^AEI=^EBD+^BDE (tính chất góc ngoài) (3)
Từ (1), (2) và (3) suy ra ^AIE=^AEI.
Do đó ΔAIE cân tại A (đpcm)
Chứng minh AE2=IH.EB
ΔAIE cân tại A suy ra AE = AI
Xét ΔADH có DI là đường phân giác nên IHIA=DHDA, suy ra IHAE=DHDA (4)
Vì ΔABD∽ΔHAD(cmt) nên DHAD=ADBD (5)
Từ (4) và (5) suy ra IHAE=ADBD (6)
Xét ΔADB có DE là đường phân giác nên AEEB=ADBD (7)
Từ (6) và (7) suy ra IHAE=AEEB, do đó AE2=IH.EB (đpcm)
Giải phương trình:
1x2+9x+20+1x2+11x+30+1x2+13x+42=118.
Phân tích mẫu thức của cách phân thức ở vế trái thành nhân tử.
Từ đó đưa về dạng 1x(x+1)=1x−1x+1.
Ta có: 1x2+9x+20+1x2+11x+30+1x2+13x+42=118
Phân tích thành nhân tử:
* x2+9x+20=x2+4x+5x+20=(x2+4x)+(5x+20)=x(x+4)+5(x+4)=(x+4)(x+5)
* x2+11x+30=x2+5x+6x+30=(x2+5x)+(6x+30)=x(x+5)+6(x+5)=(x+5)(x+6)
* x2+13x+42=x2+6x+7x+42=(x2+6x)+(7x+42)=x(x+6)+7(x+6)=(x+6)(x+7)
suy ra phương trình trở thành 1(x+4)(x+5)+1(x+5)(x+6)+1(x+6)(x+7)=118
Điều kiện xác định: x≠4;x≠5;x≠6;x≠7
Ta có: 1(x+4)(x+5)+1(x+5)(x+6)+1(x+6)(x+7)=118
1x+4−1x+5+1x+5−1x+6+1x+6−1x+7=1181x+4−1x+7=118x+7−(x+4)(x+4)(x+7)=1183(x+4)(x+7)=118
suy ra (x+4)(x+7)=54
x2+7x+4x+28=54
x2+11x−26=0
x2+13x−2x−26=0
x(x+13)−2(x+13)=0
(x+13)(x−2)=0
Do đó x+13=0 hoặc x−2=0
x=−13 (TM) x=2 (TM)
Vậy nghiệm của phương trình là x=−13;x=2.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365