Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề ôn tập giữa kì 2- Có đáp án và lời giải chi tiết
Đề kiểm tra giữa kì 2 Toán 11 - đề số 4 có lời giải chi tiết
Đề kiểm tra giữa kì 2 Toán 11 - đề số 5 có lời giải chi tiết Đề kiểm tra giữa kì 2 Toán 11 - đề số 3 có lời giải chi tiết Đề kiểm tra giữa kì 2 Toán 11 - đề số 2 có lời giải chi tiết Đề kiểm tra giữa kì 2 Toán 11 - đề số 1 có lời giải chi tiếtĐề kiểm tra giữa kì 2 Toán 11 - đề số 4 có lời giải chi tiết
Đề bài
Câu 1. Tính giới hạn lim5n−3n5n−4.
A. −3 B. 0 C. 5 D. 1
Câu 2. Cho hai đường thẳng a,b phân biệt và mặt phẳng (P). Mệnh đề nào sau đây sai ?
A. Nếu (P)//(Q) và b⊥(P) thì b⊥(Q)
B. Nếu a//(P) và b⊥a thì b⊥(P)
C. Nếu a//(P) và b⊥(P) thì b⊥a
D. Nếu a⊥(P),b⊥(P) thì a//b
Câu 3 . Cho hình chóp S.ABC có SA⊥(ABC); tam giác ABC đều cạnh a và SA=a. Tìm góc giữa SC và mặt phẳng (ABC).
A. 600 B. 900 C. 300 D. 450
Câu 4 . Trong các giới hạn sau giới hạn nào bằng 0 ?
A. limn+3n+2
B. lim(20192020)n
C. lim2n
D. limn4
Câu 5 . Cho tứ diện đều ABCD cạnh a. Tính tích vô hướng →AB.→AC theo a.
A. 12a2 B. a2 C. −a2 D. √32a2
Câu 6 . Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau. Gọi H là trực tâm tam giác ABC. Khẳng định nào sau đây sai.
A. AB⊥OC B. OH⊥(ABC) C. OH⊥BC D. OH⊥OA
Câu 7 . Cho hàm số f(x)=2x+3x−2. Mệnh đề nào sau đây đúng ?
A. Hàm số liên tục trên khoảng (1;5)
B. Hàm số gián đoạn tại x=2020
C. Hàm số liên tục tại x=2
D. Hàm số gián đoạn tại x=2
Câu 8. Trong các giới hạn sau, giới hạn nào có giá trị bằng 5.
A. limx→−2(x2+3x+7)
B. limx→−∞(√x2+10−x)
C. limx→2(3x−2)
D. limx→3−|x−3|
Câu 9 . Trong các mệnh đề sau mệnh đề nào sai
A. limx→13x+22−x=5
B. limx→2+4x+5x−2=+∞
C. limx→+∞(√x2+2x+5−x)=1
D. limx→+∞3x+2x−1=+∞
Câu 10 . Biết ba số x2;8;x theo thứ tự lập thành cấp số nhân. Giá trị của x bằng
A. x=4 B. x=5 C. x=2 D. x=1
Câu 11 . Cho hình lập phương ABCD.A′B′C′D′ . Chọn mệnh đề đúng?
A. →AC=→C′A′
B. →AB+→AD+→AC=→AA′
C. →AB=→CD
D. →AB+→C′D′=→0
Câu 12. Giá trị limx→1x2−3x+2x2−1 bằng:
A. −12 B. 15 C. 13 D. 14
Câu 13 . Cho cấp số cộng (un) có u2=8;u5=17. Công sai d bằng:
A. d=−3 B. d=−5 C. d=3 D. d=5
Câu 14 . Hàm số nào sau đây không liên tục tại x=2.
A. y=√x+2 B. y=sinx
C. y=x2x−2 D. y=x2−3x+2
Câu 15 . Cho cấp số nhân (un) với u1=81 và u2=27. Tìm công bội q?
A. q=−13 B. q=13 C. q=3 D. q=−3
Câu 16 . Cho giới hạn I=limx→+∞4x2+3x+2x2+x−2. Khẳng định nào sau đây đúng
A. I∈(3;5)
B. I∈(2;3)
C. I∈(5;6)
D. I∈(1;2)
Câu 17 . Cho cấp số cộng (un) có u1=19 và d=−2. Tìm số hạng tổng quát un.
A. un=−2n2+33 B. un=−3n+24
C. un=−2n+21 D. un=12+2n
Câu 18 . Giới hạn I=limx→+∞(−2x3+4x+5) bằng
A. I=−∞ B. I=+∞
C. I=−2 D. I=5
Câu 19. Hàm số f(x)=√3+x+√4−x liên tục trên
A. (−3;10) B. [−3;4]
C. [−3;+∞) D. (−∞;4]
Câu 20. Giới hạn J=lim2n+3n+1 bằng:
A. 3 B. 1 C. 2 D. 0
Câu 21. Tính giới hạn J=lim(n−1)(2n+3)n3+2.
A. J=0 B. J=2 C. J=1 D. J=3
Câu 22. Cho tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây sai?
A. AB,CD là hai đường thẳng chéo nhau
B. →AB+→AC+→AD=4→AG
C. →AB,→AC,→AD đồng phẳng
D. →AB+→BC+→CD+→DA=→0
Câu 23. Dãy số nào sau đây không phải là cấp số nhân ?
A. 1;−1;1;−1. B. 1;−3;9;10
C. 1;0;0;0. D. 32;16;8;4
Câu 24. Trong không gian cho ba đường thẳng phân biệt a,b,c.Khẳng định nào sau đây đúng?
A. Nếu avà b cùng nằm trong mặt phẳng (α) mà (α)//a thì a//b.
B. Nếu góc giữa a và c bằng góc giữa b và c thì a//b.
C. Nếu avà b cùng vuông góc với cthì a//b.
D. Nếu a//b và c⊥a thì c⊥b.
Câu 25. Tính giới hạn I=limx→1(x2+3x−5)
A. I=3 B. I=−1 C. I=+∞ D. I=−5
Câu 26. Cho các hàm số y=x2; y=sinx; y=tanx; y=x2−1x2+x+1. Có bao nhiêu hàm số liên tục trên R.
A. 4 B. 3 C. 1 D. 2
Câu 27. Chọn mệnh đề sai
A. lim12n=0
B. lim3n+1=0
C. lim(√n2+2n+3−n)=1
D. lim(−2)n=+∞
Câu 28. Cho hình chóp S.ABC có SA⊥(ABC) và AB⊥BC. Hình chóp S.ABC có bao nhiêu mặt là tam giác vuông?
A. 4 B. 3 C. 2 D. 1
Câu 29. Chọn mệnh đề đúng
A. lim(−2n2+3)=+∞
B. lim√n2+n+1=−∞
C. lim2n+52n+3=1
D. lim2n=0
Câu 30. Cho hình lập phương ABCD.A′B′C′D′. Góc giữa hai đường thẳng AC và DA′ bằng:
A. 300 B. 900 C. 600 D. 00
Câu 31. Cho hình chóp S.ABC có đáy là tam giác đều ABC cạnh bằng a và SC⊥(ABC). Gọi Mlà trung điểm của AB và α là góc tạo bởi đường thẳng SM và mặt phẳng (ABC). Biết SC=a, tính tanα?
A. √217 B. √32
C. 2√77 D. 2√33
Câu 32. Cho hình chóp S.ABCD có đáy là hình vuông ABCD, SA⊥(ABCD) và SA=AB. Gọi E,Flần lượt là trung điểm của BC,SC. Góc giữa EF và mặt phẳng (SAD) bằng:
A. 450 B. 300 C. 600 D. 900
Câu 33. Có bao nhiêu giá trị nguyên của tham số thực m để I<12 biết I=limx→−1(x4−2mx+m2+3)
A. 6 B. 5 C. 8 D. 7
Câu 34. Cho phương trình x3−3x2+3=0. Khẳng định nào sau đây đúng ?
A. Phương trình vô nghiệm
B. Phương trình có đúng 3 nghiệm phân biệt
C. Phương trình có đúng hai nghiệm x=1;x=2.
D. Phương trình có đúng một nghiệm
Câu 35. Cho hình chóp S.ABC có SA=SB=SC. Gọi I là hình chiếu vuông góc của S lên mặt phằng (ABC). Chọn khẳng định đúng trong các khẳng định sau.
A. I là trực tậm của ΔABC
B. I là trung điểm của AB
C. Ilà tâm đường tròn ngoại tiếp của ΔABC
D. I là trọng tâm của ΔABC
Câu 37. Cho cấp số cộng (un) với u1=11;u2=13. Tính tổng S=1u1u2+1u2u3+....+1u99u100.
A. S=9209 B. S=10211
C. S=10209 D. S=9200
Câu 38. Cho cấp số nhân (un) có u2=−2 và u5=54. Tính tổng 1000 số hạng đầu tiên của cấp số nhân đã cho.
A. S1000=31000−12
B. S1000=1−310004
C. S1000=1−310006
D. S1000=31000−16
Câu 39. Cho tứ diện đều ABCD cạnh a. Gọi M là trung điểm của BC. Tính cosin của góc giữa hai đường thẳng AB và DM.
A. √36 B. 12
C. √32 D. √22
Câu 40. Hàm số f(x)=2x+3√x−2 liên tục trên khoảng nào sau đây?
A. (0;4) B. (2;+∞)
C. (0;+∞) D. R
Câu 41. Số điểm gián đoạn của hàm số f(x)=sinxx3+3x2−2x−2?
A. 0 B. 2 C. 1 D. 3
Câu 42. Cho tứ diện ABCD có AC=6a, BD=8a. Gọi M,N lần lượt là trung điểm của AD,BC. Biết AC⊥BD. Tính độ dài đoạn thẳng MN.
A. MN=a√10 B. MN=7a
C. MN=5a D. MN=10a
Câu 43. Cho giới hạn limx→−2(x2−2ax+3+a2)=3 thì a bằng bao nhiêu.
A. a=2 B. a=0 C. a=−2 D. a=−1
Câu 44. Cho hàm số f(x) xác định trên R và thỏa mãn limx→3f(x)=7 thì limx→3[10−2f(x)] bằng bao nhiêu.
A. −4 B. 4 C. 10 D. −14
Câu 45. Gọi S là tập các giá trị của tham số thực m để hàm số f(x)={x2−3xkhix≠1m2+m−8khix=1 liên tục tại x=1. Tích các phần tử của tập S bằng
A. −2 B. −8 C. −6 D. −1
Câu 46. Cho hình vuông ABCD có cạnh bằng a. Người ta dựng hình vuông A1B1C1D1 có cạnh bằng 12 đường chéo của hình vuông ABCD; dựng hình vuông A2B2C2D2 có cạnh bằng 12 đường chéo của hình vuông A1B1C1D1 và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích của tất cả các hình vuông ABCD,A1B1C1D1,A2B2C2D2... bằng 8 thì a bằng:
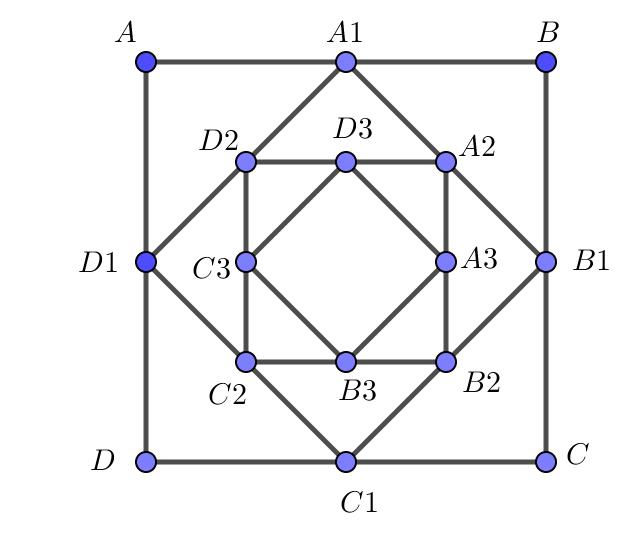
A. 2 B. √2 C. √3 D. 2√2
Câu 47. Cho a,b là các số nguyên và limx→1ax2+bx−5x−1=20. Tính P=a2+b2−a−b.
A. 400 B. 225 C. 325 D. 320
Câu 48. Cho tứ diện ABCD có AB=x(x>0), các cạnh còn lại bằng nhau và bằng 4. Mặt phẳng (P) chứa cạnh AB và vuông góc với cạnh CD tại I. Diện tích tam giác IAB lớn nhất bằng:
A. 12 B. 6 C. 8√3 D. 4√3
Câu 49. Cho hàm số f(x) xác định trên R thỏa mãn limx→2f(x)−16x−2=12. Giới hạn limx→2√2f(x)−16−4x2+x−6 bằng
A. 15 B. 35 C. 20 D. −120
Câu 50. Cho hàm số f(x)={√4x+1−1ax2+(2a+1)xkhix≠03khix=0. Biết a là giá trị để hàm số liên tục tại x0=0, tìm số nghiệm nguyên của bất phương trình x2−x+36a<0.
A. 4 B. 3 C. 2 D. 0
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365