Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1: Một người đi xe máy đoạn đường AB với vận tốc $26\dfrac{1}{4}$ km/h hết $2,4$ giờ. Lúc về, người ấy đi với vận tốc $30$ km/h. Tính thời gian người ấy đi từ B đến A?

     A. $2$ giờ $5$ phút        B. $2$ giờ $6$ phút        C. $2$ giờ                        D. $2$ giờ $4$ phút

Câu 2: Góc bẹt có số đo bằng:

A. ${180^0}$                               B. ${90^0}$                                        C. ${60^0}$                                        D. ${0^0}$

Câu 3: Gieo một con xúc xắc $4$ mặt $50$ lần và quan sát số ghi trên đỉnh của con xúc xắc, ta được kết quả như sau:

Tính xác suất thực nghiệm để gieo được đỉnh có số chẵn:

     A. $\dfrac{9}{{50}}$          B. $\dfrac{{14}}{{50}}$      C. $\dfrac{{15}}{{50}}$      D. $\dfrac{{23}}{{50}}$

Câu 4:

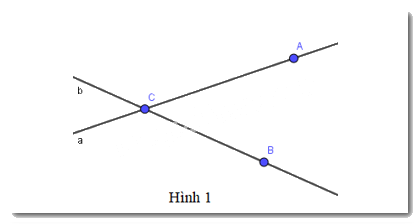
Chọn phát biểu sai trong các phát biểu sau:

     A. Điểm A thuộc đường thẳng a                    

     B.  Hai điểm A, B cùng thuộc đường thẳng a         

     C. Điểm C  thuộc đường thẳng b                                 

     D. Hai điểm B, C cùng thuộc đường thẳng b

Phần II. Tự luận (8 điểm):

Bài 1: (2 điểm) Thực hiện phép tính (tính nhanh nếu có thể):

a) ${\kern 1pt} \dfrac{1}{5} + \dfrac{{ - 5}}{{19}} + \dfrac{4}{5} + \dfrac{{ - 4}}{{19}}$                                                         b) ${\kern 1pt} \dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5}$

c) ${\kern 1pt} 25\% {\rm{\;}} - 1\dfrac{1}{2} + 0,5.\dfrac{3}{8}$                                                     d) ${\kern 1pt} {\left( {\dfrac{{ - 1}}{6}} \right)^2}:\dfrac{5}{{ - 24}} + \left( {\dfrac{7}{{25}} - 36\% } \right).\left| { - 8\dfrac{1}{3}} \right|$

Bài 2: (1,5 điểm) Tìm x, biết:

Tìm $x$, biết: 

a) ${\kern 1pt} x:\dfrac{2}{5} = \dfrac{{ - 15}}{4}$                                               b) ${\kern 1pt} \dfrac{2}{3}.x - \dfrac{1}{2} = 1\dfrac{1}{2}$                                   c) ${\kern 1pt} 0,6.x + 40\% x = 9$

Bài 3: (1,5 điểm) Có một tập bài kiểm tra gồm 45 bài được xếp thành ba loại: Giỏi, khá và trung bình. Trong đó số bài đạt điểm giỏi bằng $\dfrac{1}{3}$ tổng số bài kiểm tra. Số bài đạt điểm khá bằng $90\%$ số bài còn lại.

a) Tính số bài trung bình.

b) Tính tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra.

Bài 4: (2,5 điểm) Cho hai điểm $M,N$ thuộc tia $Ox$ sao cho $OM = 2cm;ON = 5cm$. Điểm $P$ thuộc tia đối của tia $Ox$ sao cho $OP = 3cm$.

a) Điểm $M$ có nằm giữa hai điểm $O$ và $N$ không? Tại sao? Tính $MN.$

b) So sánh$MN$ và $OP.$

c) Gọi $I$ là trung điểm của $OM$. Tính $IO$ và $IP.$

d) Điểm $I$ có là trung điểm của $NP$ không? Tại sao?

Bài 5: (0,5 điểm) Cho biểu thức: $S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}$

Chứng minh $2 < S < 5$

Phần I: Trắc nghiệm

Câu 1

Phương pháp:

Sử dụng công thức: quãng đường = vận tốc . thời gian.

Cách giải:

Độ dài quãng đường AB là: $26\dfrac{1}{4}.2,4\, = \dfrac{{105}}{4}.\dfrac{{25}}{{10}} = 63$ (km)

Thời gian người ấy đi xe máy đi từ B về A là: $63:30 = \dfrac{{21}}{{10}} = 2\dfrac{1}{{10}}$ (giờ) $= 2$ giờ $6$ phút.

Chọn B.

Câu 2

Phương pháp:

Định nghĩa về góc bẹt.

Cách giải:

Góc bẹt có số đo bằng ${180^0}$.

Chọn A.

Câu 3

Phương pháp:

Sử dụng lý thuyết bảng dữ liệu ban đầu.

Cách giải:

Bảng dữ liệu trên điều tra về loài hoa yêu thích của 30 học sinh lớp 6A1.

Chọn B.

Câu 4

Phương pháp:

Quan sát hình vẽ để xác định một điểm thuộc hay không thuộc một đường thẳng.
Cách giải:

Từ hình vẽ ta thấy điểm A, C thuộc đường thẳng a; điểm B, C thuộc đường thẳng b.

Vậy phát biểu sai là hai điểm A, B cùng thuộc đường thẳng a.  

Chọn B.

Phần II: Tự luận

Bài 1

Phương pháp

a) Nhóm các phân số có cùng mẫu số, rồi thực hiện phép tính cộng hai phân số có cùng mẫu số. Muốn cộng hai phân số có cùng mẫu số ta cộng tử với tử và giữ nguyên mẫu.

b) Thực hiện nhóm như sau: $\dfrac{1}{5}.\dfrac{{11}}{{16}} + \dfrac{1}{5}.\dfrac{5}{{16}} + \dfrac{4}{5} = \dfrac{1}{5}.\left( {\dfrac{{11}}{{16}} + \dfrac{5}{{16}}} \right) + \dfrac{4}{5}$ rồi sau đó thực hiện phép tính theo thứ tự ưu tiên. Thực hiện phép tính trong ngoặc trước, ngoài ngoặc sau. Nhân chia trước cộng trừ sau.

c) Viết số phần trăm, hỗn số, số thập phân dưới dạng phân số, rồi thực hiện phép tính theo thứ tự nhân chia trước, cộng trừ sau.

d) Thực hiện phép tính lũy thừa, chuyển số phần trăm , hỗ số về phân số. Thực hiện phép tính theo thứ tự ưu tiên: nhân chia trước, cộng trừ sau. Trong ngoặc trước, ngoài ngoặc sau.

Cách giải:

Bài 2

Phương pháp

a) Muốn tìm số bị chia ta lấy thương nhân với số chia.

b) Chuyển $- \dfrac{1}{2}$ sang vế phải ta đổi dấu thành $+ \dfrac{1}{2}$ ,ta được biểu thức mới có dạng $\dfrac{2}{3}x = 2$ , từ đó tìm được $x$.

c) Viết $40\%$ dưới dạng số thập phân, sử dụng tính chất phân phối của phép nhân đối với phép cộng ta tìm được $x$.

Cách giải:

Bài 3

Phương pháp: Muốn tìm $\dfrac{m}{n}$ của một số $b$ cho trước, ta tính $b.\dfrac{m}{n}\,\left( {m,n \in N,\,n \ne 0} \right)$

Cách giải:

a) Số bài kiểm tra đạt loại giỏi là: $\dfrac{1}{3}.45 = \dfrac{{45}}{3} = 15$ (bài)

Số bài còn lại là: $45 - 15 = 30$ (bài)

Số bài đạt điểm khá là : $90\% .30 = \dfrac{{90}}{{100}}.30 = 27$ (bài)

Số bài đạt điểm trung bình là : $30 - 27 = 3$ (bài)

b) Tỷ số phần trăm số bài đạt điểm trung bình so với tổng số bài kiểm tra là : $\dfrac{3}{{45}} \times 100 \simeq 6.7\%$

Đáp số : a)$3$ bài.      b) $6,7\%$

Bài 4

Phương pháp

Vẽ tia, tia đối, vẽ điểm, trung điểm đoạn thẳng.

Chứng minh một điểm nằm giữa hai điểm còn lại, tính độ dài đoạn thẳng, chứng minh trung điểm.

Cách giải:

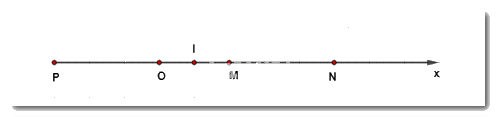
a) Hai điểm M,N cùng thuộc tia $Ox$ và $OM < ON(2cm < 5cm)$ nên điểm $M$ nằm giữa hai điểm $O$ và $N$.

Khi đó $OM + MN = ON$ hay $MN = ON - OM = 5 - 2 = 3cm$.

b) $MN = OP = 3cm$.

c) $I$ là trung điểm của $OM$ nên $IO = IM = \dfrac{{OM}}{2} = 1cm$.

$I$ là trung điểm của $OM$ nên $I$ thuộc tia $Ox$.

$P$ thuộc tia đối của tia $Ox$ nên $O$ nằm giữa $I$ và $P$.

Khi đó ta có $OP + OI = IP$ hay $IP = OP + OI = 3 + 1 = 4cm$.

d) $O$ và $N$ nằm khác phía so với điềm $I$; $O$ và ${\rm{P}}$ nằm cùng phía so với điểm $I$ nên $N$ và $P$ nằm khác phía so với điểm $I$.

Ta tính được $IN = 4cm$.

Do vậy $IP = IN = 4cm$.

Vậy $I$ là trung điểm của đoạn thẳng $NP.$

Bài 5

Phương pháp: Ta chứng minh $S > 2$ và $S < 5$.

Ta thấy :

 $\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right)\\ > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{100.101}}} \right)\end{array}$

Rồi sử dụng : $\dfrac{1}{{n.\left( {n + 1} \right)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}$ để thu gọn S rồi so sánh S với 2.

Tương tự khi so sánh S với 5.

Cách giải:

Ta có:

$\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right) > 5.\left( {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + \dfrac{1}{{4.5}} + ... + \dfrac{1}{{100.101}}} \right) > 5.\left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{100}} - \dfrac{1}{{101}}} \right)\\ > 5.\left( {\dfrac{1}{2} - \dfrac{1}{{101}}} \right) > \dfrac{5}{2} > 2\\ \Rightarrow S > 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\end{array}$

$\begin{array}{l}S = \dfrac{5}{{{2^2}}} + \dfrac{5}{{{3^2}}} + \dfrac{5}{{{4^2}}} + ... + \dfrac{5}{{{{100}^2}}}.\\ = 5.\left( {\dfrac{1}{{2.2}} + \dfrac{1}{{3.3}} + \dfrac{1}{{4.4}} + ... + \dfrac{1}{{100.100}}} \right) < 5.\left( {\dfrac{1}{{1.2}} + \dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{99.100}}} \right)\\ < 5.\left( {1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{{99}} - \dfrac{1}{{100}}} \right) < 5.\left( {1 - \dfrac{1}{{100}}} \right) < 5\\ \Rightarrow S < 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array}$

Từ (1) và (2) : $2 < S < 5$ (đpcm).