Phần trắc nghiệm (3 điểm)

Câu 1: Chọn đáp án đúng

A. $- 7 \in \mathbb{N}$

B. $- 7 \notin \mathbb{Z}$

C. $- 7 \notin \mathbb{Q}$

D. $\frac{1}{2} \in \mathbb{Q}$

Câu 2: Kết quả của phép tính: $\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}$ là

A. $\frac{{ - 1}}{{60}}$

B. $\frac{{ - 17}}{{60}}$

C. $\frac{{ - 5}}{{35}}$

D. $\frac{1}{{60}}$

Câu 3: Kết quả của phép tính: - 0,35. $\frac{2}{7}$ là

A. - 0,1

B. -1

C. -10

D. -100

Câu 4: Kết quả của phép tính: $\frac{{ - 26}}{{15}}:2\frac{3}{5}$ là

A. -6

B. $\frac{{ - 3}}{2}$

C. $\frac{{ - 2}}{3}$

D. $\frac{{ - 3}}{4}$

Câu 5: Kết quả phép tính: $\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}$ là

A. $\frac{{ - 12}}{{20}}$

B. $\frac{3}{5}$

C. $\frac{{ - 3}}{5}$

D. $\frac{{ - 9}}{{84}}$

Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là

A. - 1,8

B. 1,8

C. 0

D. - 2,2

Câu 7: Kết quả phép tính: ${\left( { - \frac{1}{3}} \right)^4}$

A. $\frac{1}{{81}}$.

B. $\frac{4}{{81}}$.

C. $\frac{{ - 1}}{{81}}$.

D. $\frac{{ - 4}}{{81}}$.

Câu 8: Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?

A. 2 hình lập phương, 3 hình hộp chữ nhật;

B. 1 hình lập phương, 3 hình hộp chữ nhật;

C. 2 hình lập phương, 2 hình hộp chữ nhật;

D. 0 hình lập phương, 4 hình hộp chữ nhật.

Câu 9: Hãy chọn khẳng định sai. Hình lập phương ABCD.A'B'C'D' có:

A. 8 đỉnh

B. 4 mặt bên

C. 6 cạnh

D. 6 mặt

Câu 10: Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:

A. HG = 4 cm, HE = 2 cm, GC = 4 cm;

B. HG = 2 cm, HE = 2 cm, GC = 4 cm;

C. HG = 4 cm, HE = 2 cm, GC = 2 cm;

D. HG = 4 cm, HE = 4 cm, GC = 4 cm.

Câu 11: Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.

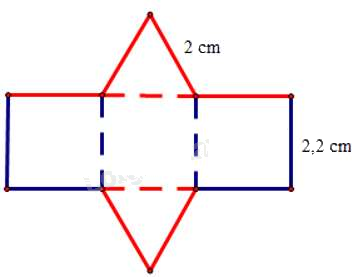
Chiều cao của hình lăng trụ đứng là:

A. 2 cm

B. 2,2 cm

C. 4 cm

D. 4,4 cm

Câu 12: Chọn phát biểu sai:

A. Hai góc đối đỉnh thì bằng nhau;

B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc
đối đỉnh;

C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;

D. Hai góc bằng nhau thì đối đỉnh.

Phần tự luận (7 điểm)

Bài 1: (1 điểm) Tìm x, biết                

a. $x - \frac{3}{4} = \frac{5}{{ - 7}}$

b. 100 - $\left| {x + 1} \right| = 90$

Bài 2. (1,5 điểm) Thực hiện phép tính:

a) $\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}$;

b) $\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}$;

c) $\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}$.

Bài 3. (1 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một
cửa sổ hình vuông với các kích thước như hình vẽ.

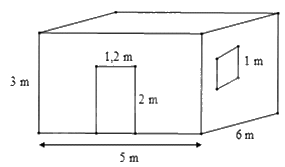
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.

Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước
thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m.
Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).

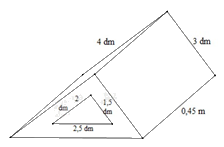
a) Tính thể tích của khối gỗ.
b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).

Bài 5. (1,5 điểm) Cho hình vẽ dưới đây:

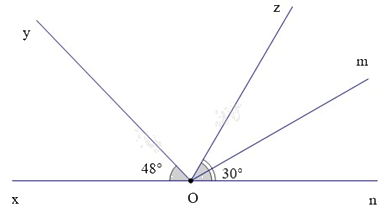
Biết rằng $\widehat {xOy} = {48^0},\widehat {mOn} = {30^0}$ và Om là phân giác của $\widehat {zOn}$.
a) Kể tên các góc (khác góc bẹt) kề với $\widehat {zOm}$; góc kề bù với $\widehat {mOn}$.
b) Tính số đo của góc $\widehat {yOz}$.

Bài 6. (0,5 điểm) Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: ${\rm{M}} = {({\rm{x}} - 5)^2} + 7$

-------- Hết --------

Phần trắc nghiệm (3 điểm)

Câu 1: Chọn đáp án đúng

Phương pháp

Dựa vào các tập hợp số đã học.

Lời giải

Ta có:

$- 7 \notin \mathbb{N}$ nên A sai.

$- 7 \in \mathbb{Z}$ nên B sai.

$- 7 \in \mathbb{Q}$ nên C sai.

$\frac{1}{2} \in \mathbb{Q}$ nên D đúng.

Đáp án D.

Câu 2: Kết quả của phép tính: $\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}}$ là

Phương pháp

Sử dụng quy tắc cộng hai số hữu tỉ.

Lời giải

$\frac{{ - 3}}{{20}} + \frac{{ - 2}}{{15}} = \frac{{ - 9 + \left( { - 8} \right)}}{{60}} = \frac{{ - 17}}{{60}}$

Đáp án B.

Câu 3: Kết quả của phép tính: - 0,35. $\frac{2}{7}$ là

Phương pháp

Sử dụng quy tắc nhân số hữu tỉ.

Lời giải

$- {\rm{ }}0,35.\;\frac{2}{7} =  - \frac{7}{{20}}.\frac{2}{7} =  - \frac{1}{{10}} =  - 0,1$.

Đáp án A.

Câu 4: Kết quả của phép tính: $\frac{{ - 26}}{{15}}:2\frac{3}{5}$ là

Phương pháp

Sử dụng quy tắc chia số hữu tỉ.

Lời giải

$\frac{{ - 26}}{{15}}:2\frac{3}{5} = \frac{{ - 26}}{{15}}:\frac{{13}}{5} = \frac{{ - 26}}{{15}}.\frac{5}{{13}} = \frac{{ - 2}}{3}$

Đáp án C.

Câu 5: Kết quả phép tính: $\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}$ là

Phương pháp

Sử dụng các quy tắc tính với số hữu tỉ.

Lời giải

$\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}} = \frac{3}{4} + \frac{{ - 3}}{{20}} = \frac{3}{5}$.

Đáp án B.

Câu 6: Giá trị của biểu thức : | - 3,4 | : | +1,7 | - 0,2 là

Phương pháp

Xác định giá trị tuyệt đối của -3,4 và +1,7 để tính toán.

Lời giải

| - 3,4 | : | +1,7 | - 0,2 = 3,4 : 1,7 – 0,2 = 2 – 0,2 = 1,8.

Đáp án B.

Câu 7: Kết quả phép tính: ${\left( { - \frac{1}{3}} \right)^4}$

Phương pháp

Dựa vào cách tính lũy thừa của một số.

Lời giải

${\left( { - \frac{1}{3}} \right)^4} = \frac{1}{{81}}$.

Đáp án A.

Câu 8: Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?

A. 2 hình lập phương, 3 hình hộp chữ nhật;
B. 1 hình lập phương, 3 hình hộp chữ nhật;
C. 2 hình lập phương, 2 hình hộp chữ nhật;
D. 0 hình lập phương, 4 hình hộp chữ nhật.

Phương pháp

Quan sát hình vẽ để xác định số hình lập phương và hình hộp chữ nhật.

Lời giải

Quan sát hình trên ta thấy có 1 hình lập phương và 3 hình hộp chữ nhật.

Đáp án B.

Câu 9: Hãy chọn khẳng định sai. Hình lập phương ABCD.A'B'C'D' có:

Phương pháp

Dựa vào kiến thức về hình lập phương.

Lời giải

Hình lập phương có 8 đỉnh nên A đúng.

Hình lập phương có 4 mặt bên và 2 mặt đáy => có tổng 6 mặt nên B và D đúng.

Hình lập phương có 8 cạnh đáy và 4 cạnh bên => có 12 cạnh nên C sai.

Đáp án C.

Câu 10: Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm;
B. HG = 2 cm, HE = 2 cm, GC = 4 cm;
C. HG = 4 cm, HE = 2 cm, GC = 2 cm;
D. HG = 4 cm, HE = 4 cm, GC = 4 cm.        

Phương pháp

Dựa vào tính chất các cạnh của hình hộp chữ nhật.

Lời giải

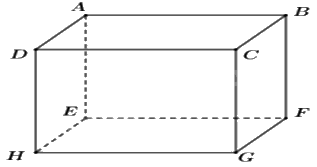
Hình hộp chữ nhật ABCD. EFGH có:

HG = AB = 4cm;

HE = BC = 2cm;

GC = AE = 4cm.

Đáp án A.

Câu 11: Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.

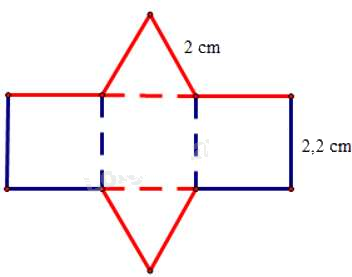
Chiều cao của hình lăng trụ đứng là:

Phương pháp

Quan sát hình vẽ.

Lời giải

Chiều cao của hình lăng trụ đứng là 2,2 cm.

Đáp án B.

Câu 12: Chọn phát biểu sai:
A. Hai góc đối đỉnh thì bằng nhau;
B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc
đối đỉnh;
C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;
D. Hai góc bằng nhau thì đối đỉnh.

Phương pháp

Dựa vào kiến thức về hai góc đối đỉnh.

Lời giải

Hai góc bằng nhau chưa chắc đã là hai góc đối đỉnh nên đáp án D là đáp án sai.

Đáp án D.

Phần tự luận.

Bài 1: (1 điểm). Tìm x, biết               

Phương pháp

Sử dụng quy tắc chuyển vế, kiến thức về giá trị tuyệt đối để giải tìm x.

Lời giải

a. $x - \frac{3}{4} = \frac{5}{{ - 7}}$

$\begin{array}{l}x = \frac{5}{{ - 7}} + \frac{3}{4}\\x = \frac{1}{{28}}\end{array}$

Vậy $x = \frac{1}{{28}}$.

b. 100 - $\left| {x + 1} \right| = 90$

$\begin{array}{l}|x + 1| = 100 - 90\\|x + 1| = 10\end{array}$

=> x + 1 = 10 hoặc x + 1 = -10

hay x = 9 hoặc x = -11.

Vậy x = 9 hoặc x = -11.

Bài 2. (1,5 điểm). Thực hiện phép tính:

Phương pháp

Dựa vào quy tắc tính với số hữu tỉ và lũy thừa để tính.

Lời giải

a) $\frac{2}{3}:\frac{{ - 6}}{9} + \frac{1}{7}$

$= \frac{2}{3}.\frac{{ - 9}}{6} + \frac{1}{7}$$=  - 1 + \frac{1}{7}$$= \frac{{ - 6}}{7}$.

b) $\frac{{ - 3}}{{11}} \cdot \frac{5}{9} + \frac{4}{9} \cdot \frac{{ - 3}}{{11}}$

$= \frac{{ - 3}}{{11}} \cdot \left( {\frac{5}{9} + \frac{4}{9}} \right)$$= \frac{{ - 3}}{{11}}.1$$= \frac{{ - 3}}{{11}}$.

c) $\frac{{{9^5}{{.8}^2}}}{{{{27}^3}.16}}$

$= \frac{{{{\left( {{3^2}} \right)}^5}.{{\left( {{2^3}} \right)}^2}}}{{{{\left( {{3^3}} \right)}^3}{{.2}^4}}}$$= \frac{{{3^{10}}{{.2}^6}}}{{{3^9}{{.2}^4}}}$$= {3.2^2} = 3.4 = 12$

Bài 3. (1 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một
cửa sổ hình vuông với các kích thước như hình vẽ.

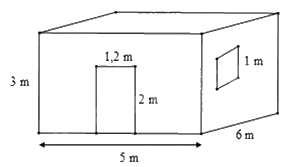
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này
(không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.

Phương pháp

- Tính diện tích phần cần sơn:

Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.

- Tính số tiền bác Long dùng để sơn căn phòng:

Số tiền dùng để sơn = diện tích phần cần sơn . chi phí sơn mỗi mét vuông.

Lời giải

Diện tích xung quanh của căn phòng là: S_xq = 2.(5 + 6).3 = 66(m²).
Diện tích phần cửa lớn và cửa sổ là: 1,2 . 2 + 1 . 1 = 3,4 (m²).
Diện tích phần cần sơn là: 66 – 3,4 = 62,6 (m²)
Tổng chi phí cần để sơn là: 62,6. 30 000 = 1 878 000 (đồng).
Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.

Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước
thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m.
Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là
1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).

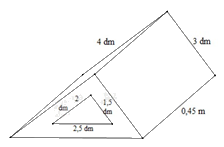
a) Tính thể tích của khối gỗ.
b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).

Phương pháp

a) Sử dụng công thức tính thể tích hình lăng trụ đứng.

b) Tính diện tích xung quanh khối kim loại, diện tích xung quanh lỗ, diện tích đáy.

Diện tích bề mặt cần sơn = diện tích xung quanh của khối gỗ + diện tích xung quanh của cái lỗ - diện tích hai đáy trừ đi diện tích hai cái đáy lỗ.

Lời giải

Đổi: 3 dm = 30 cm; 4 dm = 40 cm; 0,5 m = 50 cm;
1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm; 0,45 m = 45 cm.
a) Thể tích khối gỗ là: $\frac{1}{2}.40.30.45 - \frac{1}{2}.20.15.45{\rm{ }} = {\rm{ }}20250$(cm³)
b) Diện tích xung quanh của gỗ là: (30 + 40 + 50).45 = 5400(cm²)
Diện tích xung quanh của cái lỗ là: (20 +15 + 25).45 = 2700(cm²)
Diện tích hai đáy trừ đi diện tích hai cái đáy lỗ là:

$\frac{1}{2}.30.40 - \frac{1}{2}.15.20 = 450$(cm²)

Diện tích bề mặt cần sơn là: 5400 + 2700 - 450 = 7650(cm²) = 0,765(m²)
Vậy diện tích cần sơn là 0,765m².

Bài 5. (1,5 điểm) Cho hình vẽ dưới đây:

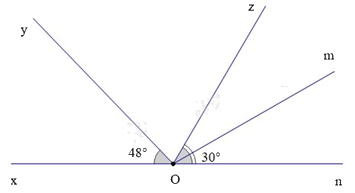
Biết rằng $\widehat {xOy} = {48^0},\widehat {mOn} = {30^0}$ và Om là phân giác của $\widehat {zOn}$.
a) Kể tên các góc (khác góc bẹt) kề với $\widehat {zOm}$; góc kề bù với $\widehat {mOn}$.
b) Tính số đo của góc $\widehat {yOz}$.

Phương pháp

a) Hai góc kề nhau là các góc có một cạnh chung và không có điểm trong chung; hai góc kề bù là hai góc kề nhau và có tổng bằng 180⁰.

b) $\widehat {yOz} = 180 - \widehat {xOy} - \widehat {nOz}$.

Lời giải

a) Các góc (khác góc bẹt) kề với $\widehat {zOm}$ là $\widehat {zOy}$, $\widehat {zOx}$, $\widehat {mOn}$.
Góc kề bù với $\widehat {mOn}$ là $\widehat {mOx}$.

b) Theo bài ta có Om là tia phân giác của $\widehat {zOn}$.

Suy ra $\widehat {zOm} = \widehat {mOn}$ (tính chất tia phân giác của một góc) (1)
Mà $\widehat {zOm} + \widehat {mOn} = \widehat {zOn}$ (hai góc kề nhau) (2)
Từ (1) và (2) suy ra $\widehat {zOm} = \widehat {mOn} = \frac{{\widehat {zOn}}}{2} \Rightarrow \widehat {zOn} = 2\widehat {mOn} = {2.30^0} = {60^0}$
Ta có $\widehat {xOy} + \widehat {yOz} + \widehat {zOn} = \widehat {xOn} = {180^0}$

Hay ${48^0} + \widehat {yOz} + {60^0} = {180^0} \Rightarrow \widehat {yOz} = {180^0} - {48^0} - {60^0} = {72^0}$
Vậy số đo của $\widehat {yOz} = {72^0}$.

Bài 6. (0,5 điểm). Tìm hai số x, y. Tính giá trị nhỏ nhất của biểu thức: ${\rm{M}} = {({\rm{x}} - 5)^2} + 7$

Phương pháp

Dựa vào đặc điểm của biểu thức (x – 5)².

Lời giải

Ta có ${\left( {x - 5} \right)^2} \ge 0,\,\forall x \in \mathbb{R}$ nên ${\left( {x - 5} \right)^2} + 7 \ge 7,\,\forall x \in \mathbb{R}$ hay $M \ge 7$. Dấu “=” xảy ra khi và chỉ khi ${\left( {x - 5} \right)^2} = 0 \Leftrightarrow x = 5$.

Vậy giá trị nhỏ nhất của M là 7 khi x = 5.