Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 1 Toán 8 Cánh diều
Đề thi học kì 1 Toán 8 - Đề số 1 - Cánh diều
Đề thi học kì 1 Toán 8 - Đề số 2 - Cánh diều Đề thi học kì 1 Toán 8 - Đề số 3 - Cánh diều Đề thi học kì 1 Toán 8 - Đề số 4 - Cánh diều Đề thi học kì 1 Toán 8 - Đề số 5 - Cánh diều Đề thi học kì 1 Toán 8 Cánh diều - Đề số 6 Đề thi học kì 1 Toán 8 Cánh diều - Đề số 7 Đề thi học kì 1 Toán 8 Cánh diều - Đề số 8 Đề cương ôn tập học kì 1 Toán 8 - Cánh diềuĐề thi học kì 1 Toán 8 - Đề số 1 - Cánh diều
Phần trắc nghiệm (3 điểm) Câu 1: Thu gọn đa thức 4x2y+6x3y2−10x2y+4x3y24x2y+6x3y2−10x2y+4x3y2 ta được
Thu gọn đa thức 4x2y+6x3y2−10x2y+4x3y24x2y+6x3y2−10x2y+4x3y2 ta được
Đáp án : D
Sử dụng quy tắc tính với đa thức.
Ta có:
4x2y+6x3y2−10x2y+4x3y2=(4x2y−10x2y)+(6x3y2+4x3y2)=−6x2y+10x3y2
Giá trị của đa thức xy+2x2y3−x4y tại x = y = -1 là :
Đáp án : D
Thay x = y = -1 vào đa thức rồi tính toán.
Thay x = y = -1 vào đa thức xy+2x2y3−x4y ta được
(−1).(−1)+2(−1)2.(−1)3−(−1)4(−1)=1−2+1=0
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
1. 14xy5(2x−3y)21x2y(2x−3y)2
2. x2−2x(x−1)2 + 2−xx(x−1)2
3. 25x217y4.34y515x3
4. x2+8x+15x2−9 = …………..x−3
a. 10y3x
b. 2y43x(2x−3y)
c. x + 5
d. 1x−1
1. 14xy5(2x−3y)21x2y(2x−3y)2
b. 2y43x(2x−3y)
2. x2−2x(x−1)2 + 2−xx(x−1)2
d. 1x−1
3. 25x217y4.34y515x3
a. 10y3x
4. x2+8x+15x2−9 = …………..x−3
c. x + 5
Sử dụng các phép tính với phân thức đại số để tìm kết quả đúng.
Đáp án: 1 – b; 2 – d; 3 – a; 4 – c.
Tam giác ABC có đường trung tuyến AM = 2cm; cạnh BC = 4 cm. khi đó:
Đáp án : A
Sử dụng tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông.
Ta có: AM = 2cm; BC = 4cm ⇒AM=12BC. Mà AM là đường trung tuyến ứng với cạnh BC nên AM là đường trung tuyến ứng với cạnh huyền BC hay tam giác ABC vuông tại A.
Một tứ giác có nhiều nhất :
Đáp án : C
Áp dụng định lí tổng các góc của một tứ giác bằng 3600.
- Nếu 4 góc trong tứ giác đều nhọn (nhỏ hơn 900) => Tổng 4 góc < 4.900 = 3600 => Vô lí vì tổng 4 góc trong tứ giác bằng 3600.
- Nếu có 3 góc nhỏ hơn 900 ; 1 góc > 900 => Tổng 3 góc đó < 3.900 = 2700 => góc còn lại lớn hơn 3600−2700=900 (thỏa mãn)
Vậy tứ giác có thể có nhiều nhất 3 góc nhọn.
Hình bình hành là một tứ giác có:
Đáp án : C
Ta sử dụng kiến thức về hình bình hành.
Hình bình hành là một tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên C đúng.
Một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là 6cm và 8cm thì độ dài đường cao ứng với cạnh huyền là:
Đáp án : C
Sử dụng định lí Pythagore và công thức tính diện tích tam giác.
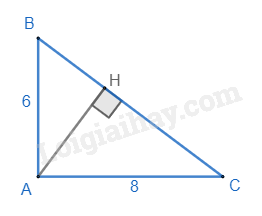
Giả sử tam giác ABC là tam giác vuông có độ dài hai cạnh góc vuông lần lượt là 6cm và 8cm thì độ dài cạnh huyền BC là: BC=√AB2+BC2=√62+82=10 (cm).
Theo công thức tính diện tích tam giác, ta có: SΔABC=12AB.AC=12AH.BC
=> AB.AC = AH.BC
6.8 = AH.10
48 = AH.10
AH = 48:10 = 4,8 (cm).
Cho hình chóp S.ABCD đều có thể tích bằng 100cm3, chiều cao SO bằng 12cm. Độ dài cạnh đáy của hình chóp tứ giác đó là :
Đáp án : B
Dựa vào công thức tính thể tích hình chóp tứ giác để tính độ dài cạnh đáy của hình chóp đó.
V=13Sd.h suy ra Sd=3Vh

Xét hình chóp tứ giác đều S.ABCD có V = 100cm3, đường cao SH = 12cm.
Ta có V=13Sd.h suy ra Sd=3Vh
Sd=3.10012=25.
Vì đáy hình chóp là hình vuông nên độ dài cạnh đáy là √25=5(cm).
Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là:
Đáp án : C
Dựa vào công thức tính diện tích xung quanh của hình chóp tam giác đều
Sxq=pd trong đó p là nửa chu vi đáy, d là trung đoạn.
Nửa chu vi đáy là: p = 5+5+52=7,5 (cm)
Diện tích xung quanh của hình chóp tam giác đều đó là:
Sxq=p.d=7,5.6=45 (cm2).
Cho hàm số y=f(x)=−x2+2. Tính f(−12);f(0) .
Đáp án : B
Thay x=−12 và x = 0 vào hàm số để tính giá trị.
Ta có:
f(−12)=−(−12)2+2=−14+2=74f(0)=−02+2=2
Trong mặt phẳng tọa độ Oxy như hình vẽ, tọa độ điểm Q là :
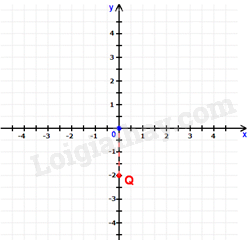
Đáp án : A
Quan sát đồ thị để xác định tọa độ điểm Q.
Điểm Q thuộc trục tung nên có hoành độ bằng 0 và hình chiếu của điểm Q trên trục tung là -2 nên Q(0;−2).
Một cửa hàng gạo nhập vào kho 480 tấn. Mỗi ngày bán đi 20 tấn. Gọi y (tấn) là số gạo còn lại sau x (ngày) bán. Công thức biểu diễn y theo x là :
Đáp án : A
Biểu diễn y theo x.
Số gạo ban đầu là 480 tấn.
Mỗi ngày của hàng bán được 20 tấn thì x ngày cửa hạng bán được 20.x (tấn).
=> Sau x ngày bán, cửa hàng còn lại: 480 – 20x (tấn).
Vậy ta có công thức biểu diễn y theo x là: y = 480 – 20x.
a) Rút gọn biểu thức x2+3xy+2y2x3+2x2y−xy2−2y3 rồi tính giá trị của biểu thức tại x = 5 và y = 3.
b) Phân tích đa thức 2x – 2y – x2 + 2xy – y2 thành nhân tử.
a) Sử dụng các phương pháp phân tích đa thức thành nhân tử để rút gọn biểu thức.
Thay x = 5 và y = 3 vào biểu thức để tính giá trị của biểu thức.
b) Sử dụng các phương pháp phân tích đa thức thành nhân tử.
a) x2+3xy+2y2x3+2x2y−xy2−2y3
=x2+xy+2xy+2y2x3+2x2y−xy2−2y3=x(x+y)+2y(x+y)x2(x+2y)−y2(x−2y)=(x+2y)(x+y)(x2−y2)(x+2y)=x+y(x−y)(x+y)=1x−y
Điều kiện để 1x−y xác định là x−y≠0⇔x≠y.
Tại x = 5 và y = 3 (thỏa mãn điều kiện) thì giá trị của biểu thức 1x−y là: 15−3=12.
Vậy tại x = 5 và y = 3 thì giá trị của biểu thức x2+3xy+2y2x3+2x2y−xy2−2y3 là 12.
b) Phân tích 2x−2y−x2+2xy−y2thành nhân tử, ta được:
2x−2y−x2+2xy−y2=(2x−2y)−(x2−2xy+y2)=2(x−y)−(x−y)2=(x−y)(2−x+y)
Cho biểu thức x2+4x+4x3+2x2−4x−8 (x ≠ ± 2)
a) Rút gọn biểu thức.
b) Tìm x ∈ Z để A là số nguyên.
a) Sử dụng các phương pháp phân tích đa thức thành nhân tử để rút gọn biểu thức.
b) Để A là số nguyên thì mẫu thức phải là ước của tử thức.
a) Ta có:
x2+4x+4x3+2x2−4x−8=(x+2)2x2(x+2)−4(x+2)=(x+2)2(x2−4)(x+2)=x+2(x−2)(x+2)=1x−2
b) Để A là số nguyên thì 1x−2∈Z thì x−2∈ Ư(1) ⇒x−2∈{±1}.
Ta có: x – 2 = 1 ⇒ x = 3 (thỏa mãn điều kiện)
x – 2 = -1 ⇒ x = 1 (thỏa mãn điều kiện)
Vậy A là số nguyên khi x∈{1;3}.
Cho tam giác ABC như hình bên dưới.
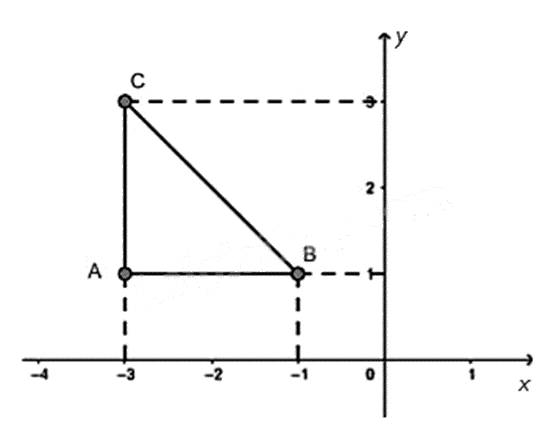
a) Xác định tọa độ các điểm A, B, C.
b) Tam giác ABC có là tam giác vuông cân hay không ?
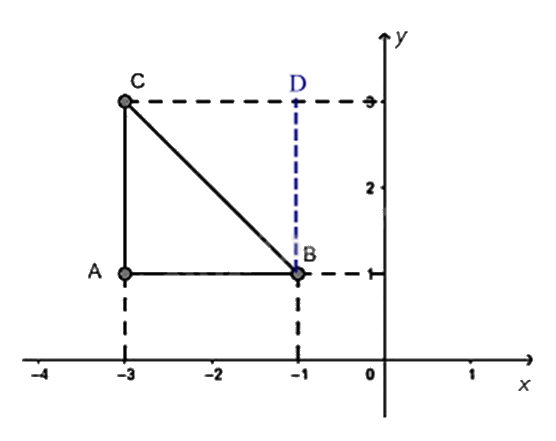
c) Xác định tọa độ điểm D để tứ giác ABDC là hình vuông.
a) Quan sát đồ thị để xác định tọa độ của các điểm.
b) Chứng minh AB ⊥ AC và AB = AC.
c) Để ABDC là hình vuông thì ^ACD=^ABD=900 và AB=BC=CD=DA.
a) Hình chiếu của điểm A trên trục hoành là -3 và trên trục tung là 1. Do đó tọa độ của điểm A là A(−3;1).
Hình chiếu của điểm B trên trục hoành là -1 và trên trục tung là 1. Do đó tọa độ của điểm A là B(−1;1).
Hình chiếu của điểm C trên trục hoành là -3 và trên trục tung là 3. Do đó tọa độ của điểm A là C(−3;3).
Vậy tọa độ của các điểm là: A(−3;1); B(−1;1); C(−3;3).
b) Quan sát hình vẽ, ta thấy
AB//OxAC//OyOx⊥Oy}⇒AB⊥AC⇒ˆA=900
Mà AB = AC (= 2)
⇒ΔABC vuông cân tại A.
c) Ta có: ΔABC vuông cân tại A nên để ABDC là hình vuông thì ^ACD=^ABD=900 và AB = BC = CD = DA hay AC⊥CD;AB⊥BD.
Qua điểm C kẻ đường thẳng vuông góc với Oy.
Qua điểm B kẻ đường thẳng vuông góc với Ox.
Hai đường thẳng này cắt nhau tại điểm D.
CD cắt trục tung tại điểm có tung độ bằng 3.
BD cắt trục hoành tại điểm có hoành độ bằng -1.
=> Tọa độ điểm D là D(−1;3).
Vậy để ABDC là hình vuông thì D(−1;3).
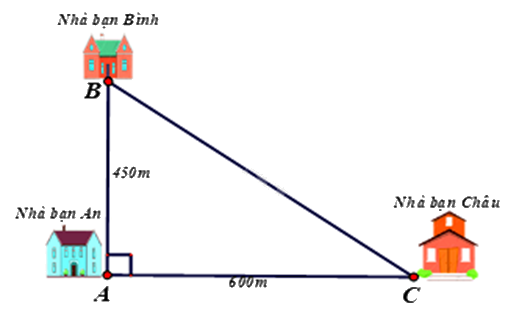
1. Nhà bạn An (vị trí A trên hình vẽ) cách nhà bạn Châu (vị trí C trên hình vẽ) 600m và cách nhà bạn Bình (vị trí B trên hình vẽ) 450m. Biết rằng 3 vị trí: nhà An, nhà Bình và nhà Châu là 3 đỉnh của một tam giác vuông (xem hình vẽ). Hãy tính khoảng cách từ nhà Bình đến nhà Châu.
2. Cho hình thang cân ABCD có DC = 2AB. Gọi M là trung điểm của cạnh DC, N là điểm đối xứng với A qua DC.
a) Chứng minh: Tứ giác ABCM là hình bình hành.
b) Chứng minh: Tứ giác AMND là hình thoi.
c) Khi tứ giác AMND là hình vuông thì góc ABC bằng bao nhiêu?
1. Sử dụng định lí Pythagore.
2.
a) Chứng minh tứ giác ABCM có cặp cạnh song song và bằng nhau.
b) Chứng minh AMND là hình bình hành có một góc vuông.
c) Khi tứ giác AMND là hình vuông suy ra các góc tương ứng để tính số đo góc ABC.
1. Xét tam giác ABC vuông tại A, ta có
BC2 = AB2 + AC2 (Định lí Pythagore)
BC2 = 4502 + 6002
BC2 = 562500
=> BC = 750m
Khoảng cách từ thành phố B đến trạm phát sóng là 750 m
2.

a) Ta có: AB = CM (=12CD) và AB // CM (M ∈ CD) nên ABCM là hình bình hành. (đpcm)
b) Ta có AM = BC (ABCM là hình bình hành)
Mà AD = BC (ABCD là hình thang cân)
=> AM = AD. (1)
Xét tam giác ADH và NDH có:
{AH=NH^AHD=^NHD=900DHchung⇒ΔADH=ΔNDH(c.g.c)
⇒AD=DN (hai cạnh tương ứng). (2)
Tương tự, ta chứng minh được AM = MN. (3)
Từ (1), (2) và (3) suy ra AM = MN = DN = AD => tứ giác AMND là hình thoi. (đpcm)
c) Khi AMND là hình vuông thì ^ADN=900. Trong hình vuông AMND, đường chéo DM là tia phân giác của góc ADN nên ^ADM=^MDN=9002=450.
Góc BAD và góc ADC là hai góc kề một cạnh bên của hình thang ABCD nên ^BAD+^ADC=1800⇒^BAD=1800−450=1350.
Mà ABCD là hình thang cân nên ^BAD=^ABC=1350. (đpcm)
Cho các số x, y thoả mãn đẳng thức 5x2+5y2+8xy−2x+2y+2=0.
Tính giá trị của biểu thức M = (x+y)2017+(x−2)2018+(y+1)2019
Dựa vào hằng đẳng thức a2+2ab+b2=(a+b)2; a2−2ab+b2=(a−b)2 để tìm x, y.
Thay x, y vào biểu thức M để tính giá trị của biểu thức M.
Ta có:
5x2+5y2+8xy−2x+2y+2=0(4x2+8xy+4y2)+(x2−2x+1)+(y2+2y+1)=04(x+y)2+(x−1)2+(y+1)2=0(∗)
Vì 4(x+y)2≥0;(x−1)2≥0;(y+1)2≥0 với mọi x, y
Nên (*) xảy ra khi {x+y=0x−1=0y+1=0⇔{x=−yx=1y=−1⇔{x=1y=−1.
Thay x = 1 và y = -1 vào biểu thức M, ta được:
M=(1−1)2017+(1−2)2018+(−1+1)2019=(−1)2018=1 .
Vậy M = 1 .
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365