Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 1 Toán 8 Cánh diều
Đề thi học kì 1 Toán 8 - Đề số 3 - Cánh diều
Đề thi học kì 1 Toán 8 - Đề số 4 - Cánh diều Đề thi học kì 1 Toán 8 - Đề số 5 - Cánh diều Đề thi học kì 1 Toán 8 Cánh diều - Đề số 6 Đề thi học kì 1 Toán 8 Cánh diều - Đề số 7 Đề thi học kì 1 Toán 8 Cánh diều - Đề số 8 Đề thi học kì 1 Toán 8 - Đề số 2 - Cánh diều Đề thi học kì 1 Toán 8 - Đề số 1 - Cánh diều Đề cương ôn tập học kì 1 Toán 8 - Cánh diềuĐề thi học kì 1 Toán 8 - Đề số 3 - Cánh diều
Phần trắc nghiệm (3 điểm) Câu 1: Kết quả của phép tính (xy + 5)(xy – 1) là:
Kết quả của phép tính (xy + 5)(xy – 1) là:
Đáp án : B
Sử dụng quy tắc nhân hai đa thức.
Ta có:
(xy+5)(xy−1)=x2y2+5xy−xy−5=x2y2+4xy−5
Giá trị của biểu thức 5x2−[4x2−3x(x−2)] tại x = 12 là:
Đáp án : C
Rút gọn biểu thức.
Thay x = 12 vào biểu thức để tính giá trị.
Ta có:
5x2−[4x2−3x(x−2)]=5x2−(4x2−3x2+6x)=5x2−4x2+3x2−6x=4x2−6x
Thay x = 12 vào biểu thức, ta được:4(12)2−6.(12)=1−3=−2.
Rút gọn biểu thức x3−3x2+3x−1x−1 được kết quả nào sau đây?
Đáp án : D
Sử dụng kiến thức về phân thức đại số.
Ta có:
x3−3x2+3x−1x−1=(x−1)3x−1=(x−1)2=x2−2x+1
Hình nào sau đây là hình vuông ?
Đáp án : B
Sử dụng dấu hiệu nhận biết hình vuông.
Hình thang cân có một góc vuông là hình chữ nhật nên A sai.
Hình thoi có một góc vuông là hình vuông nên B đúng.
Tứ giác có 3 góc vuông là hình chữ nhật nên C sai.
Hình bình hành có một góc vuông là hình chữ nhật nên D sai.
AM là trung tuyến của tam giác vuông ABC (ˆA=900;M∈BC) thì:
Đáp án : B
Dựa vào kiến thức về đường trung tuyến ứng với cạnh huyền trong tam giác vuông.
Ta có tam giác ABC vuông tại A và AM là đường trung tuyến (M∈BC) nên AM chính là đường trung tuyến ứng với cạnh huyền của tam giác vuông ABC. Khi đó: AM = 12BC hay BC = 2AM.
Hình bình hành ABCD có ˆA=2ˆB. Số đo góc D là:
Đáp án : A
Dựa vào đặc điểm của hình bình hành.
vuông.
Ta có: ˆA+ˆB=1800 (hai góc kề một cạnh bù nhau). Mà ˆA=2ˆB nên:
2ˆB+ˆB=18003ˆB=1800ˆB=1800:3=600
Có bao nhiêu hình có thể gấp lại (theo các nét đứt) để được hình chóp tứ giác đều?
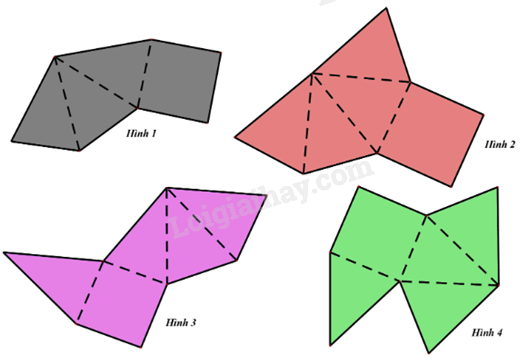
Đáp án : B
Sử dụng kiến thức về hình chóp tứ giác đều.
Hình 2 và hình 3 có thể gấp lại thành hình chóp tứ giác đều.
Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là :
Đáp án : C
Sử dụng công thức tính diện tích xung quanh của hình chóp tam giác đều.
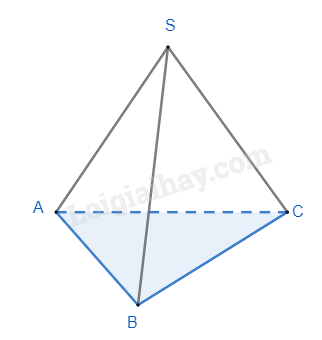
Diện tích xung quanh của hình chóp là:
Sxq=5.32.6=45(cm2)
Hình chóp tứ giác đều S.ABCD có các mặt bên là những tam giác đều AB = 8cm, O là trung điểm của AC. Độ dài đoạn SO là:
Đáp án : C
Sử dụng công thức tính thể tích hình chóp tứ giác đều.
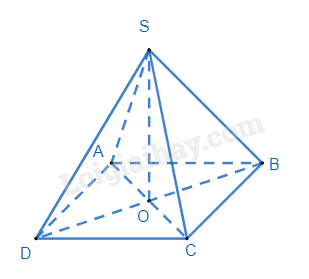
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông, O là trung điểm của AC nên SO là đường cao của hình chóp S.ABCD.
Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore, ta có:
AC2=AB2+BC2=82+82=128⇒AC=√128=8√2⇒AO=8√22=4√2
Vì tam giác SAB đều nên SA = AB = 8cm. Xét tam giác SAO vuông tại O, áp dụng định lí Pythagore, ta có:
SO2=SA2−AO2=82−(4√2)2=32⇒SO=√32
Câu nào sau đây đúng :
Đáp án : D
Sử dụng kiến thức về đồ thị để kiểm tra.
Gốc tọa độ là điểm O(0;0) nên A đúng.
Điểm nằm trên trục hoành có tung độ bằng 0 và điểm nằm trên trục tung có hoành độ bằng 0 nên B, C đúng.
Trong mặt phẳng tọa độ Oxy như hình vẽ, tọa độ điểm A là :
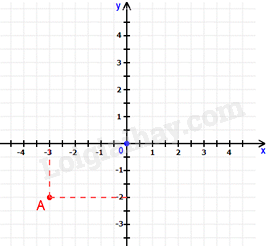
Đáp án : A
Quan sát đồ thị để xác định.
Hình chiếu của điểm A trên trục hoành là -3, trên trục tung là -2 nên tọa độ điểm A là A(-3; -2).
Đồ thị của hàm số y = 13x là đường thẳng OA với O ( 0 ; 0 ) và
Đáp án : C
Thay tọa độ điểm A vào hàm số để xem A có thuộc hàm số hay không.
Với x=1⇒y=13.1=13≠3 nên điểm A(1;3) không thuộc đồ thị hàm số y = 13x.
Với x=−1⇒y=13.(−1)=−13≠−3 nên điểm A(-1;-3) không thuộc đồ thị hàm số y = 13x.
Với x=3⇒y=13.3=1 nên điểm A(3;1) thuộc đồ thị hàm số y = 13x.
Với x=−3⇒y=13.(−3)=−1≠1 nên điểm A(-3;1) không thuộc đồ thị hàm số y = 13x.
Các nhà khoa học đưa ra công thức dự báo nhiệt độ trung bình trên bề mặt Trái Đất như sau: T = 0,02t + 15. Trong đó T là nhiệt độ trung bình của bề mặt Trái Đất tính theo độ C, t là số năm kể từ năm 1950. Nhiệt độ trung bình của bề mặt Trái Đất vào năm 1950 và năm 2022 lần lượt là :
Đáp án : A
Thay t = 1950 – 1950 = 0 và t = 2022 – 1950 = 72 để tính nhiệt độ.
Vào năm 1950, t = 1950 – 1950 = 0 ⇒ T = 0,02.0 + 15 = 15 (0C).
Vào năm 2022, t = 2022 – 1950 = 72 ⇒ T = 0,02.72 + 15 = 16,44 (0C).
Cho phân thức: A=(1x−2+xx+2−x+1x2−4):(1+1x−2)
a) Tìm điều kiện của x để A có nghĩa.
b) Rút gọn A.
c) Tìm các giá trị nguyên của x để A có giá trị nguyên.
a) Để A có nghĩa thì mẫu thức phải khác 0.
b) Sử dụng các phép tính với phân thức để rút gọn.
c) Để A nguyên thì tử thức phải chia hết cho mẫu thức.
a) Điều kiện để A có nghĩa là: {x−2≠0x+2≠0x2−4≠0⇔{x≠2x≠−2
b) Ta có:
A=(1x−2+xx+2−x+1x2−4):(1+1x−2)=[x+2(x−2)(x+2)+x(x−2)(x−2)(x+2)−x+1(x−2)(x+2)]:(x−2+1x−2)=[x+2+x2−2x−x−1(x−2)(x+2)]:(x−1x−2)=x2−2x+1(x−2)(x+2).x−2x−1=(x−1)2(x−2)(x−2)(x+2)(x−1)=x−1x+2
Vậy A=x−1x+2.
c) Ta có: A=x−1x+2=x+2−3x+2=1−3x+2. Để A là số nguyên thì 3x+2 nguyên, hay (x+2)∈U(3)={±1;±3}.
Ta có bảng giá trị sau:
|
x + 2 |
-1 |
1 |
-3 |
3 |
|
x |
-3 (TM) |
-1 (TM) |
-5 (TM) |
1 (TM) |
|
A=x−1x+2 |
4 |
-2 |
2 |
0 |
Vậy để A nguyên thì x∈{−3;−1;−5;1}
Tìm x biết
a) 6x2 – (2x – 3)(3x + 2) = 1
b) (x + 1)3 – (x – 1)(x2 + x + 1) – 2 = 0
Sử dụng các phép tính và hằng đẳng thức đáng nhớ.
a) 6x2 – (2x – 3)(3x + 2) = 1
6x2 – (6x2 – 9x + 4x – 6) = 1
6x2 – 6x2 + 9x – 4x + 6 = 1
5x + 6 = 1
5x = -5
x = -1
Vậy x = -1.2
b) (x + 1)3 – (x – 1)(x2 + x + 1) – 2 = 0
(x3 + 3x2 + 3x + 1) – (x3 – 1) – 2 = 0
x3 + 3x2 + 3x + 1 – x3 + 1 – 2 = 0
3x2 + 3x = 0
3x(x + 1) = 0
[x=0x+1=0[x=0x=−1
Vậy x = 0 hoặc x = -1.
Cho hàm số bậc nhất : y = x + 3 có đồ thị là (d)
a) Vẽ đồ thị (d) của hàm số đã cho.
b) Tìm tọa độ giao điểm của (d) và đường thẳng y = -x + 1.
c) Xác định m để đồ thị hàm số y = (3 - 2m)x + 2 song song với (d).
a) Lấy hai điểm thuộc đồ thị hàm số để vẽ đồ thị,
b) Viết phương trình hoành độ giao điểm của hai đường thẳng để tìm giao điểm.
c) Để hàm số y = (3 - 2m)x + 2 song song với (d) thì 3 – 2m = 1.
a) Cho x = 0 thì y = 0 + 3 = 3. Ta được điểm A(0; 3).
Cho y = 0 thì 0 = x + 3 => x = -3. Ta được điểm B(-3; 0).
Đường thẳng AB chính là đồ thị (d) của hàm số y = x + 3.
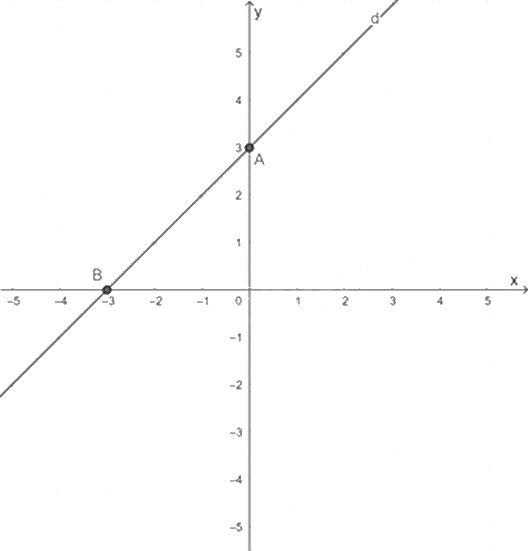
b) Phương trình tọa độ giao điểm của (d) và đường thẳng y = -x + 1 là:
x + 3 = -x + 1 ⇔ 2x = -2 ⇔ x = -1.
Với x = -1 => y = -1 + 3 = 2. Ta được điểm C(-1; 2).
Vậy giao điểm của (d) và đường thẳng y = -x + 1 là C(-1; 2).
c) Để hàm số y = (3 - 2m)x + 2 song song với (d) thì 3 – 2m = 1 hay m = 1. Vậy m = 1 thì hàm số y = (3 - 2m)x + 2 song song với (d).
1. Hình ảnh bên dưới là một thiết kế ngôi nhà hình tam giác cân đang là xu thế mới trên khắp thế giới ở phân khúc nhà nhỏ. Đây là những thiết kế cơ động, có thể thi công lắp dựng nhanh có chi phí rẻ. Trước ngôi nhà có lắp một tấm kính chống vỡ có dạng tam giác cân . Biết cạnh đáy, cạnh bên của miếng kính này lần lượt có độ dài là 8m và 10m. Tính chiều cao của tấm kính tam giác cân này (làm tròn kết quả đến hàng phần mười) ?
2. Cho hình thang ABCD có độ dài đáy lớn bằng 2 lần đáy nhỏ CD . Gọi I là trung điểm của AB. Đường thẳng AD cắt đường thẳng BC tại E .
a) Chứng minh: tứ giác AICD và tứ giác BCDI là hình bình hành.
b) Chứng minh: ^DIA=^ECD và AD = DE.
c) Giả sử ˆA=ˆD=900và AD = CD. Chứng minh BC⊥AC.
1. Dựa vào định lí Pythagore để tính chiều cao của tấm kính.
2.
a) Chứng minh tứ giác AICD; BCDI có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
b) Dựa vào tính chất hai đường thẳng song song để chứng minh ^DIA=^ECD.
Dựa vào tính chất hình bình hành để chứng minh AD = DE.
c) ˆA=ˆD=900 và AD = CD nên hình bình hành AICD trở thành hình vuông. Sử dụng tính chất của hình vuông và hai đường thẳng song song để chứng minh BC⊥AC.
1.
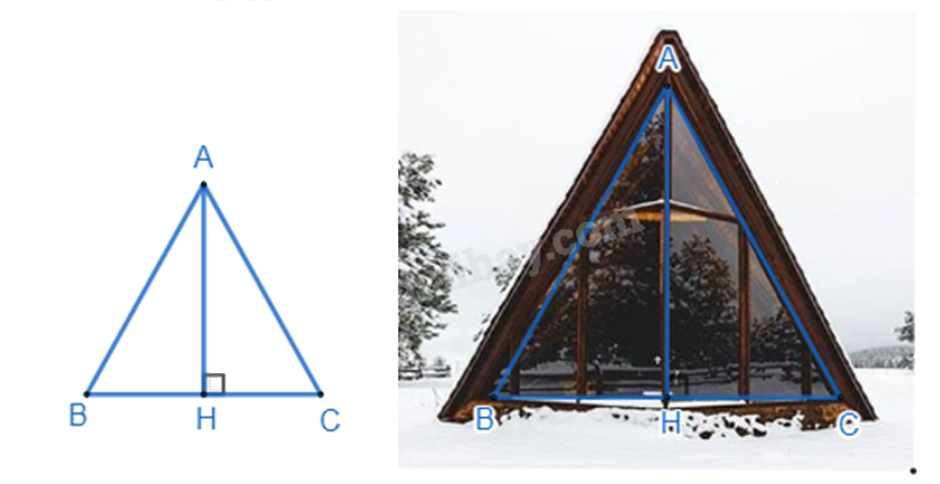
Gọi tam giác ABC là tam giác biểu thị tấm kính tam giác cân.
Kẻ AH⊥BC (H ∈ BC). Vì tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến của tam giác ABC. Khi đó H là trung điểm của BC suy ra BH=12BC=12.8=4(m).
Áp dụng định lí Pythagore vào tam giác vuông AHB, ta có:
AH2=AB2−BH2=102−42=84AH=√84≈9,2(m)
Vậy chiều cao của tấm kính tam giác cân này xấp xỉ 9,2m.
2.
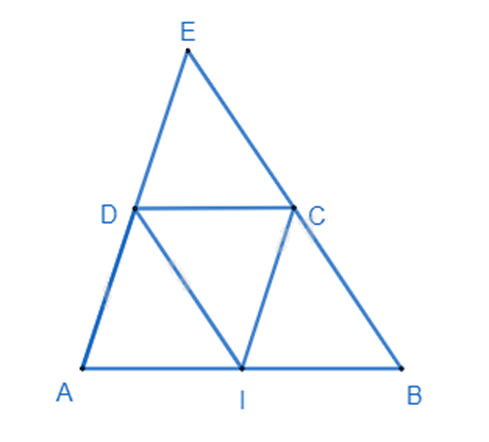
a) Ta có I là trung điểm của AB nên AI=IB=12AB. Mà CD = 12AB suy ra AI = IB = CD.
Xét tứ giác AICD có:
AI // CD (I ∈ AB)
AI = CD (cmt)
=> AICD là hình bình hành. (đpcm)
Xét tứ giác BCDI có:
BI // CD (I ∈ AB)
BI = CD (cmt)
=> BCDI là hình bình hành. (đpcm)
b) BCDI là hình bình hành nên BC // DI => ^DIA=^CBI (hai góc đồng vị).
BI // CD nên ^CBI=^ECD (hai góc đồng vị).
=> ^DIA=^ECD (đpcm).
AICD là hình bình hành nên CI // AD và CI = AD. (1)
Xét tứ giác CEDI có:
CI // DE (CI // AD)
DI // CE (DI // BC)
=> CEDI là hình bình hành => CI = DE (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AD = DE. (đpcm)
c) Vì ˆA=ˆD=900và AD = CD nên hình bình hành AICD trở thành hình vuông. Khi đó AC ⊥ DI.
Mà DI // BC nên AC ⊥ BC. (đpcm)
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365