Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo
Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 9
Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 10 Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 8 Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 7 Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 6 Đề thi giữa kì 2 Toán 7 - Đề số 5 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 7 - Đề số 4 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 7 - Đề số 3 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 7 - Đề số 1 - Chân trời sáng tạoĐề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 9
Phần trắc nghiệm (3 điểm) Câu 1: Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:
Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:
Đáp án : B
Dựa vào kiến thức về tỉ lệ thức.
Ta có: 1,2:1,35=1,21,35=89=8:9.
Biết x2=y3 và x+y=−15. Khi đó giá trị của x, y là
Đáp án : D
Dựa vào tính chất dãy tỉ số bằng nhau.
Ta có: x2=y3=x+y2+3=−155=−3 (tính chất dãy tỉ số bằng nhau)
Suy ra x=−3.2=−6;y=−3.3=−9.
Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:

Giá trị cần điền vào “?” là
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Vì y tỉ lệ thuận với x nên k=yx=−51=−5=1? suy ra ?=1:(−5)=−15.
Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi x=−2 thì y=4. Khi đó, hệ số a bằng bao nhiêu?
Đáp án : C
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
Vì y tỉ lệ nghịch với x theo hệ số tỉ lệ a nên a=xy=(−2).4=−8.
Bộ ba độ dài đoạn thẳng nào sau đây tạo thành một tam giác?
Đáp án : B
Dựa vào quan hệ giữa ba cạnh của một tam giác.
Ta có: 5 – 4 = 1 nên 5cm; 4cm; 1cm không thể tạo thành một tam giác.
3cm; 4cm; 5cm có thể tạo thành một tam giác nên ta chọn đáp án B.
2 + 2 = 4 < 5 nên 5cm; 2cm; 2cm không thể tạo thành một tam giác.
1 + 4 = 5 < 10 nên 1cm; 4cm; 10cm không thể tạo thành một tam giác.
Cho hình vẽ. Hai tam giác trên bằng nhau theo trường hợp
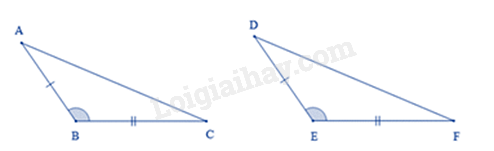
Đáp án : B
Dựa vào kiến thức về hai tam giác bằng nhau.
Xét tam giác ABC và tam giác DEF có:
AB=DE^ABC=^DEFBC=EF
Suy ra ΔABC=ΔDEF (cạnh – góc – cạnh)
Cho hình vẽ. Số đo của ^EFH là
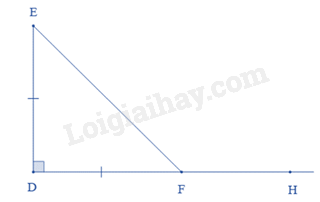
Đáp án : D
Dựa vào tính chất của tam giác cân và hai góc kề bù.
Tam giác DEF có ˆD=900 và DE = DF nên tam giác DEF vuông cân tại D.
Suy ra ^DEF=^DFE=1800−9002=450.
Ta có ^DFE+^EFH=1800 (hai góc kề bù)
Suy ra ^EFH=1800−^DFE=1800−450=1350.
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
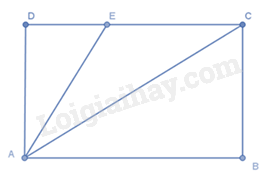
Đáp án : A
Dựa vào quan hệ giữa đường xiên và hình chiếu.
Xét tam giác vuông ACD có AD < AC (trong tam giác vuông, cạnh huyền là cạnh lớn nhất)
Vì E nằm trên cạnh CD nên DE < DC suy ra AE < AC (quan hệ giữa đường vuông góc và đường xiên.
Suy ra AD < AE < AC nên A sai.
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
Đáp án : D
Dựa vào khái niệm về đường trung trực của đoạn thẳng.
“Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó”.
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = –3 thì giá trị của y bằng bao nhiêu?
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.
Vì y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2 nên y=2x.
Thay x=−3 vào công thức ta được: y=2.(−3)=−6.
Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –12 thì y = 8. Khi x = 3 thì y bằng
Đáp án : A
Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.
Vì hai đại lượng x và y là hai đại lượng tỉ lệ nghịch với nhau nên a=−12.8=−96.
Thay x=3 vào công thức ta được: −96=3.y suy ra y=−32.
Hai tam giác bằng nhau là
Đáp án : D
Dựa vào kiến thức về hai tam giác bằng nhau.
Hai tam giác bằng nhau là hai tam giác có ba cặp cạnh, ba cặp góc tương ứng bằng nhau.
Tìm số hữu tỉ x trong các tỉ lệ thức sau:
a) −6x=9−15
b) −4x=x−49
Áp dụng tính chất của tỉ lệ thức.
a) Ta có: −6x=9−15
Suy ra (−6).(−15)=9.x
x=(−6).(−15)9=10
Vậy x = 10.
b) Ta có: −4x=x−49
Suy ra (−4)(−49)=x.x
x2=196x=±14
Vậy x=±14.
a) Cho ab=65. Tìm a, b biết: a – b = 3
b) Cho x2=y3=z5. Tìm x, y, z biết x−y+z=32
Áp dụng tính chất của dãy tỉ số bằng nhau.
a) Ta có: ab=65 suy ra a6=b5.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a6=b5=a−b6−5=31=3.
Suy ra a=3.6=18; b=3.5=15.
Vậy a = 16; b = 15.
b) Ta có: x2=y3=z5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x2=y3=z5=x−y+z2−3+5=324=8.
Suy ra x=8.2=16
y=8.3=24z=8.5=40
Vậy x=16;y=24;z=40.
Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?
Dựa vào tính chất của dãy tỉ số bằng nhau.
Gọi x, y, z (tấn)lần lượt là khối lượng hàng các đơn vị A, B, C vận chuyển (x, y, z > 0).
Theo đề bài ta suy ra: x50=y80=z70 và x+y+z=700
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x50=y80=z70=x+y+z50+80+70=700200=3,5x=175;y=280;z=245
Vậy khối lượng hàng các đơn vị A, B, C vận chuyển lần lượt là 175; 280; 245 tấn.
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
a) Chứng minh OA = OB.
b) Lấy điểm C nằm giữa O và H. Chứng minh ^ACH=^HCB.
c) AC cắt Oy ở D. Trên tia Ox lấy điểm E sao cho OE = OD. Chứng minh ba điểm B, C, E thẳng hàng.
a) Chứng minh được: ∆AHO = ∆BHO (góc – cạnh – góc)
Suy ra OA = OB (hai cạnh tương ứng)
b) Chứng minh được: ∆AHC = ∆BHC (hai cạnh góc vuông)
Suy ra ^ACH=^HCB (hai góc tương ứng)
c) Chứng minh được: ∆OEC = ∆ODC (c.g.c)
Chứng minh được: ^ECO+^OCD+^BCD=1800
Suy ra ba điểm E, C, B thẳng hàng.
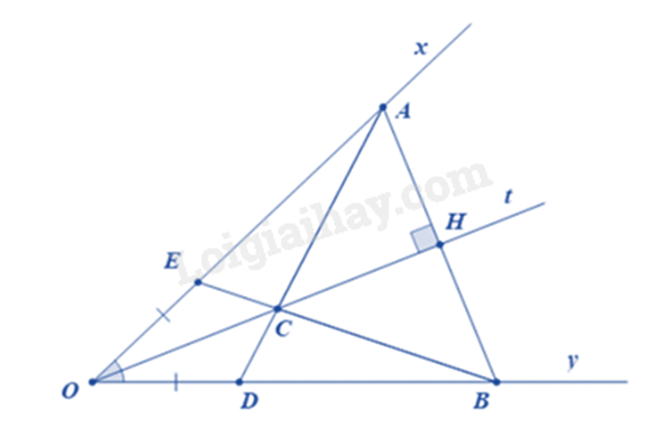
a) Xét tam giác AHO và tam giác BHO có:
^AOH=^BOH (Ot là tia phân giác của ^AOB)
OH chung
^AHO=^BHO(=900)
Suy ra ΔAHO=ΔBHO(g.c.g)
Suy ra OA = OB (hai cạnh tương ứng) (đpcm)
b) ΔAHO=ΔBHO suy ra AH = HB (hai cạnh tương ứng)
Xét tam giác AHC và tam giác BHC có:
HC chung
^AHC=^BHC(=900)
AH = HB
Suy ra ΔAHC=ΔBHC (hai cạnh góc vuông)
Suy ra ^ACH=^HCB (hai góc tương ứng)
c) Xét tam giác OCE và OCD có:
OE = OD
^EOC=^DOC
OC chung
Suy ra ∆OEC = ∆ODC (c.g.c)
Suy ra EC = DC (hai cạnh tương ứng)
Ta có OA = OB và OE = OD nên AE = BD.
Xét ΔECA và ΔDCB có:
EC = ED (cmt)
EA = DB (cmt)
CA = CB (ΔAHC=ΔBHC)
Suy ra ΔECA=ΔDCB (c.c.c)
Suy ra ^ECA=^DCB (hai góc tương ứng)
Mặt khác ^ECA+^ECD=1800 (vì AC cắt Oy tại D)
Suy ra ^DCB+^ECD=1800 hay B, C, E thẳng hàng (đpcm).
Cho tỉ lệ thức ab=cd. Chứng minh: abcd=a2−b2c2−d2.
Đặt ab=cd=k.
Áp dụng dãy tỉ số bằng nhau để chứng minh.
Đặt ab=cd=k⇒{a=bkc=dk
Do đó ta có:
acbd=bkdkbd=k2(1)
Ta cũng có:
a2+c2b2+d2=(bk)2+(dk)2b2+d2=b2k2+d2k2b2+d2=k2(b2+d2)b2+d2=k2(2)
Từ (1) và (2) suy ra:
acbd=a2+c2b2+d2=(k2) (đpcm)
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365