Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 2 Toán 6 Kết nối tri thức
Đề thi học kì 2 Toán 6 - Đề số 11 - Kết nối tri thức
Đề thi học kì 2 Toán 6 - Đề số 12 - Kết nối tri thức Đề thi học kì 2 Toán 6 - Đề số 13 - Kết nối tri thức Đề thi học kì 2 Toán 6 - Đề số 10 Đề thi học kì 2 Toán 6 - Đề số 9 Đề thi học kì 2 Toán 6 - Đề số 8 Đề thi học kì 2 Toán 6 - Đề số 7 Đề thi học kì 2 Toán 6 - Đề số 6 Đề thi học kì 2 Toán 6 - Đề số 5 - Kết nối tri thức Đề thi học kì 2 Toán 6 - Đề số 4 - Kết nối tri thức Đề thi học kì 2 Toán 6 - Đề số 3 - Kết nối tri thức Đề thi học kì 2 Toán 6 - Đề số 2 - Kết nối tri thức Đề thi học kì 2 Toán 6 - Đề số 1 - Kết nối tri thức Đề cương ôn tập học kì 2 Toán 6 - Kết nối tri thứcĐề thi học kì 2 Toán 6 - Đề số 11 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Khoanh tròn vào chữ cái đứng trước câu trả lời đúng: Câu 1: Phân số bằng phân số −25−25 là
Phân số bằng phân số −25−25 là
Đáp án : C
Dựa vào kiến thức về phân số.
−25=−2.35.3=−615−25=−2.35.3=−615.
Đáp án C.
So sánh a=−57a=−57 và b=−87b=−87
Đáp án : A
So sánh 2 phân số có cùng mẫu số dương, phân số nào có tử lớn hơn thì lớn hơn.
Ta có 5<85<8 nên −5>−8−5>−8 suy ra −57>−87−57>−87 hay a > b.
Đáp án A.
Giá trị của xx thoả mãn 6,72−x=6,36,72−x=6,3 là
Đáp án : B
Chuyển vế để tìm x.
6,72−x=6,3x=6,72−6,3x=0,42
Đáp án B.
Số đường thẳng đi qua hai điểm A,B cho trước là:
Đáp án : B
Qua hai điểm bất kỳ chỉ có một đường thẳng đi qua chúng.
Có 1 đường thẳng đi qua hai điểm A, B cho trước.
Đáp án B.
Khẳng định nào sau đây là đúng?
Đáp án : D
Dựa vào kiến thức về trung điểm của đoạn thẳng.
Nếu IA=IB=AB2 thì điểm I là trung điểm của đoạn AB nên D đúng.
Đáp án D.
Trong các dữ liệu sau, dữ liệu nào không phải là số liệu?
Đáp án : C
Dựa vào kiến thức phân loại dữ liệu.
“Tên các loài động vật sống tại vườn quốc gia Cúc Phương” không phải là số liệu.
Đáp án C.
Trong các số sau, số nào là số thập phân âm
Đáp án : B
Số thập phân âm nhỏ hơn 0.
−3,16<0 nên −3,16 là số thập phân âm.
Đáp án B.
Trong các số sau, số nhỏ hơn −12,304 là
Đáp án : A
Dựa vào kiến thức so sánh hai số thập phân.
Ta có: 12,304<12,403 nên −12,304>−12,403.
Đáp án A.
An liệt kê năm sinh của một số thành viên trong gia đình để làm bài tập môn Toán 6, được dãy dữ liệu như sau:

Giá trị không hợp lý trong dãy dữ liệu về năm sinh của các thành viên trong gia đình An là:
Đáp án : A
Quan sát dãy dữ liệu để xác định.
Vì năm hiện tại nhỏ hơn 2050 nên 2050 là giá trị không hợp lý.
Đáp án A.
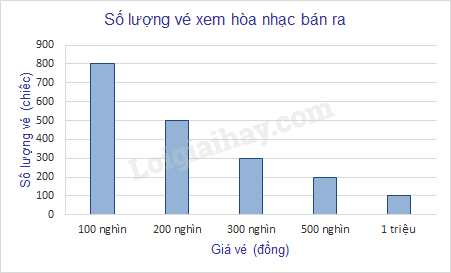
Quan sát biểu đồ sau và cho biết: Có bao nhiêu vé mệnh giá 300 nghìn đồng được bán ra?
Đáp án : A
Quan sát biểu đồ để trả lời.
Số vé mệnh giá 300 nghìn đồng được bán ra là 300 vé.
Đáp án A.
Khẳng định đúng là
Đáp án : D
Dựa vào kiến thức về các loại góc.
Trong các khẳng định trên, chỉ có khẳng định “Góc có số đo 140∘ là góc tù” là khẳng định đúng.
Đáp án D.
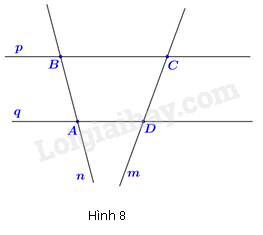
Cho hình vẽ (Hình 8). Khẳng định nào sau đây đúng
Đáp án : C
Quan sát hình vẽ để xác định.
n và q cắt nhau nên A sai.
m và n không song song nên khi kéo dài sẽ có điểm chung nên B sai.
Ba điểm A, B, C không thẳng hàng nên C đúng.
m và p cắt nhau tại C nên D sai.
Đáp án C.
Thực hiện các phép tính (tính hợp lí nếu có thể):
a) −13+76+32.
b) (14−56):52.
c) (−2,25)+7,63.
d) (−8,5).16,35−8,5.83,65.
e) 221.3.322.4.423.5.524.6.
Sử dụng các quy tắc tính với phân số và số thập phân.
a) −13+76+32=−26+76+96=147=73.
b) (14−56):52=(312−1012).25=712.25=76.
c) (−2,25)+7,63=7,63−2,25=5,38.
d) (−8,5).16,35−8,5.83,65=(−8,5).(16,35+83,65)=(−8,5).100=−850.
e) 221.3.322.4.423.5.524.6=2.2.3.3.4.4.5.51.2.3.3.4.4.5.6=26=13.
Bác nông dân có một mảnh vườn hình chữ nhật. Bác dùng 80% diện tích mảnh vườn để trồng cây ăn quả. Biết diện tích trồng cây ăn quả là 460m2. Hỏi diện tích mảnh vườn là bao nhiêu m2?
Biết m% của a là b, ta tính được a = b : m%
Diện tích mảnh vườn là:
460:80%=575(m2).
a) Sắp xếp các phân số theo thứ tự từ bé đến lớn 34;−24;12;−34;74.
b) Tìm phân số nghịch đảo của các phân số sau: 213;1−15.
c) Làm tròn các số sau đến hàng phần trăm: 12,057;40,1534.
a) Đưa các phân số về cùng mẫu dương rồi so sánh tử số với nhau.
b) Hai phân số được gọi là nghịch đảo nếu tích của chúng bằng 0.
c) Sử dụng quy tắc làm tròn số.
a) Ta có: 12=24.
Vì −3<−2<2<3<7 nên −34<−24<24<34<74 hay −34<−24<12<34<74.
b) Các phân số nghịch đảo là: 132;−15.
c) Số 12,057 làm tròn đến hàng phần trăm là 12,06.
Số 40,1534 làm tròn đến hàng phần trăm là 40,15.
a) Cho dãy số liệu về cân nặng (theo đơn vị kilôgam) của 15 học sinh lớp 6 như sau:
40 41 39 45 43 40 41 42 40 39 41 42 45 41 42
Hãy lập bảng thống kê biểu diễn cân nặng của 15 học sinh lớp 6 trên. Dựa vào bảng hãy cho biết có bao nhiêu bạn nặng 45 kilôgam?
b) An gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:

Tính xác suất thực nghiệm của các sự kiện sau:
b1) Số chấm xuất hiện bằng 2;
b2) Số chấm xuất hiện là lớn hơn 3.
a) Đưa các số liệu trên thành bảng thống kê.
Quan sát bảng thống kê để trả lời câu hỏi.
b) Xác suất thực nghiệm của các sự kiện bằng số lần sự kiện đó xảy ra chia cho tổng số lần thực hiện sự kiện.
a) Ta có bảng thống kê:

Quan sát bảng thống kê, ta thấy có 2 bạn nặng 45kg.
b)
b1) Xác suất thực nghiệm của sự kiện số chấm xuất hiện bằng 2 là:
15100=0,15.
b2) Xác suất thực nghiệm của sự kiện số chấm xuất hiện lớn hơn 3 là:
18+10+15100=0,43.
Cho điểm A nằm giữa hai điểm O và B sao cho OA=3cm;OB=6cm.
a) Tính độ dài đoạn thẳngAB?
b) Điểm A có là trung điểm của đoạn thẳng OB không? Vì sao?
a) Tính AB dựa vào OA và OB.
b) Sử dụng tính chất của trung điểm để xác định.
Ta có hình vẽ sau:

a) Vì điểm A nằm giữa O và B nên OA < OB, do đó:
OA + AB = OB
hay 3 + AB = 6
AB = 6 – 3 = 3 (cm)
b) Vì OA = AB = 3cm.
Mà điểm A nằm giữa hai điểm O và B nên A là trung điểm của OB.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365