Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Ôn tập chương I – Căn bậc hai. Căn bậc ba
Lý thuyết Ôn tập chương 1. Căn bậc hai. Căn bậc ba
Trả lời phần câu hỏi ôn tập chương 1: Căn bậc hai, căn bậc ba trang 39 SGK toán 9 tập 1 Bài 70 trang 40 SGK Toán 9 tập 1 Bài 71 trang 40 SGK Toán 9 tập 1 Bài 72 trang 40 SGK Toán 9 tập 1 Bài 73 trang 40 SGK Toán 9 tập 1 Bài 74 trang 40 SGK Toán 9 tập 1 Bài 75 trang 40 SGK Toán 9 tập 1 Bài 76 trang 41 SGK Toán 9 tập 1 Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 1 - Đại số 9 Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 1 - Đại số 9 Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương 1 - Đại số 9 Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 1 - Đại số 9 Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 1 - Đại số 9 Đề kiểm tra 45 phút (1 tiết) - Đề số 6 - Chương 1 - Đại số 9Lý thuyết Ôn tập chương 1. Căn bậc hai. Căn bậc ba
Lý thuyết Ôn tập chương 1. Căn bậc hai. Căn bậc ba
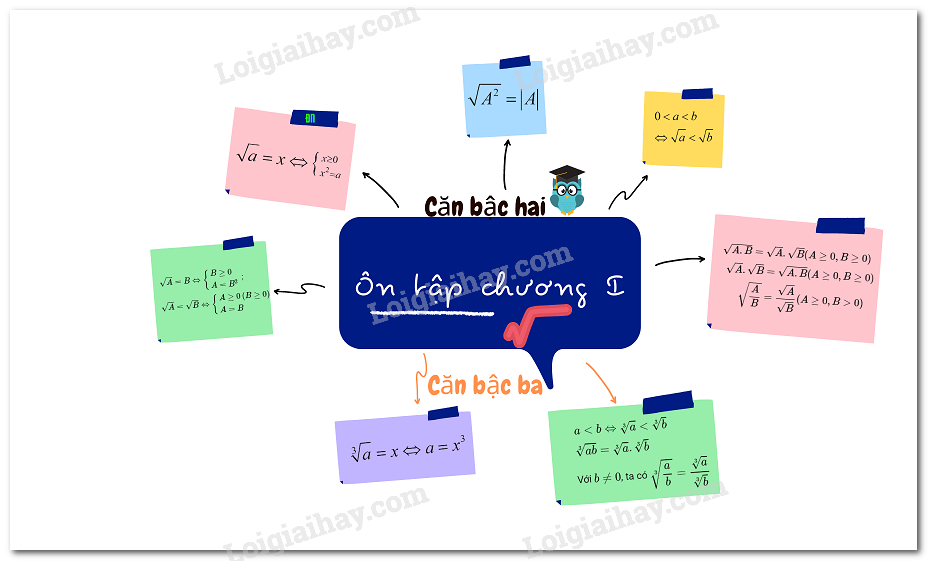
1. Căn bậc hai số học
+) Căn bậc hai của một số không âm là số xx sao cho x2=a.x2=a.
+) Số dương aa có đúng hai căn bậc hai là √a√a (và gọi là căn bậc hai số học của aa) và −√a.−√a.
+) Số 00 có đúng một căn bậc hai là chính số 00 và nó cũng là căn bậc hai số học của 0.0.
+) Với hai số không âm a,b,a,b, ta có a<b⇔√a<√b.a<b⇔√a<√b.
2. Căn thức bậc hai
+) Với AA là một biểu thức đại số, ta gọi √A√A là căn thức bậc hai của AA.
+) √A√A xác định (hay có nghĩa) khi AA lấy giá trị không âm tức là A≥0.A≥0.
√A2=|A|={AkhiA≥0−AkhiA<0.
3. Liên hệ giữa phép nhân, phép chia với phép khai phương
Khai phương một tích: √A.B=√A.√B(A≥0,B≥0)
Nhân các căn bậc hai: √A.√B=√A.B(A≥0,B≥0)
Khai phương một thương: √AB=√A√B(A≥0,B>0)
Chia căn bậc hai: √A√B=√AB(A≥0,B>0)
4. Biến đổi đơn giản biểu thức chứa căn bậc hai
Với A≥0 và B≥0 thì √A2B=A√B
Với A<0 và B≥0 thì √A2B=−A√B
Với A≥0 và B≥0 thì A√B=√A2B
Với A<0 và B≥0 thì A√B=−√A2B
Với A.B≥0 và B≠0 thì √AB=√AB|B|
Với B>0 thì A√B=A√BB
Với A>0 và A≠B2 thì C√A±B=C(√A∓B)A−B2
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365