Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 2 Toán 7 Cánh diều
Đề thi học kì 2 Toán 7 - Đề số 13 - Cánh diều
Đề thi học kì 2 Toán 7 - Đề số 12 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 11 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 10 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 9 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 8 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 7 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 6 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 5 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 4 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 3 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 2 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 1 - Cánh diều Đề cương ôn tập học kì 2 Toán 7 - Cánh diềuĐề thi học kì 2 Toán 7 - Đề số 13 - Cánh diều
Phần trắc nghiệm (3 điểm) Em hãy chọn phương án trả lời đúng Câu 1: Trong các phát biểu sau, dữ liệu nào không phải là số liệu
Trong các phát biểu sau, dữ liệu nào không phải là số liệu
Đáp án : D
Dựa vào kiến thức về phân loại dữ liệu.
Dữ liệu “Các môn học yêu thích của tổ 1” không phải là số liệu.
Đáp án D.
Lượng mưa trung bình của hai tỉnh A (cột trái) và B (cột phải) từ tháng 5 đến tháng 8 được cho bởi biểu đồ:

Lượng mưa trung bình trong 4 tháng ở tỉnh A nhiều hơn tỉnh B bao nhiêu mm?
Đáp án : B
Quan sát biểu đồ để trả lời.
Lượng mưa trung bình của tỉnh A là:
30+32+50+704=45,5(mm)30+32+50+704=45,5(mm)
Lượng mưa trung bình của tỉnh B là:
10+15+50+804=38,75(mm)10+15+50+804=38,75(mm)
Lượng mưa trung bình trong 4 tháng ở tỉnh A nhiều hơn tỉnh B là:
45,5−38,75=6,7545,5−38,75=6,75
Đáp án B.
Có bao nhiêu đơn thức trong các biểu thức sau: 2x2x;8+4x8+4x; 5x65x6; 5xy5xy; 13x−113x−1?
Đáp án : A
Đơn thức là biểu thức đại số có dạng tích của một số thức với một lũy thừa của một biến.
Trong các biểu thức trên, các đơn thức là: 2x2x; 5x65x6; 5xy5xy.
Vậy có 3 đơn thức.
Đáp án A.
Bậc của đa thức 3x3−5x2+17x−293x3−5x2+17x−29 là
Đáp án : D
Bậc của hạng tử có bậc cao nhất là bậc của đa thức.
Bậc của đa thức 3x3−5x2+17x−293x3−5x2+17x−29 là 3 vì 3x33x3 có bậc lớn nhất (bậc là 3)
Đáp án D.
Đa thức nào là đa thức một biến?
Đáp án : B
Đa thức một biến là tổng của những đơn thức của cùng một biến.
Đa thức x3−6x2+9x3−6x2+9 là đa thức một biến với biến là x.
Đáp án B.
Tích của hai đơn thức 7x27x2 và 3x3x là
Đáp án : B
Để nhân hai đơn thức ta nhân hay hệ số với nhau và nhân hai lũy thừa của biến với nhau.
Ta có: 7x2.3x=21x37x2.3x=21x3.
Đáp án B.
Một hộp phấn màu có nhiều màu: màu cam, màu vàng, màu đỏ, màu hồng, màu xanh. Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả?
Đáp án : D
Liệt kê các kết quả có thể xảy ra.
Khi rút bất kì một cây bút màu thì có 5 kết quả có thể xảy ra, đó là: màu cam, màu vàng, màu đỏ, màu hồng, màu xanh.
Đáp án D.
Bạn Lan gieo một con xúc xắc 8 lần liên tiếp thì thấy mặt 44 chấm xuất hiện 33 lần. Xác suất xuất hiện mặt 44 chấm là
Đáp án : B
Xác suất xuất hiện mặt 4 chấm bằng tỉ số giữa số lần xuất hiện mặt 4 chấm với tổng số lần gieo xúc xắc.
Xác suất xuất hiện mặt 44 chấm là: 3838.
Đáp án B.
Cho hình vẽ bên, với GG là trọng tâm của ΔABC.ΔABC. Tỉ số của GDGD và ADAD là
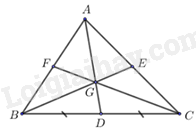
Đáp án : A
Dựa vào tính chất của trọng tâm.
Vì D là trung điểm của BC nên AD là đường trung tuyến của tam giác ABC.
G là trọng tâm của ΔABCΔABC nên AG=23ADAG=23AD hay AGAD=23AGAD=23.
Do đó: GDAD=AD−AGAD=1−AGAD=1−23=13GDAD=AD−AGAD=1−AGAD=1−23=13.
Đáp án A.
Cho hình vẽ, chọn câu đúng?

Đáp án : A
Dựa vào kiến thức đường vuông góc và đường xiên.
Đường vuông góc kẻ từ AA đến MQMQ là AIAI nên A đúng.
Đáp án A.
Tam giác ABC có AB = AC và ˆA=2ˆBˆA=2ˆB có dạng đặc biệt nào?
Đáp án : D
Chứng minh tam giác ABC cân tại A.
Dựa vào định lí tổng ba góc của một tam giác bằng 18001800 để tính các góc của tam giác ABC.
Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A. (1)
Suy ra ˆB=ˆCˆB=ˆC.
Áp dụng định lí tổng ba góc của một tam giác bằng 18001800 vào tam giác ABC, ta có:
ˆA+ˆB+ˆC=180oˆA+ˆB+ˆC=180o.
Mà ˆA=2ˆBˆA=2ˆB, ˆB=ˆCˆB=ˆC nên 2ˆB+ˆB+ˆB=180o2ˆB+ˆB+ˆB=180o
4ˆB=18004ˆB=1800 suy ra ˆB=1800:4=450ˆB=1800:4=450
Suy ra ˆA=2.450=900ˆA=2.450=900 nên tam giác ABC vuông tại A. (2)
Từ (1) và (2) suy ra tam giác ABC vuông cân tại A.
Đáp án D.
Cho ΔABCΔABC và ΔDEFΔDEF có ˆA=ˆD=900ˆA=ˆD=900, BC = EF. ΔABC=ΔDEFΔABC=ΔDEF theo trường hợp cạnh huyền – góc nhọn nếu bổ sung thêm điều kiện:
Đáp án : B
Dựa vào trường hợp bằng nhau cạnh huyền – góc nhọn của hai tam giác.
Để ΔABC=ΔDEFΔABC=ΔDEF theo trường hợp cạnh huyền góc nhọn thì BC = EF và ˆB=ˆEˆB=ˆE hoặc ˆC=ˆFˆC=ˆF.
Vậy ta chọn đáp án B.
Đáp án B.
Tìm x, biết:
a) 112+x=−1112112+x=−1112
b) 2x−127=32x−12x−127=32x−1
a) Sử dụng quy tắc tính với phân số.
b) Sử dụng tính chất của tỉ lệ thức.
a) 112+x=−1112112+x=−1112
x=−1112−112x=−11−112x=−1212=−1
Vậy x = -1
b) 2x−127=32x−1
(2x−1)2=27.3(2x−1)2=81(2x−1)2=(±9)2
TH1: 2x−1=9
2x=10x=5
TH2: 2x−1=−9
2x=−8x=−4
Vậy phương trình có nghiệm là x=5 hoặc x=−4.
Cho A(x)=4x2+4x+1.
a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b) Tìm B(x) biết A(x)+B(x)=5x2+5x+1.
c) Tính A(x):(2x+1).
a) Dựa vào kiến thức về bậc, hạng tử tự do, hạng tử cao nhất để trả lời.
b) Áp dụng quy tắc cộng, trừ đa thức một biến để tìm B(x).
c) Áp dụng quy tắc chia đa thức để tính.
a) Bậc của đa thức là 2.
Hạng tử tự do là 1.
Hạng tử cao nhất của đa thức là 4.
b) Ta có: A(x)+B(x)=5x2+5x+1
B(x)=(5x2+5x+1)−(4x2+4x+1)=5x2+5x+1−4x2−4x−1=(5x2−4x2)+(5x−4x)+(1−1)=x2+x
Vậy B(x)=x2+x
c) Ta có: A(x):(2x+1)=(4x2+4x+1):(2x+1)

Vậy A(x):(2x+1)=2x+1
Cho ΔMNP vuông tại M có MN < MP, kẻ đường phân giác NI của góc MNP (I thuộc MP). Kẻ IK vuông góc với NP tại K.
a) Chứng minh ΔIMN=ΔIKN
b) Chứng minh MI<IP.
c) Gọi Q là giao điểm của đường thẳng IK và đường thẳng MN, đường thẳng NIcắt QP tại D. Chứng minh ND⊥QP và ΔQIP cân tại I.
a) Chứng minh ΔIMN=ΔIKN(cạnh huyền - góc nhọn)
b) Chứng minh IM=IK, IP > IK nên IP > IM.
c) Chứng minh I là trực tâm của tam giác QNP nên ND⊥QP.
Chứng minh ΔNQP cân tại N nên DQ = DP.
ΔQIP có ID vừa là đường cao, vừa là đường trung tuyến nên ΔQIP cân tại I

a) Xét ΔIMN và ΔIKN có:
^IMN=^IKN=900
NI chung
^MNI=^KNI (NI là đường phân giác NI của góc MNP)
suy ra ΔIMN=ΔIKN(cạnh huyền - góc nhọn) (đpcm)
b) Vì ΔIMN=ΔIKN nên IM = IK (hai cạnh tương ứng) (1)
Vì ΔIKP vuông tại K nên IP > IK (2)
Từ (1) và (2) suy ra IP > IM (đpcm)
c) Xét ΔNQP có đường cao QK và PM cắt nhau tại I nên I là trực tâm của tam giác NQP.
Do đó ND⊥QP (đpcm)
Vì ΔNQP có ND vừa là đường cao vừa là đường phân giác nên ΔNQP cân tại N.
Suy ra ND là đường trung tuyến của tam giác NQP hay QD = DP.
Xét ΔQIP có ID vừa là đường cao vừa là đường trung tuyến nên ΔQIP cân tại I.
Cho đa thức A (x) = x2+2x+2. Chứng minh đa thức không có nghiệm.
Phân tích đa thức A(x) để chứng minh A(x) > 0 với mọi x.
Do đó A(x) không có nghiệm.
Ta có:
A(x)=x2+2x+2=x2+x+x+1+1=x(x+1)+(x+1)+1=(x+1)(x+1)+1
=(x+1)2+1>0 với mọi x.
Vậy đa thức A (x) = x2+2x+2 không có nghiệm.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365