Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 2 Toán 7 Cánh diều
Đề cương ôn tập học kì 2 Toán 7 - Cánh diều
Đề thi học kì 2 Toán 7 - Đề số 1 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 2 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 3 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 4 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 5 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 6 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 7 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 8 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 9 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 10 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 11 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 12 - Cánh diều Đề thi học kì 2 Toán 7 - Đề số 13 - Cánh diềuĐề cương ôn tập học kì 2 Toán 7 - Cánh diều
A. NỘI DUNG ÔN TẬP Đại số - Đa thức một biến. Nghiệm của đa thức một biến - Phép cộng, phép trừ đa thức một biến - Phép nhân đa thức một biến - Phép chia đa thức một biến
- Đa thức một biến. Nghiệm của đa thức một biến
- Phép cộng, phép trừ đa thức một biến
- Phép nhân đa thức một biến
- Phép chia đa thức một biến
- Tổng các góc của một tam giác
- Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác
- Tam giác bằng nhau
- Các trường hợp bằng nhau của tam giác:
+ Trường hợp cạnh – cạnh – cạnh
+ Trường hợp cạnh – góc – cạnh
+ Trường hợp góc – cạnh – góc
- Tam giác cân
- Đường trung trực của một đoạn thẳng
- Tính chất ba đường trung tuyến của tam giác
- Tính chất ba đường phân giác của tam giác
- Tính chất ba đường trung trực của tam giác
-Tính chất ba đường cao của tam giác
- Thu thập, phân loại và biểu diễn dữ liệu
- Phân tích và xử lí dữ liệu
- Các loại biểu đồ (Biểu đồ đoạn thẳng, biểu đồ hình quạt tròn)
- Biến cố trong một số trò chơi đơn giản
- Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
Câu 1: Cho các dãy dữ liệu:
(1) Tên của mỗi bạn học sinh trong lớp 7A.
(2) Số lượng học sinh của các lớp 7 đạt điểm 10 giữa học kì 1.
(3) Số nhà của mỗi bạn học sinh lớp 7B.
(4) Số lượng nhóm nhạc yêu thích của mỗi bạn học sinh trong lớp.
Trong các dãy dữ liệu trên, dãy dữ liệu không phải là số là:
A. (1).
B. (2).
C. (3).
D. (4).
Câu 2: Cho bảng thống kê số lượt khách du lịch đến Ninh Bình trong các năm 2016, 2017, 2018:

Số lượt khách du lịch đến Ninh Bình trong năm 2018 tăng bao nhiêu phần trăm so với năm 2016 (làm tròn kết quả đến hàng phần trăm)?
A. 13,33%.
B. 13,34%.
C. 13,35%.
D. 13,36%.
Câu 3: Quan sát biểu đồ dưới đây và cho biết tỉ lệ phần trăm học sinh được điểm xuất sắc (điểm 9, 10) so với số học sinh cả lớp
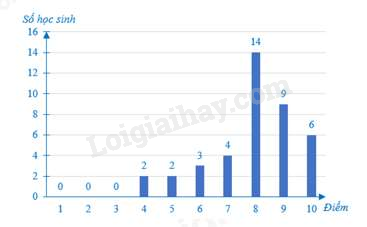
A. 37%.
B. 37,5%.
C. 38%.
D. 38,5%.
Câu 4: Tỉ lệ tăng dân số Việt Nam trong một số năm gần đây được cho trong bảng sau:

Dựa vào biểu đồ biểu diễn bảng số liệu trên, tìm x
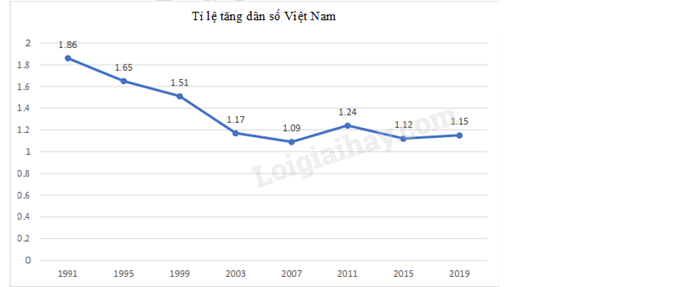
A. 1,09.
B. 1,17.
C. 1,65.
D. 1,51.
Câu 5: Biểu đồ dưới đây cho biết tỉ lệ các loại kem bán được trong một ngày của một cửa hàng kem.
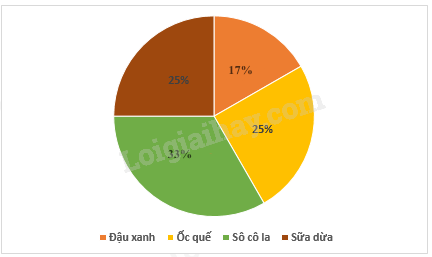
Biết rằng một ngày cửa hàng đó bán được 100 cái kem. Số lượng kem ốc quế bán được trong một ngày là bao nhiêu?
A. 20 cái.
B. 25 cái.
C. 17 cái.
D. 33 cái.
Câu 6: Có bao nhiêu đơn thức trong các biểu thức sau: −x35x3−x35x3 2+x2+x; 6x36x3; x;x; xx−1xx−1?
A. 3.
B. 4.
C. 1.
D. 5.
Câu 7: Bậc của đa thức x3−x2+7x−9x3−x2+7x−9 là
A. 1.
B. 2.
C. −9−9.
D. 3.
Câu 8: Đa thức nào là đa thức một biến?
A. 27x2−3y+1527x2−3y+15.
B. 2022x3−x2+152022x3−x2+15.
C. 5xy−x3+15xy−x3+1.
D. xyz−2xy+5xyz−2xy+5.
Câu 9: Thu gọn đa thức P = x3y – 5xy3 + 2x3y + 5xy3 bằng:
A. 3x3y - 10xy3.
B. –x3y.
C. x3y + 10 xy3.
D. 3x3y.
Câu 10: Đa thức x−2x−2 có nghiệm là:
A. 1212.
B. 00.
C. −12−12.
D. 22.
Câu 11: Đa thức Q=−13x4+5x3−8x+9Q=−13x4+5x3−8x+9 có hệ số cao nhất là:
A. -8.
B. 9.
C. −13−13.
D. 5.
Câu 12: Biểu thức biểu thị chu vi của hình chữ nhật có chiều dài 9cm9cm và chiều rộng 6cm6cm là
A. 6+9(cm).6+9(cm).
B. 2.6+9(cm).
C. 6.9(cm).
D. (6+9).2(cm).
Câu 13: Sắp xếp đa thức 6x3 + 5x4 – 8x6 – 3x2 + 4 theo lũy thừa giảm dần của biến ta được:
A. 6x3 + 5x4 – 8x6 – 3x2 + 4
B. –8x6 + 5x4 –3x2 + 4 + 6x3
C. –8x6 + 5x4 +6x3 + 4 –3x2
D. –8x6 + 5x4 +6x3 –3x2 + 4
Câu 14: Cho hai đa thức f(x) = 5x4 + x3 – x2 + 1 và g(x) = –5x4 – x2 + 2.
Tính h(x) = f(x) + g(x) và tìm bậc của h(x). Ta được:
A. h(x)= x3 – 1 và bậc của h(x) là 3
B. h(x)= x3 – 2x2 +3 và bậc của h(x) là 3
C. h(x)= x4 +3 và bậc của h(x) là 4
D. h(x)= x3 – 2x2 +3 và bậc của h(x) là 5
Câu 15: Tích của hai đơn thức 6x2 và 2x là
A. −12x3.
B. 12x3.
C. 12x2.
D. 8x3.
Câu 16: Trong một hộp có bốn tấm thẻ ghi số 1; 2; 3; 6. Rút ngẫu nhiên một tấm thẻ từ trong hộp. Đâu là biến cố chắc chắc
A. Rút được thẻ ghi số là số nguyên tố.
B. Rút được thẻ ghi số nhỏ hơn 7.
C. Rút được thẻ ghi số lớn hơn 5.
D. Rút được thẻ ghi số lá số chẵn.
Câu 17: Một hộp bút màu có nhiều màu: màu xanh, màu vàng, màu đỏ, màu đen, màu hồng, màu cam. Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả?
A. 3.
B. 4.
C. 5.
D. 6.
Câu 18: Trong trò chơi ô cửa bí mật, có 3 ô cửa 1; 2; 3 và người ta đặt phần thưởng sau một ô cửa. Người chơi sẽ chọn ngẫu nhiên một ô cửa trong ba ô cửa và nhận phần thưởng sau ô cửa đó. Xác suất để người chơi chọn được ô cửa có phần thưởng là
A. 12.
B. 23.
C. 13.
D. 31.
Câu 19: Chon ngẫu nhiên 1 số trong 4 số sau: 7; 8; 26; 101. Xác xuất để chọn được số chia hết cho 5 là:
A. 0.
B. 1.
C. 2.
D. 4.
Câu 20: Kết quả xếp loại học tập cuối học kỳ I của học sinh khối 7 được cho ở biểu đồ bên.
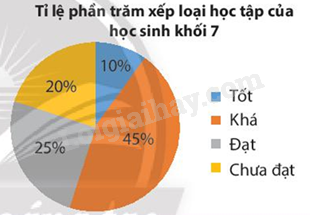
Gặp ngẫu nhiên một học sinh khối 7 thì xác xuất học sinh đó được xếp loại học lực nào là thấp nhất?
A. Tốt.
B. Khá.
C. Đạt.
D. Chưa đạt.
Câu 21: Cho ΔABC biết rằng ˆA=80∘;ˆC=40∘;ˆB=60∘. Khi đó ta có
A. AB<AC<BC.
B. AC<BC<AB.
C. AB>AC>BC.
D.AC>BC>AB.
Câu 22: Cho hình vẽ, chọn câu sai
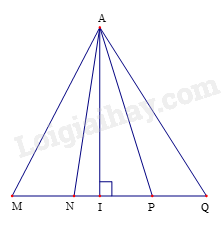
A. Đường vuông góc kẻ từ A đến MQ là AI.
B. Đường xiên kẻ từ M đến AI là MA.
C. Đường xiên kẻ từ A đến MQ là AM,AN,AP,AQ.
D. Đường xiên kẻ từ Q đến AI là AQ,AP.
Câu 23: Bộ ba nào sau đây có thể là độ dài ba cạnh của một tam giác?
A. 3cm;3cm;9cm.
B. 1,2cm;1cm;2,4cm.
C. 4cm;5cm;6cm.
D. 4cm;4cm;8cm.
Câu 24: Các đường cao của tam giác ABC cắt nhau tại Hthì
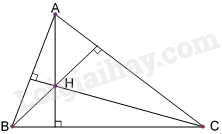
A. điểm H là trọng tâm của tam giác ABC.
B. điểm H cách đều ba cạnh tam giác ABC.
C. điểm H cách đều ba đỉnh A,B,C.
D. điểm H là trực tâm của tam giác ABC.
Câu 25: Cho hình vẽ bên, với G là trọng tâm của ΔABC. Tỉ số của GDvàAGlà
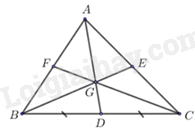
A. 13.
B. 23.
C. 2.
D. 12.
Câu 26: Cho ΔABC có: ˆA=350. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của ^ACB. Số đo các góc ^ABC;^ACBlà:
A. ^ABC=720;^ACB=730.
B. ^ABC=730;^ACB=720.
C. ^ABC=750;^ACB=700.
D. ^ABC=700;^ACB=750.
Câu 27: Cho hình vẽ sau.
Biết MG = 3cm. Độ dài đoạn thẳng MR bằng:
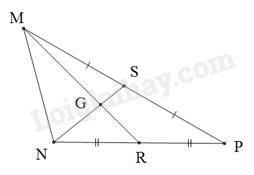
A. 4,5 cm.
B. 2 cm.
C. 3 cm.
D. 1 cm.
Câu 28: Giao điểm của ba đường trung tuyến trong một tam giác:
A. Cách đều 3 đỉnh của tam giác đó.
B. Là điểm luôn thuộc một cạnh của tam giác đó.
C. Là trọng tâm của tam giác đó.
D. Cách đều 3 cạnh của tam giác đó.
Câu 29: Cho hình vẽ bên. So sánh AB, BC, BD ta được:
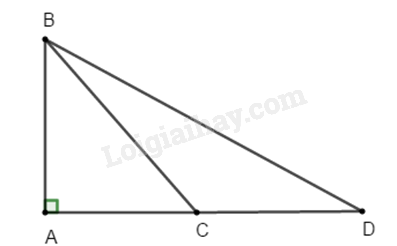
A. AB > BC > BD.
B. BD > BC > AB.
C. BC > BD > AB.
D. BD < AB < CB.
Câu 30: Độ dài hai cạnh của một tam giác là 3cm và 11cm. Trong các số đo sau, số đo nào sau đây là độ dài cạnh thứ 3 của tam giác:
A. 8 cm.
B. 7cm.
C. 6cm.
D. 9cm.
Câu 31: Cho ΔABC và ΔDEF có ˆA=ˆD=900,BC=EF,ΔABC=ΔDEF (cạnh huyền – góc nhọn) nếu bổ sung thêm điều kiện:
A. AB = EF.
B. ˆB=ˆE.
C. AC = DF.
D. Đáp án khác.
Câu 32: Khẳng định nào sau đây không đúng:
A. Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
B. Trong tam giác cân hai góc ở đáy bằng nhau.
C. Tam giác có hai góc bằng nhau là tam giác đều.
D. Trong tam giác đều mỗi góc 600.
Câu 33: ΔMNP cân tại M. Biết góc N có số đo bằng 700. Số đo góc M bằng:
A. 700.
B. 400.
C. 500.
D. 800.
Câu 34: Cho hai tam giác bằng nhau: Tam giác ABC và tam giác có ba đỉnh là M, N, P. Biết ˆA=ˆM;ˆB=ˆN. Hệ thức bằng nhau giữa hai tam giác theo thứ tự đỉnh tương ứng là:
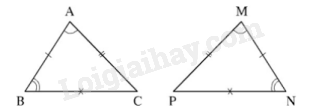
A. ΔABC=ΔNMP.
B. ΔABC=ΔMNP.
C. ΔBAC=ΔPMN.
D. ΔCAB=ΔMNP.
Câu 35: Cho ΔABC có AM là đường phân giác đồng thời là đường cao, khi đó ΔABC là tam giác gì?
A. Tam giác cân.
B. Tam giác vuông.
C. Tam giác đều.
D. Tam giác vuông cân.
Bài 1. Cho A(x)=2x4+4x3−3x2−4x+1.
a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b) Tìm B(x) biết A(x)+B(x)=2x3−x2+5
c) Tính A(x):(x2−1).
Bài 2. Cho A(x)=4x2+4x+1.
a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b) Tìm B(x) biết A(x)+B(x)=5x2+5x+1.
c) Tính A(x):(2x+1).
Bài 3. Biểu đồ đoạn thẳng bên biểu diễn tổng sản phẩm quốc nội (GDP) của nước ta trong giai đoạn từ năm 2014 đến năm 2019.
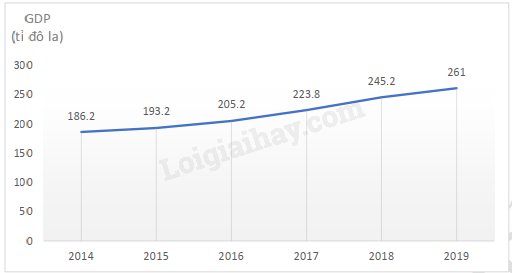
a) GDP năm 2016 là bao nhiêu?
b) GDP của nước ta có xu hướng tăng hay giảm?
c) So với năm 2014, GDP năm 2019 đã tăng bao nhiêu tỉ đô la.
d) GDP năm 2017 đã tăng bao nhiêu phần trăm so với năm 2015?
Bài 4. Biểu đồ hình quạt tròn bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) số nhân viên ở các bộ phận của một công ty.
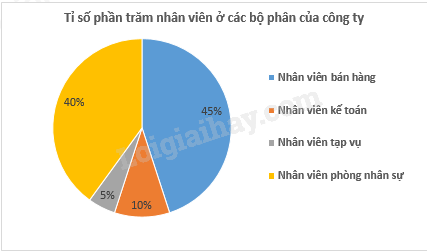
a) Bộ phận nào có ít nhân viên nhất?
b) Số nhân viên bộ phận bán hàng nhiều gấp bao nhiêu lần bộ phận kế toán?
c) Biết công ty có 240 nhân viên. Tính số nhân viên của mỗi bộ phận.
d) Biết tổng mức thưởng Tết của bộ phận kế toán là 25 200 000 đồng và mỗi nhân viên được thưởng như nhau. Tính tổng mức thưởng Tết của bộ phận nhân sự.
Bài 5. Lan và Hoa mỗi người gieo một con xúc xắc.
a) Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là một số lớn hơn 1” là biến cố gì?
b) Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7” là biến cố gì?
Bài 6. Chọn ngẫu nhiên một số trong bốn số 11;12;13 và 14. Tìm xác suất để:
a) Chọn được số chia hết cho 5.
b) Chọn được số có hai chữ số.
c) Chọn được số nguyên tố.
d) Chọn được số chia hết cho 6.
Bài 7. Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,2,3,.....,12; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xét biến cố “Số xuất hiện trên thẻ được rút ra 1 số là hợp số”. Tìm xác suất của biến cố trên.
Bài 8. Cho ΔABC vuông tại A có AB<AC, kẻ đường phân giác BD của ^ABC,(D∈AC). Kẻ DM vuông góc với BC tại M.
a) Chứng minh ΔDAB=ΔDMB.
b) Chứng minh AD<DC
c) Gọi K là giao điểm của đường thẳng DM và đường thẳng AB, đường thẳng BD cắt KC tại N. Chứng minh BN⊥KC và ΔKDC cân tại B.
Bài 9. Cho ΔMNPcân tại M (ˆM<900). Kẻ NH ⊥MP (H∈MP), PK ⊥MN (K∈MN). NH và PK cắt nhau tại E.
a) Chứng minh ΔNHP=ΔPKN
b) Chứng minh ΔENP cân.
c) Chứng minh ME là đường phân giác của góc NMP.
Bài 10. Cho ΔABC cân tại A, có đường trung tuyến AM.
a) Chứng minh ΔABM=ΔACM.
b) Từ điểm M vẽ đường thẳng ME vuông góc với AB(E∈AB) và vẽ đường thẳng MF vuông góc với AC(F∈AC). Chứng minh ME=MF.
Bài 11*. Tính giá trị của biểu thức: N=xy2z3+x2y3z4+x3y4z5+...+x2022y2023z2024, tại x = -1, y = -1, z = -1
Bài 12*. Cho biểu thức A=34+89+1516+...+999910000. Chứng minh rằng A < 99
-------- Hết --------
|
Câu 1. A |
Câu 2. C |
Câu 3. B |
Câu 4. A |
Câu 5. D |
|
Câu 6. A |
Câu 7. D |
Câu 8. B |
Câu 9. D |
Câu 10. D |
|
Câu 11. C |
Câu 12. D |
Câu 13. D |
Câu 14. B |
Câu 15. B |
|
Câu 16. B |
Câu 17. D |
Câu 18. C |
Câu 19. A |
Câu 20. A |
|
Câu 21. A |
Câu 22. D |
Câu 23. C |
Câu 24. D |
Câu 25. D |
|
Câu 26. C |
Câu 27. A |
Câu 28. C |
Câu 29. B |
Câu 30. D |
|
Câu 31. B |
Câu 32. C |
Câu 33. B |
Câu 34. B |
Câu 35. A |
Bài 1. Cho A(x)=2x4+4x3−3x2−4x+1.
a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b) Tìm B(x) biết A(x)+B(x)=2x3−x2+5
c) Tính A(x):(x2−1).
Phương pháp
a) Dựa vào kiến thức về bậc, hạng tử tự do, hạng tử cao nhất để trả lời.
b) Áp dụng quy tắc cộng, trừ đa thức một biến để tìm B(x).
c) Áp dụng quy tắc chia đa thức cho đa thức để tính.
Lời giải
a) Bậc của đa thức là 4.
Hạng tử tự do là 1.
Hạng tử cao nhất của đa thức là 2.
b) Ta có: A(x)+B(x)=2x3−x2+5
B(x)=(2x3−x2+5)−A(x)=(2x3−x2+5)−(2x4+4x3−3x2−4x+1)=2x3−x2+5−2x4−4x3+3x2+4x−1=−2x4+(2x3−4x3)+(−x2+3x2)+4x+(5−1)=−2x4−2x3+2x2+4x+4
Vậy B(x)=−2x4−2x3+2x2+4x+4
c) Ta có:
A(x):(x2−1)=(2x4+4x3−3x2−4x+1):(x2−1)

Vậy A(x):(x2−1)=2x2+4x−1
Bài 2. Cho A(x)=4x2+4x+1.
a) Xác định bậc, hạng tử tự do, hạng tử cao nhất của đa thức.
b) Tìm B(x) biết A(x)+B(x)=5x2+5x+1.
c) Tính A(x):(2x+1).
Phương pháp
a) Dựa vào kiến thức về bậc, hạng tử tự do, hạng tử cao nhất để trả lời.
b) Áp dụng quy tắc cộng, trừ đa thức một biến để tìm B(x).
c) Áp dụng quy tắc chia đa thức để tính.
Lời giải
a) Bậc của đa thức là 2.
Hạng tử tự do là 1.
Hạng tử cao nhất của đa thức là 4.
b) Ta có: A(x)+B(x)=5x2+5x+1
B(x)=(5x2+5x+1)−(4x2+4x+1)=5x2+5x+1−4x2−4x−1=(5x2−4x2)+(5x−4x)+(1−1)=x2+x
Vậy B(x)=x2+x
c) Ta có: A(x):(2x+1)=(4x2+4x+1):(2x+1)
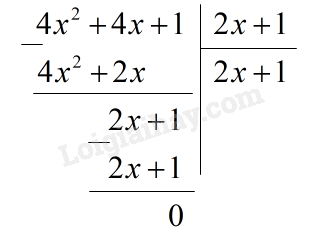
Vậy A(x):(2x+1)=2x+1
Bài 3. Biểu đồ đoạn thẳng bên biểu diễn tổng sản phẩm quốc nội (GDP) của nước ta trong giai đoạn từ năm 2014 đến năm 2019.
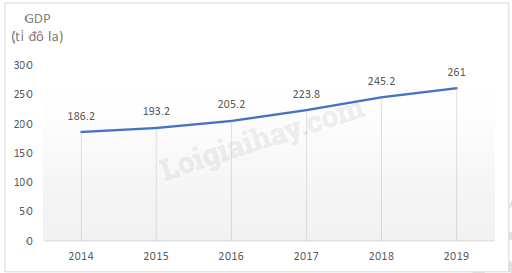
a) GDP năm 2016 là bao nhiêu?
b) GDP của nước ta có xu hướng tăng hay giảm?
c) So với năm 2014, GDP năm 2019 đã tăng bao nhiêu tỉ đô la.
d) GDP năm 2017 đã tăng bao nhiêu phần trăm so với năm 2015?
Phương pháp
a, b) Quan sát biểu đồ để trả lời.
c, d) Quan sát biểu đồ kết hợp tính toán để trả lời.
Lời giải
a) Quan sát biểu đồ ta thấy GDP năm 2016 là 205,0 tỉ đô la.
b) Quan sát biểu đồ ta thấy đường thẳng đi lên nên GDP của nước ta có xu hướng tăng.
c) So với năm 2014, GDP năm 2019 đã tăng là:
261 – 186,2 = 74,8 9 (tỉ đô la).
d) Tỉ số phần trăm của GDP năm 2017 và GDP năm 2015 là:
223,8.100193,2%≈115,84%.
Vậy GDP năm 2017 đã tăng khoảng 15,84% so với năm 2015.
Bài 4. Biểu đồ hình quạt tròn bên biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) số nhân viên ở các bộ phận của một công ty.
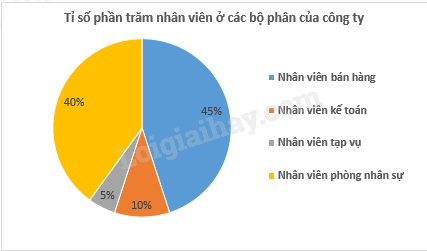
a) Bộ phận nào có ít nhân viên nhất?
b) Số nhân viên bộ phận bán hàng nhiều gấp bao nhiêu lần bộ phận kế toán?
c) Biết công ty có 240 nhân viên. Tính số nhân viên của mỗi bộ phận.
d) Biết tổng mức thưởng Tết của bộ phận kế toán là 25 200 000 đồng và mỗi nhân viên được thưởng như nhau. Tính tổng mức thưởng Tết của bộ phận nhân sự.
Phương pháp
a) Quan sát biểu đồ để trả lời.
b, c, d) Quan sát biểu đồ kết hợp tính toán để trả lời.
Lời giải
a) Quan sát biểu đồ ta thấy bộ phận tạp vụ có ít nhân viên nhất.
b) Tỉ số giữa số nhân viên bộ phận bán hàng và số nhân viên bộ phận kế toán là:
45%:10%=4510=4,5.
Vậy số nhân viên bộ phận bán hàng nhiều gấp 4,5 lần bộ phận kế toán.
c) Số nhân viên bán hàng là: 240.45%=108 (nhân viên)
Số nhân viên kế toán là: 240.10%=24 (nhân viên)
Số nhân viên tạp vụ là: 240.5%=12 (nhân viên)
Số nhân viên phòng nhân sự là: 240.40%=96 (nhân viên)
d) Mức thưởng Tết của mỗi nhân viên là:
25200000:24=1050000 (đồng)
Tổng mức thưởng Tết của bộ phận nhân sự là:
1050000.96=100800000 (đồng)
Bài 5. Lan và Hoa mỗi người gieo một con xúc xắc.
a) Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là một số lớn hơn 1” là biến cố gì?
b) Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7” là biến cố gì?
Phương pháp
Xác định số kết quả xảy ra của biến cố đó, ta xác định được biến cố đó là biến cố gì.
+) Biến cố chắc chắn: là biến cố biết trước được luôn xảy ra.
+) Biến cố không thể: là biến cố biết trước được không bao giờ xảy ra.
+) Biến cố ngẫu nhiên: là biến cố không thể biết trước được có xảy ra hay không.
Lời giải
a) Vì 1 con xúc xắc có số chấm là: 1; 2; 3; 4; 5; 6.
Tổng số chấm xuất hiện trên hai con xúc xắc có giá trị nhỏ nhất là: 1 + 1 = 2 > 1.
Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là một số lớn hơn 1” là biến cố chắc chắn.
b) Biến cố này là biến cố ngẫu nhiên vì ta không thể biết trước nó có xảy ra hay không. Chẳng hạn, nếu ta gieo được hai con xúc xắc là 3 và 4 thì biến cố xảy ra; còn nếu gieo hai con xúc xắc là 2 và 4 thì biến cố không xảy ra .
Bài 6. Chọn ngẫu nhiên một số trong bốn số 11;12;13 và 14. Tìm xác suất để:
a) Chọn được số chia hết cho 5.
b) Chọn được số có hai chữ số.
c) Chọn được số nguyên tố.
d) Chọn được số chia hết cho 6.
Phương pháp
Kiểm tra khả năng xảy ra của biến cố.
Lời giải
a) Không có số nào chia hết cho 5 nên xác suất để chọn được số chia hết cho 5 là 0.
b) Cả 4 số đều là số có hai chữ số nên xác suất để chọn được số có hai chữ số là 1.
c) Có hai số (11; 13) là số nguyên tố nên xác suất để chọn được số nguyên tố là 24=12.
d) Có một số (12) chia hết cho 6 nên xác suất để chọn được số chia hết cho 6 là 14.
Bài 7. Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,2,3,.....,12; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xét biến cố “Số xuất hiện trên thẻ được rút ra 1 số là hợp số”. Tìm xác suất của biến cố trên.
Phương pháp
Tính số kết quả thuận lợi cho biến cố A, B, C.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với tổng số kết quả có thể.
Lời giải
Có 6 kết quả có thể xảy ra khi lấy ngẫu nhiên 1 thẻ từ hộp, đó là: 2; 3; 5; 8; 13; 21.
+) Có 4 số lẻ là 3; 5; 13; 21 nên số kết quả thuận lợi cho biến cố A là 4.
Xác suất của biến cố A: “Số ghi trên thẻ là số lẻ” là: 46=23.
+) Có 4 số nguyên tố là: 2; 3; 5; 13 nên số kết quả thuận lợi cho biến cố B là 4.
Xác suất của biến cố B: “Số ghi trên thẻ là số nguyên tố” là: 46=23.
+) Không có số chính phương trong các số trên nên số kết quả thuận lợi cho biến cố C là 0.
Xác suất của biến cố C: “Số ghi trên thẻ là số chính phương” là: 06=0.
Bài 8. Cho ΔMNP vuông tại M có MN < MP, kẻ đường phân giác NI của góc MNP (I thuộc MP). Kẻ IK vuông góc với NP tại K.
a) Chứng minh ΔIMN=ΔIKN
b) Chứng minh MI<IP.
c) Gọi Q là giao điểm của đường thẳng IK và đường thẳng MN, đường thẳng NI cắt QP tại D. Chứng minh ND⊥QP và ΔQIP cân tại I.
Phương pháp
a) Chứng minh ΔIMN=ΔIKN(cạnh huyền - góc nhọn)
b) Chứng minh IM=IK, IP > IK nên IP > IM.
c) Chứng minh I là trực tâm của tam giác QNP nên ND⊥QP.
Chứng minh ΔNQP cân tại N nên DQ = DP.
ΔQIP có ID vừa là đường cao, vừa là đường trung tuyến nên ΔQIP cân tại I
Lời giải
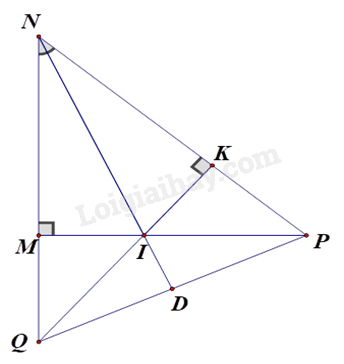
a) Xét ΔIMN và ΔIKN có:
^IMN=^IKN=900
NI chung
^MNI=^KNI (NI là đường phân giác NI của góc MNP)
suy ra ΔIMN=ΔIKN(cạnh huyền - góc nhọn) (đpcm)
b) Vì ΔIMN=ΔIKN nên IM = IK (hai cạnh tương ứng) (1)
Vì ΔIKP vuông tại K nên IP > IK (2)
Từ (1) và (2) suy ra IP > IM (đpcm)
c) Xét ΔNQP có đường cao QK và PM cắt nhau tại I nên I là trực tâm của tam giác NQP.
Do đó ND⊥QP (đpcm)
Vì ΔNQP có ND vừa là đường cao vừa là đường phân giác nên ΔNQP cân tại N.
Suy ra ND là đường trung tuyến của tam giác NQP hay QD = DP.
Xét ΔQIP có ID vừa là đường cao vừa là đường trung tuyến nên ΔQIP cân tại I.
Bài 9. Cho ΔMNP cân tại M (ˆM<900). Kẻ NH ⊥MP (H∈MP), PK ⊥MN (K∈MN). NH và PK cắt nhau tại E.
a) Chứng minh ΔNHP=ΔPKN
b) Chứng minh ΔENP cân.
c) Chứng minh ME là đường phân giác của góc NMP.
Phương pháp
a) Chứng minh ΔNHP=ΔPKN theo trường hợp cạnh huyền – góc nhọn.
b) Chứng minh ^P1=^N1 nên ΔENP cân.
c) Chứng minh MK = MH.
Chứng minh ΔMEK=ΔMEH (cạnh huyền – cạnh góc vuông) suy ra ^M1=^M2.
Do đó ME là đường phân giác của góc NMP.
Lời giải
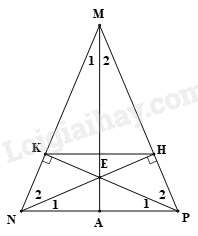
a) Xét ΔNHP và ΔPKN vuông tại H và K có:
^NPH=^PNK (vì ΔMNP cân tại M)
NP chung
Suy ra ΔNHP=ΔPKN (cạnh huyền – góc nhọn) (đpcm)
b) Vì ΔNHP=ΔPKNnên ^N1=^P1.
Do đó ΔENP cân tại E (đpcm)
c) Ta có:
MK=MN−NK (vì K thuộc MN)
MH=MP−HP (vì H thuộc MP)
Mà MN=MP (vì ΔMNP cân tại M)
NK=PH (vì ΔNHP=ΔPKN)
suy ra MK=MH.
Xét ΔMEK và ΔMEH vuông tại K và H có:
ME là cạnh chung
MK = MH (cmt)
Suy ra ΔMEK=ΔMEH (ch – cgv)
Suy ra ^M1=^M2 suy ra ME là tia phân giác của góc NMP (đpcm)
Bài 10. Cho ΔABC cân tại A, có đường trung tuyến AM.
a) Chứng minh ΔABM=ΔACM.
b) Từ điểm M vẽ đường thẳng ME vuông góc với AB(E∈AB) và vẽ đường thẳng MF vuông góc với AC(F∈AC). Chứng minh ME=MF.
Phương pháp
a) Chứng minh ΔABM=ΔACM theo trường hợp cạnh – góc – cạnh.
b) Chứng minh ΔBEM=ΔCFM suy ra ME = MF.
Lời giải
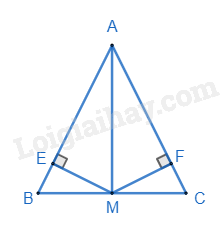
a) Vì tam giác ABC cân tại A nên ta có AB=AC,ˆB=ˆC.
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC, ta có: BM = MC.
Xét ΔABM và ΔACM có:
AB=AC (cmt)
ˆB=ˆC (cmt)
BM=CM (cmt)
Suy ra ΔABM=ΔACM (c.g.c) (đpcm)
b) Xét ΔBEM và ΔCFM có:
ˆE=ˆF=90o (gt)
ˆB=ˆC (cmt)
BM=CM (cmt)
Suy ra ΔBEM=ΔCFM (ch.gn)
Suy ra ME = MF (hai cạnh tương ứng).
Bài 11*. Tính giá trị của biểu thức: N=xy2z3+x2y3z4+x3y4z5+...+x2022y2023z2024, tại x = -1, y = -1, z = -1
Phương pháp
Biến đổi N thành N=xyz.yz2+x2y2z2.yz2+x3y3z3.yz2+...+x2022y2022z2022.yz2
Thay giá trị của yz2 theo y = -1, z = -1 vào N để rút gọn N.
Thay giá trị của xyz theo x = -1, y = -1, z = -1 để tính giá trị của N.
Lời giải
Ta có N=xyz.yz2+x2y2z2.yz2+x3y3z3.yz2+...+x2022y2022z2022.yz2
Tại y = -1, z = -1 ta được yz2=−1.(−1)2=−1.
Thay vào N, ta được:
N=−xyz−x2y2z2−x3y3z3−...−x2022y2022z2022
=−(xyz)−(xyz)2−(xyz)3−...−(xyz)2022
Tại x = -1, y = -1, z = -1 ta được xyz=(−1).(−1).(−1)=−1.
Thay vào N, ta được:
N=−(−1)−(−1)2−(−1)3−...−(−1)2022
N=1−1+1−1+...+1−1=0
Vậy N = 0
Bài 12*. Cho biểu thức A=34+89+1516+...+999910000 . Chứng minh rằng A < 99
Phương pháp
Biến đổi các phân số trong A thành hiệu của 1 trừ đi phân số có tử số là 1. (ví dụ: 34=1−14).
Nhóm các số 1 thành 1 nhóm, các phân số còn lại thành một nhóm, ta được
A=99−(122+132+142+...+11002).
Chứng minh 122+132+142+...+11002>0 nên A=99−(122+132+142+...+11002)<0hay A < 99.
Lời giải
Ta có:
A=34+89+1516+...+999910000
=(1−14)+(1−19)+(1−116)+...+(1−110000)
=(1−122)+(1−132)+(1−142)+...+(1−11002)
= 99−(122+132+142+...+11002)=99−B
với B = 122+132+142+...+11002 > 0 nên A < 99.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365