Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 1 Toán 7 Cánh diều
Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 11
Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 12 Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 13 Đề thi giữa kì 1 Toán 7 - Đề số 10 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 9 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 8 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 7 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 6 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 5 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 4 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 3 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 2 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 1 - Cánh diềuĐề thi giữa kì 1 Toán 7 Cánh diều - Đề số 11
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Kết quả phép tính 0,5+3−4 là
74.
14.
−14.
−198.
Đáp án : C
Đưa 0,5 về phân số, thực hiện phép cộng với hai số hữu tỉ.
Ta có: 0,5+3−4=12+−34=24+−34=−14.
Đáp án C.
Cách biểu diễn số 34 trên trục số nào dưới đây đúng?

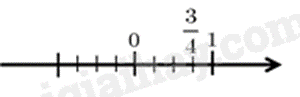


Đáp án : B
Dựa vào cách biểu diễn số hữu tỉ trên trục số.
Biểu diễn số hữu tỉ 34 trên trục số.
Chia đoạn thẳng đơn vị thành 4 phần bằng nhau. Lấy một đoạn làm đơn vị mới (đơn vị mới bằng 14 đơn vị cũ)
Số hữu tỉ được biểu diễn bằng điểm nằm bên phải gốc O, cách gốc O một đoạn bằng 3 đơn vị mới.
Do đó hình B biểu diễn số 34.

Đáp án B.
Tập hợp số hữu tỉ được kí hiệu là
N.
Z.
N∗.
Q.
Đáp án : D
Dựa vào kí hiệu các tập hợp.
Tập hợp các số hữu tỉ được kí hiệu là Q.
Đáp án D.
Giá trị của (23)2 bằng
4.
8.
64.
16.
Đáp án : C
Dựa vào kiến thức lũy thừa của lũy thừa: (am)n=am.n.
Ta có: (23)2=23.2=26=64.
Đáp án C.
Trong các số hữu tỉ −12;−34;0;1;12;43 có bao nhiêu số hữu tỉ dương?
2.
3.
4.
5.
Đáp án : B
Số hữu tỉ dương là các số hữu tỉ lớn hơn 0.
Có 3 số hữu tỉ dương, đó là: 1;12;43.
Đáp án B.
Điền kí hiệu thích hợp vào ô trống: −76...Q
∈.
∉.
=.
<.
Đáp án : A
Dựa vào kiến thức về các kí hiệu ∈,∉.
Vì −76 là số hữu tỉ nên −76∈Q.
Đáp án A.
Số nghịch đảo của số − 0,7 là
0,7.
−710.
−107.
107.
Đáp án : C
Hai số được gọi là nghịch đảo nếu tích của chúng bằng 1.
Ta có: −0,7=−710; (−710).(−107)=1 nên số nghịch đảo của −0,7 là −107.
Đáp án C.
Kết quả của phép tính (−34)8.(−34)2 là
(−34)6.
(−34)10.
(−34)4.
(−34)16.
Đáp án : B
Sử dụng kiến thức tích hai lũy thừa cùng cơ số: am.an=am+n.
Ta có:
(−34)8.(−34)2=(−34)8+2=(−34)10.
Đáp án B.
Tìm số đo x trong hình vẽ bên cạnh.

90∘.
60∘.
45∘.
30∘.
Đáp án : D
Dựa vào kiến thức về hai góc đối đỉnh và hai góc kề nhau.

Ta đặt góc y như hình vẽ.
Vì y+60∘=90∘ nên y=90∘−60∘=30∘.
Vì x và y là hai góc đối đỉnh nên x=y=30∘.
Đáp án D.
Hình lăng trụ đứng tam giác có số cạnh là
8.
12.
9.
10.
Đáp án : C
Dựa vào đặc điểm của hình lăng trụ đứng tam giác.
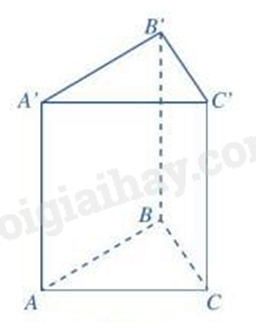
Hình lăng trụ đứng tam giác có 9 cạnh.
Đáp án C.
Hình nào sau đây là hình lăng trụ đứng tứ giác?

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Đáp án : B
Dựa vào kiến thức về hình lăng trụ đứng tứ giác.
Hình 2 là hình lăng trụ đứng tứ giác.
Đáp án B.
Cho hình bên. Hãy chọn khẳng định đúng.

^xBy và ^yBz là hai góc kề nhau.
^xBz và ^yBz là hai góc kề bù.
^yBz và ^zAt là hai góc kề nhau.
^ABy và ^xBz là hai góc đối đỉnh.
Đáp án : A
Dựa vào kiến thức về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.
^xBy và ^yBz là hai góc kề nhau là khẳng định đúng.
^xBz và ^yBz không phải là hai góc kề bù.
^yBz và ^zAt không phải là hai góc kề nhau.
^ABy và ^xBz không phải là hai góc đối đỉnh.
Đáp án A.
Thực hiện phép tính
a) 125+335
b) (−59).311+(−49).311
c) 2023−(13)2.32
d) 516.2771255.911
a) Đưa các hỗn số về phân số để thực hiện phép tính với số hữu tỉ.
b) Sử dụng tính chất phân phối của phép nhân đối với phép cộng.
c) Thực hiện phép tính với lũy thừa.
d) Thực hiện phép tính với lũy thừa.
a) 125+335
=75+185=255=5
b) (−59).311+(−49).311
=311.[(−59)+(−49)]=311.(−1)=−311
c) 2023−(13)2.32
=2023−19.9=2023−1=2022
d) 516.2771255.911=516.(33)7(53)5.(32)11=516.321515.322=53
Tìm x, biết:
a) x−23=−13
b) 73.x+47=−37
Sử dụng quy tắc chuyển vế và thực hiện phép tính với số hữu tỉ để tìm x.
a) x−23=−13
x=(−13)+23x=13
Vậy x=13.
b) 73.x+47=−37
73.x=(−37)−4773.x=−1x=−1:73x=−37
Vậy x=−37.
Một cái bể hình hộp chữ nhật và một cái chai có kích thước và thể tích như hình bên dưới. Cho biết một chai nước đầy rót hết vào bể có thể tích là 2000cm3.
Tính chiều cao mực nước sau khi rót hết một chai nước vào bể.
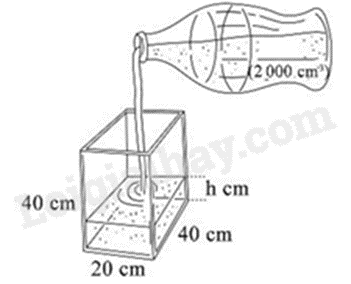
Dựa vào công thức tính thể tích của hình hộp chữ nhật suy ra chiều cao.
Vì V=h.S nên h=VS (với V là thể tích; h là chiều cao, S là diện tích đáy).
Thể tích phần nước sau khi rót hết vào bể chính là thể tích của chai nước. Do đó thể tích phần nước trong bể là 2000cm3.
Vì phần nước trong bể cũng là một hình hộp chữ nhật với kích thước đáy là kích thước bể nên thể tích phần nước trong bể là:
V=h.S hay 2000=h.20.40
Do đó chiều cao mực nước sau khi rót hết một chai nước vào bể là:
h=200020.40=2,5(cm)
Vậy chiều cao mực nước sau khi rót hết một chai nước vào bể là 2,5cm.
Một cái bục hình lăng trụ đứng tứ giác có kích thước như hình vẽ bên.
a) Tính diện tích xung quanh hình lăng trụ.
b) Người ta muốn sơn tất cả các mặt của cái bục trừ mặt nằm dưới đất. Hỏi chi phí để sơn là bao nhiêu? Biết rằng để sơn mỗi mét vuông tốn 25 nghìn đồng.

a) Sử dụng công thức tính diện tích xung quanh của hình lăng trụ: Sxq = Cđáy . h.
b) Tính diện tích hai đáy.
Tính diện tích cần sơn (gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới)).
Chi phí bằng diện tích cần sơn . 25 nghìn đồng.
a) Diện tích xung quanh chiếc hộp là:
Sxq = Cđáy . h = (4 + 5 + 5 + 8) . 12 = 264 (dm2)
Diện tích 2 đáy là:
S2đáy = (5 + 8). 4 : 2 . 2 = 52 (dm2)
Các mặt cần sơn gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới) nên diện tích phần cần sơn là:
264 + 52 – 8.12 = 220 (dm2) = 2,2 (m2)
Do đó chi phí để sơn là:
2,2 . 25 = 55 (nghìn đồng).
Quan sát hình vẽ
a) Góc đối đỉnh với ^yOv là góc nào?
b) Tìm số đo x của góc ^uOt?
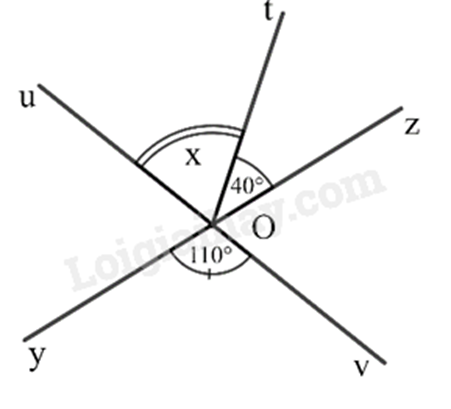
a) Dựa vào kiến thức về hai góc đối đỉnh.
b) Dựa vào kiến thức về hai góc đối đỉnh và hai góc kề nhau để tìm x.
a) Góc đối đỉnh với góc ^yOv là góc ^uOz
b) Vì hai góc ^yOv và ^uOz là hai góc đối đỉnh nên ^yOv=^uOz=110∘
Ta có: Vì ^uOt kề với ^tOz nên ^uOt+^tOz=^uOz
hay ^uOt+40∘=110∘
Suy ra ^uOt=110∘−40∘=70∘
Chào mừng năm học mới, Thế giới di dộng giảm giá một dòng máy tính bảng như sau: Đợt I giảm 10%, đợt II giảm 8% so với giá sau khi đã giảm ở đợt I. Chiếc máy tính bảng giá ban đầu là 20 000 000 đồng. Hỏi sau 2 đợt giảm giá chiếc máy tính bảng bán với giá bao nhiêu?
Dựa vào đề bài để viết phép tính.
Giá của chiếc máy tính bảng sau 2 đợt giảm là
20000000.(100%−10%).(100%−8%)=16560000 (đồng)
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365