Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 1 Toán 7 Cánh diều
Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 12
Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 13 Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 11 Đề thi giữa kì 1 Toán 7 - Đề số 10 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 9 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 8 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 7 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 6 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 5 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 4 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 3 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 2 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 1 - Cánh diềuĐề thi giữa kì 1 Toán 7 Cánh diều - Đề số 12
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Trong các số −13;0;1,5;−(−12)−13;0;1,5;−(−12), các số hữu tỉ âm là:
1,5;0.
−13.
−13;−(−12).
−(−12).
Đáp án : B
Số hữu tỉ âm là các số hữu tỉ nhỏ hơn 0.
Có 1 số hữu tỉ âm là: −13.
Đáp án B.
Số đối của số hữu tỉ −235 dưới dạng phân số là:
235.
−135.
135.
−2,6.
Đáp án : C
Số đối của số hữu tỉ a là – a.
Ta có: −235=−135 nên số đối của −235 là −(−135)=135.
Đáp án C.
Chọn khẳng định đúng trong các khẳng định sau.
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.
Số 0 là số hữu tỉ dương.
Số nguyên âm không phải là số hữu tỉ âm.
Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm.
Đáp án : A
Dựa vào kiến thức về số hữu tỉ.
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương nên A đúng.
Số 0 không phải số hữu tỉ âm cũng không phải số hữu tỉ dương nên B sai.
Số nguyên âm cũng là số hữu tỉ âm nên C sai.
Tập hợp Q gồm các số hữu tỉ dương, các số hữu tỉ âm và số 0 nên D sai.
Đáp án A.
Cho số hữu tỉ x. Chọn khẳng định đúng?
xm.xn=xm.n.
(x.y)n=xn+yn.
xm:xn=xm−n(x≠0;m≥n).
(xm)n=xm+n.
Đáp án : C
Dựa vào kiến thức về lũy thừa với số mũ tự nhiên.
Ta có:
+) xm.xn=xm+n nên A sai.
+) (x.y)n=xn.yn nên B sai.
+) xm:xn=xm−n(x≠0;m≥n) nên khẳng định C đúng.
+) (xm)n=xm.n nên khẳng định D sai.
Đáp án C.
Cho A=3n−2. Tìm điều kiện của số nguyên n để A là một số hữu tỉ.
n>2.
n<2.
n=2.
n≠2.
Đáp án : D
Một số là số hữu tỉ thì mẫu số của số đó khác 0.
Để A là một số hữu tỉ thì n−2≠0 suy ra n≠2.
Đáp án D.
Phát biểu nào sau đây đúng về hình lập phương ABCD.MNPQ.
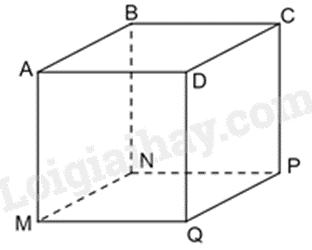
Bốn đường chéo AP,BP,CM,DB.
Ba góc vuông ở đỉnh A: góc DAB, góc DAM, góc MAB.
AM=AB=AD=AC.
Bốn mặt bên là ABCD, MNPQ, AMNB,BNPC.
Đáp án : B
Dựa vào đặc điểm của hình lập phương.
Các đường chéo của hình lập phương là AP,BQ,CM,DN nên A sai.
Ba góc vuông ở đỉnh A là: góc DAB, góc DAM, góc MAB nên B đúng.
Vì ABCD.MNPQ là hình lập phương nên AM=AB=AD. AC là đường chéo của ABCD nên AC không bằng AM. Do đó khẳng định C sai.
Bốn mặt bên của hình lập phương là ABNM, BCPN, CDQP, ADQM nên khẳng định D sai.
Đáp án B.
Cho các hình vẽ sau. Hình nào có dạng hình lăng trụ đứng?

Hình 1 và Hình 2.
Hình 2 và Hình 3.
Hình 3.
Tất cả các hình trên.
Đáp án : D
Dựa vào kiến thức về hình lăng trụ đứng.
Hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác.
Cả 3 hình đều là hình lăng trụ đứng, trong đó Hình 1 và Hình 2 là hình lăng trụ đứng tứ giác (hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác); Hình 3 là hình lăng trụ đứng tam giác.
Đáp án D.
Diện tích xung quanh của hình hộp chữ nhật có độ dài hai đáy là 6cm;8cm và chiều cao 10cm là:
6.8.10(cm2).
(6+8).10(cm2).
6+8+10(cm2).
2.(6+8).10(cm2).
Đáp án : D
Sử dụng công thức tính diện tích xung quanh của hình hộp chữ nhật:
Sxq = Cđáy . h
Diện tích xung quanh của hình hộp chữ nhật là:
Sxq=2(6+8).10(cm2).
Đáp án D.
Cho lăng trụ đứng tam giác ABC.DEF. Các mặt bên của lăng trụ là
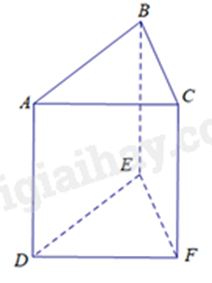
ABC;DEF.
ABC;DEF;ACFD.
ABED;BCFE.
ABED;BCFE;ACFD.
Đáp án : D
Dựa vào kiến thức về hình lăng trụ tam giác.
Các mặt bên của lăng trụ là: ABED, BCFE, ACFD.
Đáp án D.
Cho hình lăng trụ đứng có chu vi đáy, diện tích đáy và chiều cao lần lượt là C,S,h. Khẳng định đúng là
Sxq=C.h.
V=C.S.
V=C.h.
Sxq=Vh.
Đáp án : A
Dựa vào công thức tính diện tích xung quanh và thể tích của hình lăng trụ.
Công thức tính diện tích xung quanh của hình lăng trụ đứng là: Sxq=C.h.
Thể tích của hình lăng trụ đứng là: V=S.h.
Vậy đáp án đúng là A.
Đáp án A.
Cho hình vẽ sau. Góc kề bù với góc xOy là:
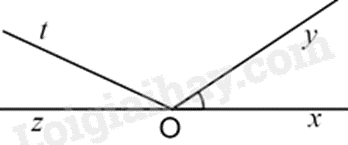
^zOy.
^tOy.
^tOz.
^xOt.
Đáp án : A
Dựa vào kiến thức về hai góc kề bù.
Góc kề bù với góc xOy là ^zOy.
Đáp án A.
Góc COD có số đo bằng bao nhiêu độ?
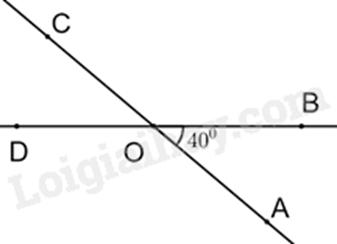
140∘.
90∘.
50∘.
40∘.
Đáp án : D
Dựa vào kiến thức về hai góc đối đỉnh: hai góc đối đỉnh thì bằng nhau.
Vì ^COD và ^AOB là hai góc đối đỉnh nên ^COD=^AOB=40∘.
Đáp án D.
Thực hiện phép tính (tính hợp lý nếu có thể):
a) 73+−812+54.
b) (−23)2.674+−74.(−23)2.
c) (623−633)−(2733−1723)+247.
Dựa vào quy tắc tính với số hữu tỉ, lũy thừa với số mũ tự nhiên.
a) 73+−812+54
= 2812+−812+1512
= 3512.
b) (−23)2.674+−74.(−23)2
=(−23)2.(674+−74)
=49.604=609=203.
c) (623−633)−(2733−1723)+247
=623−633−2733+1723+247
=(623+1723)+(−633+−2733)+247
=1+(−1)+247=247
Tìm x, biết:
a) 67−x=1228.
b) −53+710x=0,2.
c) (2x+6)2=8125.
a), b) Chuyển vế để tìm x.
c) Với A2=B2, ta chia hai trường hợp: TH1: A = B; TH2: A = - B.
a) 67−x=1228
x=67−1228
x=2428−1228
x=1228=37
Vậy x=37
b) −53+710x=0,2
710x=15+53
710x=315+2515=2815
x=2815:710
x=83
Vậy x=83
c) (2x+6)2=8125
(2x+6)2=(95)2=(−95)2.
* TH1: 2x+6=95
2x=95−6
2x=−215
x=−215:2
x=−2110.
* TH2: 2x+6=−95
2x=−95−6
2x=−395
x=−395:2
x=−3910.
Vậy x∈{−3910;−2110}.
Cho hình vẽ bên.
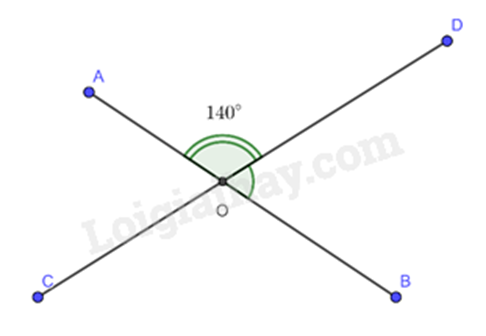
Tính ^DOB biết ^AOD=140∘.
Sử dụng kiến thức hai góc kề bù: Hai góc kề bù thì tổng của chúng bằng 180∘.
Vì ^AOD và ^DOB là 2 góc kề bù nên ^AOD+^DOB=180∘
140∘+^DOB=180∘
^DOB=180∘−140∘
^DOB=40∘.
Vậy ^DOB=40∘.
Thùng của một xe rùa điện có dạng hình lăng trụ đứng tứ giác; mặt đáy của hình lăng trụ này là một hình thang vuông có độ dài đáy lớn, đáy nhỏ và chiều cao lần lượt là 0,9m; 0,6m và 0,5m, chiều cao của hình lăng trụ là 0,6m (xem hình vẽ bên dưới). Để đảm bảo an toàn cho bác công nhân chở cát, mỗi chuyến xe chỉ vận chuyển được 96% thể tích của thùng xe. Hỏi bác công nhân phải vận chuyển ít nhất bao nhiêu chuyến xe để chở hết 54m3 cát?
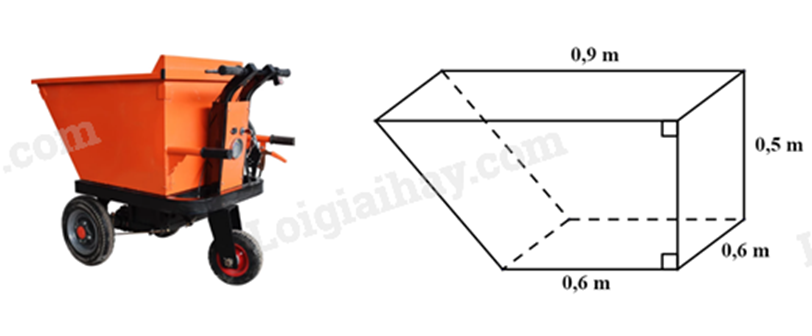
Sử dụng công thức tính thể tích hình lăng trụ đứng tứ giác.
Tính thể tích cát của mỗi chuyến xe.
Từ đó tính số chuyến xe ít nhất để vận chuyển hết cát.
Thể tích của thùng xe là:
(0,9+0,6).0,52.0,6=0,225(m3)
Thể tích cát của mỗi chuyến xe là:
0,225.96%=0,216(m3)
Ta có: 54:0,216=250.
Vậy cần ít nhất 250 chuyến xe để có thể vận chuyển hết 54m3 cát.
Một cửa hàng điện tử nhập về lô hàng gồm 50 chiếc điện thoại, giá tiền của một chiếc điện thoại khi nhập về là 10 000 000 đồng. Sau khi đã bán được 40 chiếc điện thoại với giá bằng 120%giá vốn mua ban đầu thì lượng khách hàng mua sản phẩm giảm xuống nên cửa hàng đã thực hiện chương trình giảm giá đặc biệt dành cho 10 chiếc điện thoại cuối cùng để thu hút khách hàng. Hỏi sau khi bán hết lô hàng trên, cửa hàng kỳ vọng lãi được 70 000 000 đồng thì phải giảm giá bao nhiêu phần trăm cho 10 chiếc điện thoại cuối cùng so với giá bán 40 chiếc điện thoại trước đó.
Tính giá vốn của 50 chiếc điện thoại.
Tính số tiền bán được của 40 chiếc điện thoại.
Tính giá tiền của một chiếc điện thoại khi bán với giá bằng 120%giá vốn.
Tính số tiền còn thiếu để được lãi 70000000 đồng từ lô hàng trên.
Tính giá tiền của một chiếc điện thoại sau khi giảm giá.
Tính phần trăm giá tiền của chiếc điện thoại sau khi giá so với giá bán trước đó.
Giá vốn của 50 chiếc điện thoại là:
50.10000000=500000000 (đồng)
Số tiền bán được của 40 chiếc điện thoại là:
40.10000000.120%=480000000 (đồng)
Giá tiền của một chiếc điện thoại khi bán với giá bằng 120% giá vốn là:
10000000.120%=12000000 (đồng)
Số tiền còn thiếu để được lãi 70000000 đồng từ lô hàng trên là:
500000000+70000000−480000000=90000000 (đồng)
Giá tiền của một chiếc điện thoại sau khi giảm giá là:
90000000:10=9000000 (đồng)
Phần trăm giá tiền của chiếc điện thoại sau khi giá so với giá bán trước đó là:
900000012000000=0,75=75%
Vậy để lãi được 70000000 đồng từ lô hàng trên thì cửa hàng đã giảm 100%−75%=25% so với giá bán trước đó.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365