Đề số 3 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán

Câu 5 (TH): Cho hàm số $y = {x^4} - 2{x^2} - 1$ có đồ thị $\left( C \right)$ . Số tiếp tuyến song song với trục hoành của đồ thị $\left( C \right)$ là

A. $1$ B. $2$

C. $3$ D. $0$

Câu 6 (VD): Hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật. Tam giác $SAB$ là tam giác đều cạnh $a.$ Mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng $SA$ và $BC$ bằng:

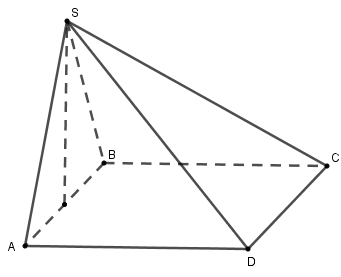
A. $a$ B. $\frac{a}{2}$

C. $\frac{{a\sqrt 3 }}{2}$ D. $\frac{{a\sqrt 3 }}{4}$

Câu 7 (VD): Nếu $f\left( x \right) = x\sin x$ thì $f'\left( {\frac{{7\pi }}{2}} \right)$ bằng

A. $- 1$ B. $\frac{{7\pi }}{2}$

C. $1$ D. $7\pi$

Câu 8 (TH): Giới hạn $\mathop {\lim }\limits_{x \to 2018} \frac{{{x^2} - 2019x + 2018}}{{x - 2018}}$ bằng

A. $2020$ B. $2017$

C. $2019$ D. $2018$

Câu 9 (TH): Đạo hàm của hàm số $y = \sqrt {\sin x + 2}$ bằng

A. $y' = \frac{{\cos x}}{{\sqrt {\sin x + 2} }}$

B. $y' = - \frac{{\cos x}}{{2\sqrt {\sin x + 2} }}$

C. $y' = \frac{1}{{2\sqrt {\sin x + 2} }}$

D. $y' = \frac{{\cos x}}{{2\sqrt {\sin x + 2} }}$

Câu 10 (VD): Giới hạn $\mathop {\lim }\limits_{x \to 0} \frac{{\cos 2018x - \cos 2019x}}{x}$ bằng

A. $0$ B. $+ \infty$

C. $- \infty$ D. $\frac{{4037}}{2}$

Câu 11 (VD): Giả sử $M$ là điểm có hoành độ ${x_0} = 1$ thuộc đồ thị hàm số $\left( C \right)$ của hàm số $y = {x^3} - 6{x^2} + 1$ . Khẳng định nào dưới đây đúng?

A. Tiếp tuyến của đồ thị $\left( C \right)$ tại $M$ có hệ số góc dương.

B. Góc giữa tiếp tuyến tại $M$ và trục hoành bằng ${60^0}$ .

C. Đồ thị $\left( C \right)$ không có tiếp tuyến tại $M$ .

D. Tiếp tuyến của đồ thị $\left( C \right)$ tại $M$ vuông góc với đường thẳng $\left( d \right):x - 9y = 0$ .

Câu 12 (TH): Với $a$ và $b$ là hai đường thẳng chéo nhau tùy ý, mệnh đề nào sau đây sai?

A. Tồn tại duy nhất một mặt phẳng $\left( P \right)$ chứa $b$ sao cho $a \bot \left( P \right)$

B. $a$ và $b$ là hai đường thẳng phân biệt

C. Tồn tại duy nhất một mặt phẳng $\left( P \right)$ chứa $b$ sao cho $a//\left( P \right)$

D. Nếu $\Delta$ là đường thẳng vuông góc chung của $a$ và $b$ thì $\Delta$ cắt cả hai đường thẳng $a$ và $b.$

Câu 13 (VD): Cho hàm số $f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {x + 3} - 2}}{{{x^2} - 1}},x > 1\\ax + 2,\,\,\,\,\,\,\,\,\,\,\,x \le 1\end{array} \right.$ . Giá trị của $a$ để hàm số liên tục tại $x = 1$ là

A. $a = - \frac{{17}}{8}$ B. $a = \frac{{15}}{8}$

C. $a = - \frac{{15}}{8}$ D. $a = \frac{{17}}{8}$

Câu 14 (VD): Cho hình chóp $S.ABC,D$ là trung điểm của đoạn $SA.$ Gọi ${h_1};{h_2}$ lần lượt là khoảng cách từ $S$ và $D$ đến mặt phẳng $\left( {ABC} \right).$ Tỉ số $\frac{{{h_1}}}{{{h_2}}}$ bằng

A. $\frac{1}{3}$ B. $3$ C. $2$ D. $\frac{1}{2}$

Câu 15 (VD): Hình chóp đều $S.ABCD$ có $SA = AB = a$ . Cosin góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAD} \right)$ bằng

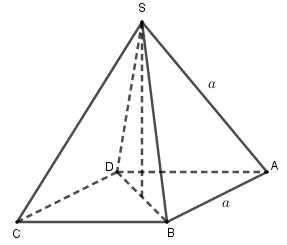
A. $\frac{{\sqrt 2 }}{2}$ B. $- \frac{{\sqrt 2 }}{2}$

C. $\frac{1}{3}$ D. $- \frac{1}{3}$

Câu 16 (VD): Cho hàm số $f\left( x \right) = \frac{1}{{{x^2} + 1}}$ . Tập nghiệm của bất phương trình $f'\left( x \right) > 0$ là

A. $\mathbb{R}$ B. $\emptyset$

C. $\left( { - \infty ;0} \right)$ D. $\left( {0; + \infty } \right)$

Câu 17 (VD): Cho hình lập phương $ABCD.A'B'C'D'$ có cạnh bằng $a$ . $M,N,P,Q$ lần lượt là trung điểm của $AB,BC,C'D'$ và $D'A'$ . Khoảng cách giữa hai đường thẳng $MN$ và $PQ$ bằng

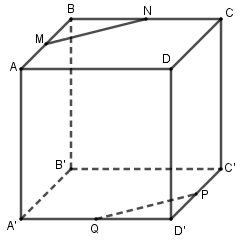
A. $a$ B. $\frac{{a\sqrt 2 }}{2}$

C. $\frac{{a\sqrt 6 }}{2}$ D. $a\sqrt 2$

Câu 18 (TH): Đạo hàm của hàm số $y = \sin \left( {{x^3}} \right)$ là

A. $y' = 3{x^2}\sin \left( {{x^3}} \right)$

B. $y' = 3{x^2}\cos \left( {{x^3}} \right)$

C. $y' = 3\cos \left( {{x^2}} \right)$

D. $y' = 3{x^2}\cos \left( {{x^2}} \right)$

Câu 19 (VD): Giới hạn $\lim \frac{{{{12}^n} - {{11}^n}}}{{{4^n} + {{4.12}^n} + 3}}$ bằng

A. $\frac{1}{{12}}$ B. $\frac{1}{4}$

C. $+ \infty$ D. $0$

Câu 20 (TH): Trong không gian cho hai đường thẳng $a,b$ và mặt phẳng $\left( P \right).$ Mệnh đề nào sau đây đúng?

A. Nếu $a$ và $b$ phân biệt, cùng song song với $\left( P \right)$ thì $a$ và $b$ song song với nhau

B. Nếu $b$ song song với $\left( P \right)$ và $a$ vuông góc với $\left( P \right)$ thì $a$ vuông góc với $b$

C. Nếu $a$ và $b$ cùng vuông góc với $\left( P \right)$ thì $a$ và $b$ song song với nhau

D. Nếu $b$ và $\left( P \right)$ cùng vuông góc với $a$ thì $b$ song song với $\left( P \right)$

PHẦN II: TỰ LUẬN (5 điểm)

Câu 21 (VD) (1 điểm): Cho hàm số $y = f\left( x \right) = 2x + \sqrt {3 - {x^2}} .$ Giải phương trình $f'\left( x \right) = 0.$

Câu 22 (VD) (1,5 điểm): Cho hàm số $y = f\left( x \right) = - {x^4} - {x^2} + 6$ . Viết phương trình tiếp tuyến của đồ thị hàm số biết rằng tiếp tuyến vuông góc với đường thẳng $d:y = \frac{1}{6}x - 1.$

Câu 23 (VD) (2,5 điểm): Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $SA$ vuông góc với mặt phẳng đáy và $AB = \sqrt 3 a,AD = a,SA = a$ .

a) Chứng minh tam giác $SDC$ vuông.

b) Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ .

c) Tính theo $a$ khoảng cách từ điểm $C$ đến mặt phẳng $\left( {SBD} \right)$ .