Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 1 Toán 7 Cánh diều
Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 13
Đề cương ôn tập học kì 1 Toán 7 - Cánh diều Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 12 Đề thi giữa kì 1 Toán 7 Cánh diều - Đề số 11 Đề thi giữa kì 1 Toán 7 - Đề số 10 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 9 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 8 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 7 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 6 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 5 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 4 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 3 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 2 - Cánh diều Đề thi giữa kì 1 Toán 7 - Đề số 1 - Cánh diềuĐề thi giữa kì 1 Toán 7 Cánh diều - Đề số 13
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Khẳng định nào sau đây đúng?
5∈Q.
−32∈Z.
−1,5∈N.
−32∉Q.
Đáp án : A
Dựa vào kiến thức về các tập hợp.
5=51 nên 5∈Q.
−32=−1,5 không phải số nguyên nên −32∉Z.
−1,5<0 nên −1,5∉N.
−32 là số hữu tỉ nên −32∈Q.
Vậy khẳng định A đúng, khẳng định B, C, D sai.
Đáp án A.
Số đối của 47 là:
74.
−4−7.
−47.
−74.
Đáp án : C
Số đối của số hữu tỉ a là – a.
Số đối của 47 là −47.
Đáp án C.
Trong các số −4,5;−213;−4−5;0;−47;2423 có bao nhiêu số hữu tỉ âm?
1.
2.
3.
4.
Đáp án : C
Số hữu tỉ âm là các số hữu tỉ nhỏ hơn 0.
Ta có: −4,5=−4510;−213=−73;−4−5=45
Vậy có 3 số hữu tỉ âm, đó là: −4,5;−213;−47.
Đáp án C.
Khẳng định nào sau đây sai?

Điểm A biểu diễn số hữu tỉ −32.
Điểm B biểu diễn số hữu tỉ −13.
Điểm C biểu diễn số hữu tỉ 12.
Điểm D biểu diễn số hữu tỉ 43.
Đáp án : A
Xác định 1 đơn vị của trục số, từ đó xác định số hữu tỉ tương ứng với các điểm.
Vì -1 cách 0 là 6 đơn vị nên 1 đơn vị tương ứng với: 1:6=16.
Điểm A cách 0 là 7 đơn vị về phía bên trái nên điểm A biểu diễn số hữu tỉ −76. (Khẳng định A sai).
Điểm B cách 0 là 2 đơn vị về phía bên trái nên điểm B biểu diễn số hữu tỉ −26=−13. (Khẳng định B đúng).
Điểm C cách 0 là 3 đơn vị về bên phải nên điểm C biểu diễn số hữu tỉ 36=12. (Khẳng định C đúng).
Điểm D cách 0 là 8 đơn vị về bên phải nên điểm D biểu diễn số hữu tỉ 86=43. (Khẳng định D đúng).
Vậy chọn đáp án A.
Đáp án A.
Kết quả của phép tính (−12)3 là:
−16.
−18.
−1−8.
18.
Đáp án : B
Sử dụng kiến thức về lũy thừa (ab)n=anbn.
Ta có: (−12)3=(−1)323=−18
Đáp án B.
Với a,b,c là ba số hữu tỉ bất kì, nếu a−b=c thì:
a=b+c.
a=−b−c.
a=b−c.
a=−b+c.
Đáp án : A
Sử dụng quy tắc chuyển vế.
Nếu a−b=c thì a=b+c.
Đáp án A.
Các mặt của hình lập phương đều là:
Hình vuông.
Tam giác đều.
Hình chữ nhật.
Hình thoi.
Đáp án : A
Dựa vào kiến thức về hình lập phương.
Hình lập phương có 6 mặt bằng nhau và đều là hình vuông.
Đáp án A.
Cho hình lập phương ABCD.EFGH như hình vẽ, có cạnh bằng 4cm. Thể tích của hình lập phương đó là:
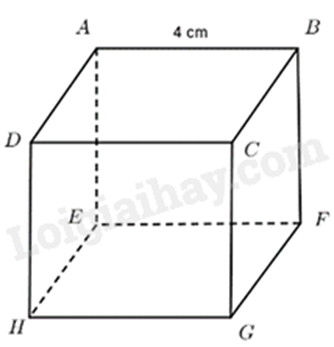
64cm3.
96cm3.
16cm3.
64cm2.
Đáp án : A
Sử dụng công thức tính thể tích của hình lập phương: V=a3 (a là độ dài cạnh)
Thể tích của hình lập phương là: V=43=64(cm3).
Đáp án A.
Hình hộp chữ nhật ABCD.A′B′C′D′ có AB=5cm; AA’ = 3cm. Khẳng định nào sau đây đúng?
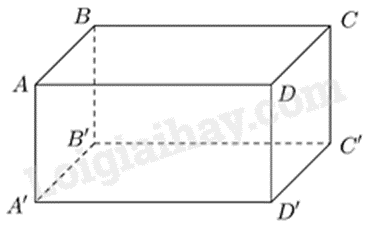
DC=3cm.
BB′=5cm.
D′C′=5cm.
A′D′=5cm.
Đáp án : C
Hình hộp chữ nhật có các cạnh đối bằng nhau.
Cạnh D′C′=DC=AB=5cm.
Cạnh BB′=AA′=3cm.
Cạnh A′D′ chưa đủ điều kiện để xác định.
Vậy đáp án đúng là C.
Đáp án C.
Cho hình lăng trụ tam giác sau. Chiều cao của hình lăng trụ sẽ là?
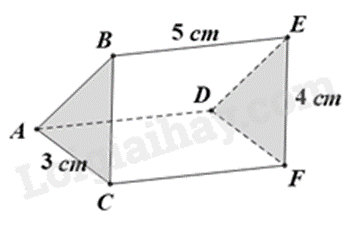
3cm.
4cm.
5cm.
7cm.
Đáp án : C
Dựa vào kiến thức về hình lăng trụ đứng tam giác.
Hình lăng trụ có hai đáy là ABC, DEF, chiều cao là BE = 5cm.
Đáp án C.
Cho đường thẳng xx’, yy’ cắt nhau tại O và ^xOy=45∘. Số đo ^x′Oy′ bằng
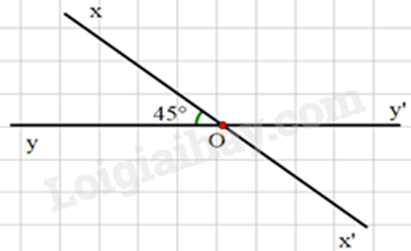
45∘.
90∘.
180∘.
135∘.
Đáp án : A
Dựa vào kiến thức về hai góc đối đỉnh.
Vì đường thẳng xx’, yy’ cắt nhau tại O nên ^xOy và ^x′Oy′ là hai góc đối đỉnh, suy ra ^x′Oy′=^xOy=45∘.
Đáp án A.
Cho hình bên. Góc kề bù với ^xAB là:
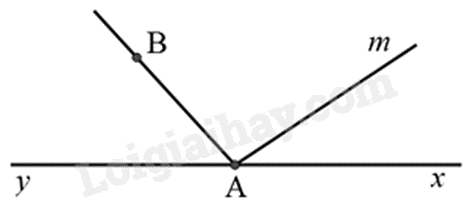
^yAB.
^yAm.
^mAB.
^xAm.
Đáp án : A
Hai góc kề bù là hai góc vừa kề, vừa bù nhau.
Góc kề bù với ^xAB là ^yAB.
Đáp án A.
Thực hiện phép tính (tính hợp lí nếu có thể):
a) 49+59.−310
b) 925.−2311+111.(35)2
c) 83+44−2725.26
Sử dụng các quy tắc tính với số hữu tỉ và lũy thừa với số mũ tự nhiên.
a) 49+59.−310
=49+−16=818+−318=518
b) 925.−2311+111.(35)2
=925.−2311+111.925
=925.(−2311+111)
=925.(−2)
=−1825
c) 83+44−2725.26
=(23)3+(22)4−2752.26=29+28−2752.26
=27.(22+2−1)52.26
=27.552.26=25
Tìm x, biết:
a) x−32=−45
b) 57x+58=−0,375
Sử dụng quy tắc chuyển vế.
a) x−32=−45
x=−45+32x=−810+1510x=710
Vậy x=710.
b) 57x+58=−0,375
57x+58=−3857x=−38−5857x=−1x=−1:57x=−75
Vậy x=−75.
Quan sát hình bên, tính số đo góc xOy và số đo góc yOx’.
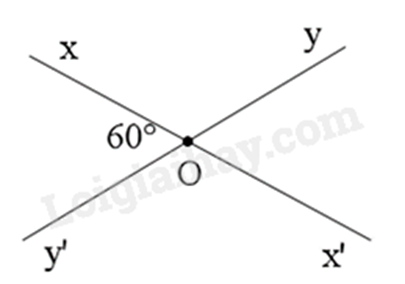
Sử dụng kiến thức về hai góc đối đỉnh và hai góc kề bù.
Vì xx’ cắt yy’ tại O nên ^yOx′=^xOy′=60∘ (hai góc đối đỉnh).
Vì ^xOy và ^xOy′ là hai góc kề bù nên ^xOy+^xOy′=180∘
suy ra ^xOy=180∘−^xOy′=180∘−60∘=120∘.
Tính diện tích xung quanh và thể tích của hình lăng trụ ABC.DEF?
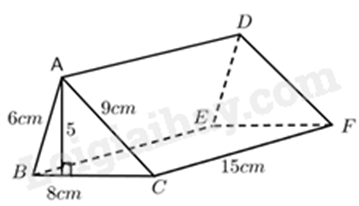
Sử dụng công thức tính diện tích xung quanh và thể tích hình lăng trụ:
Sxq = Cđáy.chiều cao.
V = Sđáy.chiều cao.
Tính diện tích xung quanh của hình lăng trụ ABC.DEF là:
Sxq=(6+9+8).15=345(cm2)
Thể tích của hình lăng trụ ABC.DEF là:
V=(5.8):2.15=300(cm3)
Lưới chắn bóng sân đá góp phần quan trọng vào việc bảo vệ sự an toàn cho các sân bóng cỏ nhân tạo. Vì vậy cần phải mắc hệ thống lưới bao quanh sân bóng đá. Có thể là lưới sợi dù, sợi nilon hay sợi nhựa, được gắn cố định vào cọc bê tông, gỗ hay cọc sắt. Một sân bóng đá mini ở phường Hiệp Bình Chánh có dạng hình chữ nhật (xem hình bên) có kích thước chiều dài 50m, chiều rộng 30m. Chủ sân cần mua lưới chắn sân với chiều cao lưới là 8m để bao quanh sân bóng.

a) Tính diện tích lưới cần mua?
b) Nếu mỗi mét vuông lưới có giá 20 000 đồng thì chủ sân cần trả bao nhiêu tiền để mua đủ lưới bao quanh sân bóng?
a) Diện tích lưới cần mua chính là diện tích xung quanh của hình hộp chữ nhật.
Sxq = Cđáy.chiều cao.
b) Số tiền mua lưới = Diện tích lưới . 20 000.
a) Diện tích lưới cần mua là:
Sxq=(50+30).2.8=1280(m2)
b) Số tiền mua lưới là:
1280.20000=25600000 (đồng)
Anh Nam làm việc 8 giờ một ngày thì nhận được mức lương cơ bản cho một ngày là 320000 đồng. Tháng 11, anh Nam làm việc trong 26 ngày. Để kiếm thêm thu nhập, anh Nam có thể làm tăng ca. Biết rằng một ngày được tăng ca tối đa 3 giờ và tiền lương tăng ca một giờ bằng 150% tiền lương cơ bản một giờ. Hỏi tháng 11, anh Nam phải làm tăng ca ít nhất bao nhiêu ngày để có tổng tiền lương là 10300000 đồng?
Tính số tiền tăng ca mỗi ngày trong 3 giờ của anh Nam
= số tiền 1 ngày : 8 tiếng . 150% . 3 tiếng
Tính số tiền tăng ca mà anh Nam nhận được trong tháng 11
= tổng số tiền nhận được - số tiền lương cơ bản. số ngày công
Số ngày tăng ca = tổng số tiền tăng ca : số tiền tăng ca mỗi ngày
Làm tăng ca một ngày trong 3 giờ thì anh Nam nhận thêm được số tiền là:
320000:8.150%.3=180000 (đồng)
Số tiền tăng ca mà anh Nam nhận được trong tháng 11 là:
10300000−320000.26=1980000 (đồng)
Anh Nam phải làm tăng ca ít nhất số ngày là:
1980000:180000=11 (ngày).
Vậy anh Nam phải tăng ca ít nhất 11 ngày để có tổng tiền lương là 10300000 đồng.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365