Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi giữa kì 1 Toán 7 Kết nối tri thức
Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 13
Đề cương ôn tập học kì 1 Toán 7 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 12 Đề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 11 Đề thi giữa kì 1 Toán 7 - Đề số 10 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 9 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 8 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 7 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 6 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 5 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 4 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 3 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 2 - Kết nối tri thức Đề thi giữa kì 1 Toán 7 - Đề số 1 - Kết nối tri thứcĐề thi giữa kì 1 Toán 7 Kết nối tri thức - Đề số 13
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Khẳng định nào sau đây sai?
−5∈Q.
−35∉Z.
6,7∈N.
34∈Q.
Đáp án : C
Dựa vào kiến thức về các tập hợp N,Z,R,Q.
−5=−51 là số hữu tỉ nên −5∈Q là khẳng định đúng.
−35 không phải số nguyên nên −35∉Z là khẳng định đúng.
6,7 không phải số tự nhiên nên khẳng định 6,7∈N là khẳng định sai.
34 là số hữu tỉ nên 34∈Q là khẳng định đúng.
Đáp án C.
Số đối của −12 là
−12 .
-1.
1.
12.
Đáp án : D
Số đối của số hữu tỉ a là – a.
Số đối của −12 là: −(−12)=12.
Đáp án D.
Số 125 viết được dưới dạng luỹ thừa của 5 là
5125.
-5125.
-53.
53.
Đáp án : D
Biểu diễn 125 thành lũy thừa của 5.
Ta có: 125=5.5.5=53.
Đáp án D.
Viết số (19)4 dưới dạng luỹ thừa cơ số 13 ta được
(13)4.
(13)8.
(13)6.
(13)12.
Đáp án : B
Dựa vào kiến thức lũy thừa của lũy thừa: (xm)n=xm.n.
Ta có: (19)4=[(13)2]4=(13)2.4=(13)8.
Đáp án B.
Cho x∈Q,x≠0 và x3.x2 bằng:
x6.
x7:x2.
x3+x2.
(x3)2.
Đáp án : B
Dựa vào kiến thức:
xm.xn=xm+nxm:xn=xm−n(x≠0;m≥n)
(xm)n=xm.n
Ta có: x3.x2=x3+2=x5.
x7:x2=x7−2=x5.
(x3)2=x3.2=x6.
Do đó x3.x2=x7:x2.
Đáp án B.
Kết quả của phép tính √16.√4−√25+2√49 là
15.
17.
-17.
16.
Đáp án : B
Sử dụng kiến thức về căn bậc hai và thực hiện phép tính.
Ta có:
√16.√4−√25+2√49=4.2−5+2.7=8−5+14=17
Đáp án B.
Cho hai góc kề bù ^xOy và ^yOz, biết ^yOz=100∘. Khi đó số đo ^xOy là
100∘.
80∘.
10∘.
110∘.
Đáp án : B
Sử dụng kiến thức về hai góc kề bù: tổng hai góc kề bù bằng 180∘.
Vì ^xOy và ^yOz là hai góc kề bù nên ^xOy+^yOz=180∘.
Suy ra ^xOy=180∘−^yOz=180∘−100∘=80∘.
Đáp án B.
Cho ^xOy=70∘, tia Oz là tia phân giác của ^xOy. Số đo của ^xOz là:
30∘.
140∘.
60∘.
35∘.
Đáp án : D
Khi Oz là tia phân giác của góc xOy thì ^xOz=^zOy=12^xOy.
Vì tia Oz là tia phân giác của ^xOy nên ^xOz=^zOy=12^xOy
Suy ra ^xOz=12^xOy=12.70∘=35∘.
Đáp án D.
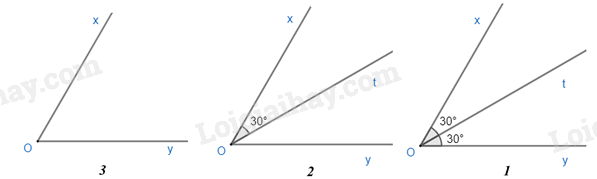
Cho ^xOy=60∘. Nêu cách dựng tia phân giác Oz của góc xOy. Hãy sắp xếp một cách hợp lý các câu sau đây để có lời giải của bài toán trên.
1. Viết ký hiệu ^xOz=^zOy.
2. Vẽ tia Oz nằm giữa hai tia Ox và Oy sao cho ^xOz=30∘.
3. Vẽ ^xOy=60∘ .
Sắp xếp nào sau đây là đúng?
3, 2, 1.
1, 2, 3.
3, 1, 2.
2, 3, 1.
Đáp án : A
Dựa vào cách dựng tia phân giác của một góc.
Thứ tự sắp xếp đúng là: 3 – 2 – 1.
3. Vẽ ^xOy=60∘ .
2. Vẽ tia Oz nằm giữa hai tia Ox và Oy sao cho ^xOz=30∘.
1. Viết ký hiệu ^xOz=^zOy.
Đáp án A.
Khẳng định đúng là:
Hai góc đối đỉnh thì bằng nhau.
Hai góc bằng nhau thì đối đỉnh.
Hai góc đối đỉnh thì bù nhau.
Hai góc có đỉnh trùng nhau là hai góc đối đỉnh.
Đáp án : A
Dựa vào tính chất của hai góc đối đỉnh.
Hai góc đối đỉnh thì bằng nhau nên đáp án A đúng.
Đáp án A.
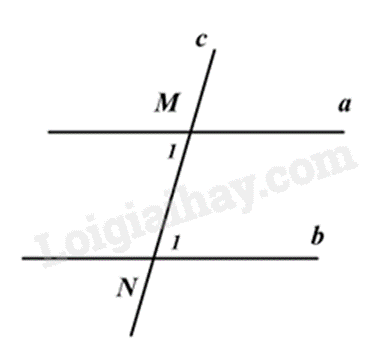
Cho hình vẽ bên. Biết a//b, ^M1=85o, khi đó ^N1=?
850.
950.
1000.
1050.
Đáp án : A
Dựa vào tính chất của hai đường thẳng song song (hai góc so le trong bằng nhau).
Vì a // b nên ^M1=^N1=85∘ (hai góc so le trong)
Đáp án A.
Trong các khẳng định sau, khẳng định nào cho ta một định lí?
Hai góc so le trong thì bằng nhau.
Hai góc bằng nhau thì so le trong.
Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
Đáp án : C
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết.
Dựa vào kiến thức về tính chất hai góc so le trong, hai đường thẳng song song.
Chỉ có hai góc so le trong của hai đường thẳng song song mới bằng nhau nên A không phải định lí.
Hai góc bằng nhau chưa chắc đã là hai góc so le trong nên B không phải định lí.
Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau nên C là định lí, D không phải định lí.
Đáp án C.
Thực hiện phép tính:
a) 237+43−97+106;
b) (58−√912):34+118:34;
c) (0,(3)+|−2|3):√254−(23+32)0.
Dựa vào các quy tắc thực hiện phép tính với số thực, lũy thừa và thứ tự thực hiện phép tính.
a) 237+43−97+106=(237−97)+(43+53)=5
b) (58−√912):34+118:34=(58−14+118).43=73
c) (0,(3)+|−2|3):√254−(23+32)0=(13+23).45−1=−15
Tìm x, biết:
a) 23−52x=−133;
b) 2.|3−2x|+12=52;
c) x2.(2x−6)−2x2=0.
a) Sử dụng quy tắc chuyển vế.
b) Chuyển vế, sử dụng kiến thức |A|=k>0 thì xảy ra hai trường hợp: A=k hoặc A=−k.
c) Sử dụng tính chất phân phối của phép nhân với phép cộng.
Khi A.B = 0 thì A = 0 hoặc B = 0.
a) 23−52x=−133
52x=23+133x=2
Vậy x=2.
b) 2|3−2x|+12=52
|3−2x|=1
TH1: 3−2x=1
2x=3−12x=2x=2:2x=1
TH2: 3−2x=−1
2x=3−(−1)2x=4x=4:2x=2
Vậy x=1;x=2.
c) x2.(2x−6)−2x2=0
x2.(2x−6−2)=0x2.(2x−8)=0
TH1: x2=0
x=0
TH2: 2x−8=0
2x=82x=23x=3
Vậy x=0;x=3.
Một ngày cửa hàng bánh mì nhập 200 chiếc bánh mì để bán. Buổi sáng, cửa hàng bán được 35 số bánh mì với giá 15000đồng một cái.
a) Số tiền buổi sáng cửa hàng bánh mì thu được là bao nhiêu?
b) Buổi chiều, để bán nốt số bánh mì còn lại cửa hàng giảm giá 20% so với giá bán buổi sáng. Tính tổng số tiền bán bánh mì của cửa hàng thu được trong một ngày nếu bán hết bánh mì.
a) Tính số bánh mì buổi sáng bán được = 35 . tổng số bánh.
Tính số tiền buổi sáng bán được = giá một chiếc . số bánh bán được.
b) Tính giá bánh mì sau khi giảm 20% = giá một chiếc . (100% - 20%).
Tính số bánh mì còn lại sau buổi sáng = tổng số bánh – số bánh đã bán.
Tính số tiền bán được vào buổi chiều = số bánh còn lại . giá sau khi giảm.
Tính tổng số tiền bán bánh mì.
a) Buổi sáng bán được số bánh mì là:
200.35=120(bánh mì)
Số tiền buổi sáng cửa hàng bánh mì thu được là:
15000.120=1800000(đồng)
b) Giá bán bánh mì sau khi giảm 20% là:
15000.(100%−20%)=12000(đồng)
Số bánh mì còn lại sau buổi sáng là:
200−120=80(bánh mì)
Số tiền thu được khi bán nốt bánh mì còn lại sau buổi sáng là:
12000.80=960000 (đồng)
Tổng số tiền bán bánh mì của cửa hàng thu được trong một ngày là:
1800000+960000=2760000 (đồng)
Vậy tổng số tiền bán bánh mì của cửa hàng thu được trong một ngày là 2 760 000 đồng.
Cho hình vẽ bên, biết ^FDC=135∘,^CBx=45∘,^DCz=135∘, Dy∥Bx,Dy⊥BF tại điểm F.
a) Vẽ hình và chứng minh Cz∥Dy.
b) Chứng minh BC là tia phân giác của ^FBx.
c) Kẻ tia Ct là tia phân giác của ^BCD. Chứng minh Ct∥Dy.

a) Sử dụng dấu hiệu nhận biết hai đường thẳng song song (hai góc so le trong bằng nhau)
b) Chứng minh ^FBx=90∘.
Chứng minh BC chia góc ^FBx thành hai góc bằng nhau.
c) Kéo dài Oz về phía O, ta được đường thẳng zz’ đi qua O.
Tính được ^BCD=90∘.
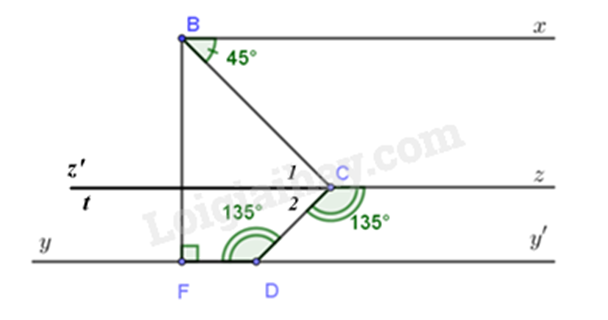
a) Vẽ lại hình
Vì ^FDC=^DCz=135∘ mà ^FDC và ^DCz ở vị trí so le trong nên Cz∥Dy (dấu hiệu nhận biết)
b) Ta có, Dy//Bx;By⊥Dy suy ra BF⊥Bx (tính chất)
Suy ra ^FBx=90∘
Tia BC nằm trong ^FBx
Mà ^CBx=12^FBx=45∘
Suy raBC là tia phân giác của ^FBx.
c) Kéo dài Oz về phía O, ta được đường thẳng zz’ đi qua O.
Khi đó Bx//zz′//yy′
Suy ra ^xBC=^C1;^C2=^CDy′ (1).
Vì ^yDC+^CDy′=180∘ (hai góc kề bù) nên ^CDy′=180∘−^yDC=180∘−135∘=45∘ (2).
Từ (1) và (2) suy ra ^C1=45∘;^C2=45∘
Do đó ^BCD=^C1+^C2=45∘+45∘=90∘
Vì Ct là tia phân giác của ^BCD nên ^DCt=12^BCD=45∘ (tính chất)
Suy ra ^DCt=^CDy′=45∘.
Mà ^DCt và ^CDy′ là hai góc so le trong.
Do đó Ct∥Dy (dấu hiệu nhận biết)
Tìm x,y,z biết: √(x−2024)2+|x+y−4z|+y2.√5=0 với x,y,z∈R.
Dựa vào tính chất của giá trị tuyệt đối, bình phương của một số.
Vì y2≥0 với mọi y∈R và √5>0 nên y2.√5≥0 với mọi y∈R .
Ta có: √(x−2024)2=|x−2024|≥0 với mọi x∈R;
|x+y−4z|≥0 với mọi x,y,z∈R và y2.√5≥0 với mọi y∈R
nên √(x−2024)2+|x+y−4z|+y2.√5≥0 với mọi x,y,z∈R.
Theo đề bài, ta có √(x−2024)2+|x+y−4z|+y2.√5=0 hay |x−2024|+|x+y−4z|+y2.√5=0.
Giá trị của biểu thức bằng 0 khi
|x−2024|=0|x+y−4z|=0y2.√5=0
Với |x−2024|=0 thì x−2024=0, suy ra x=2024;
Với y2.√5=0 (do √5≠0) nên y2=0, suy ra y=0.
Thay x=2024; y=0 vào |x+y−4z|=0 hay x+y−4z=0, ta được
2024+0−4z=0 suy ra 4z=2024, do đó z=2024:4=506.
Vậy x=2024;y=0;z=506.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365