Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 1 Toán 7 Cánh diều
Đề thi học kì 1 Toán 7 - Đề số 6 - Cánh diều
Đề thi học kì 1 Toán 7 - Đề số 7 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 8 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 9 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 10 - Cánh diều Đề thi học kì 1 Toán 7 Cánh diều - Đề số 11 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 12 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 13 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 14 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 15 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 16 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 17 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 18 Đề thi học kì 1 Toán 7 - Đề số 5 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 4 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 3 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 2 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều Đề cương ôn tập học kì 1 Toán 7 - Cánh diềuĐề thi học kì 1 Toán 7 - Đề số 6 - Cánh diều
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (3 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ −0,125?−0,125?
A. 1818
B. −18−18
C. −1125−1125
D. 11251125
Câu 2: Kết quả của phép tính: (−0,08)4.104(−0,08)4.104 là:
A. 0,840,84
B. 8484
C. 10.8410.84
D. 0,0840,084
Câu 3: So sánh 2+√372+√37 và 6+√26+√2?
A. 2+√37>6+√22+√37>6+√2
B. 2+√37<6+√22+√37<6+√2
C. 2+√37=6+√22+√37=6+√2
D. Không có đáp án
Câu 4: Sắp xếp các số |−3|;√6;|−226|;√1282;−73|−3|;√6;∣∣∣−226∣∣∣;√1282;−73 theo thứ tự tăng dần.
A. −73;|−226|;√6;|−3|;√1282−73;∣∣∣−226∣∣∣;√6;|−3|;√1282
B. −73;√6;|−3|;|−226|;√1282−73;√6;|−3|;∣∣∣−226∣∣∣;√1282
C. √1282;|−3|;|−226|;√6;−73√1282;|−3|;∣∣∣−226∣∣∣;√6;−73
D. −73;√6;|−226|;√1282;|−3|−73;√6;∣∣∣−226∣∣∣;√1282;|−3|
Câu 5: Cho góc bẹt xOyxOy. Vẽ tia OzOz nằm giữa hai tia OxOx và OyOy. Vẽ tia OmOm là phân giác của góc xOzxOz. Vẽ tia OnOn là tia phân giác của góc zOyzOy. Tính số đo góc mOn?mOn?
A. ∠mOn=300∠mOn=300
B. ∠mOn=600∠mOn=600
C. ∠mOn=900∠mOn=900
D. ∠mOn=1200∠mOn=1200
Câu 6: Cho biết xx và yy là hai đại lượng tỉ lệ nghịch, biết khi x=5x=5 thì y=10y=10. Vậy khi x=2x=2 thì yy bằng bao nhiêu?
A. 44
B. 2525
C. 11
D.5050
Câu 7: Một hình lăng trụ đứng tứ giác có độ dài cạnh bên là 20cm20cm và đáy là hình thoi với độ dài hai đường chéo là 18cm;30cm18cm;30cm. Tính thể tích của hình lăng trụ đó.
A. 6300cm36300cm3
B. 5400cm35400cm3
C. 3600cm33600cm3
D. 4800cm34800cm3
Câu 8: Trong các hình vẽ dưới đây, liệt kê tất cả các hình là hình lăng trụ đứng tam giác hoặc hình lăng trụ đứng tứ giác?
A. Tất cả 6 hình
B. Hình a), c), e), f)
C. Hình b), c), d)
D. Hình b), d)
Câu 9: Tìm xx biết 23+53x=5723+53x=57
A. 1717
B. −335−335
C. −135−135
D. 135135
Câu 10: 5m5m dây đồng nặng 43g43g. Hỏi 10km10km dây đồng như thế nặng bao nhiêu kilôgam?
A. 86kg86kg
B. 84kg84kg
C. 76kg76kg
D. 72kg72kg
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm )
Thực hiện phép tính:
a) (−34+23):511+(−14+13):511(−34+23):511+(−14+13):511
b) 2710.1625630.32152710.1625630.3215
c) |35−110|−√3625+(310)5:(310)4∣∣∣35−110∣∣∣−√3625+(310)5:(310)4
d) √144+√49−10√425√144+√49−10√425
Bài 2: (2,0 điểm)
Tìm xx, biết:
a) (−12)+(45+x)=112(−12)+(45+x)=112
b) 2x−127=32x−12x−127=32x−1
c) 5.√x−√125=05.√x−√125=0
d) |0,3−x|=13|0,3−x|=13
Bài 3: (1,5 điểm)
Hưởng ứng phong trào “Tết ấm no” để tăng thu nhập, ba tổ công nhân của một xí nghiệp đã dăng kí sản xuất tổng số 270270 sản phẩm. Biết tổ I có 1010 người, tổ II có 88 người, tổ III có 99 người và số sản phẩm của mỗi tổ sản xuất được tỉ lệ thuận với số người của tổ. Hỏi mỗi tổ đã đăng kí sản xuất bao nhiêu sản phẩm?
Bài 4: (1,5 điểm)
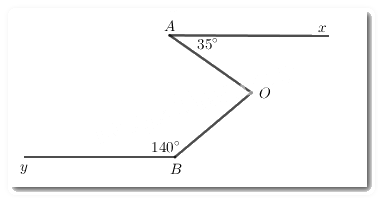
Cho hình vẽ, biết Ax//By,∠OAx=35∘,∠OBy=140∘Ax//By,∠OAx=35∘,∠OBy=140∘. Tính ∠AOB∠AOB?
Bài 5: (0,5 điểm)
Tìm số thực xx, biết: |x|+|x+2|=0|x|+|x+2|=0.
Lời giải
Phần I: Trắc nghiệm
|
1.B |
2.A |
3.A |
4.B |
5.C |
6.B |
7.A |
8.A |
9.D |
10.A |
Câu 1
Phương pháp:
Đưa số thập phân về phân số.
Cách giải:
Ta có: −0,125=−1251000=−18−0,125=−1251000=−18
Vậy phân số biểu diễn số hữu tỉ −0,125−0,125 là −18−18.
Chọn B.
Câu 2
Phương pháp:
Vận dụng công thức tính lũy thừa của một tích bằng tích các lũy thừa: (x.y)n=xn.yn(x.y)n=xn.yn
(−a)2.k=a2.k(k∈N)(−a)2.k=a2.k(k∈N)
Cách giải:
(−0,08)4.104=(−0,08.10)4=(−0,8)4=0,84(−0,08)4.104=(−0,08.10)4=(−0,8)4=0,84
Chọn A.
Câu 3
Phương pháp:
So sánh từng số hạng của tổng.
Cách giải:
Ta có: 2=√22=√4;6=√62=√362=√22=√4;6=√62=√36
Vì 4>24>2 nên √4>√2√4>√2 hay 2>√22>√2
37>3637>36 nên √37>√36√37>√36 hay √37>6√37>6
Do đó, 2+√37>6+√22+√37>6+√2
Chọn A.
Câu 4
Phương pháp:
Tính giá trị tuyệt đối của một số thực, tính căn bậc hai của một số thực.
Thực hiện so sánh các số để sắp xếp thứ tự các số.
Cách giải:
Ta có:
|−3|=−(−3)=3|−226|=−(−226)=226=113√1282=√64=√82=8
Ta có: 3=93;8=243
Vì 9<11<24 nên 93<113<243 hay 3<113<8
Mặt khác, ta có: 3=√32=√9
Vì 6<9 nên √6<√9 hay √6<3
Do đó, √6<3<113<8
Mà −73<0 nên ta có: −73<√6<3<113<8 hay −73<√6<|−3|<|−226|<√1282
Vậy thứ tự tăng dần của các số là: −73;√6;|−3|;|−226|;√1282.
Chọn B.
Câu 5
Phương pháp:
Oz là tia phân giác của góc xOy thì ta có: ∠xOz=∠zOy=∠xOy2
Cách giải:
Vì Om là tia phân giác của góc xOz nên ∠zOm=∠xOz2 hay ∠xOz=2.∠zOm
Vì On là tia phân giác của góc zOy nên ∠nOz=∠zOy2 hay ∠zOy=2.∠nOz
Vì ∠xOz và ∠zOy là hai góc kề bù nên ∠xOy+∠zOy=1800
⇒2.∠zOm+2.∠nOz=1800⇒2.(∠zOm+∠nOz)=1800⇒∠zOm+∠nOz=1800:2⇒∠zOm+∠nOz=900
Vì Oz nằm giữa hai tia Om và On nên ∠zOm+∠nOz=∠mOn=900
Vậy ∠mOn=900
Chọn C.
Câu 6
Phương pháp:
Vận dụng kiến thức về hai đại lượng tỉ lệ nghịch với nhau.
Cách giải:
x và y là hai đại lượng tỉ lệ nghịch với nhau ⇒y=ax(a≠0)
Thay x=5;y=10 vào ta được: 10=a5⇒a=10.5=50
Vậy hệ số tỉ lệ của y so với x là 50.
Ta có: y=50x, khi x=2 thì y=502=25.
Chọn B.
Câu 7
Phương pháp:
Diện tích hình thoi có độ dài hai đường chéo lần lượt là a,b được tính theo công thức: S=a.b2
Thể tích hình lăng trụ đứng tứ giác có chiều cao h và diện tích đáy S được tính theo công thức: V=S.h
Cách giải:
Diện tích đáy của hình lăng trụ đó là: S=18.302=270(cm2)
Thể tích của hình lăng trụ đó là: V=270.20=5400(cm3)
Chọn A.
Câu 8
Phương pháp:
Hình lăng trụ đứng tam giác là hình hai mặt đáy là hình tam giác song song với nhau, ba mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau.
Hình lăng trụ đứng tứ giác là hình hai mặt đáy là hình tứ giác song song với nhau, bốn mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau.
Cách giải:
Từ các hình đã cho, ta thấy:
+ Hình vẽ b), c) là hình lăng trụ đứng tứ giác.
+ Hình vẽ d) là hình lăng trụ đứng tam giác.
Vậy hình vẽ b), c) và d) là các hình lăng trụ đứng tam giác hoặc lăng trụ đứng tứ giác.
Chọn A.
Câu 9
Phương pháp:
Ta áp dụng thứ tự thực hiện phép tính để tìm x.
Cách giải:
23+53x=57
53x=57−2353x=121x=121:53x=135
Vậy x=135.
Chọn D.
Câu 10
Phương pháp:
Gọi số gam trong 10000m dây đồng là x(g)
Vì khối lượng của dây đồng tỉ lệ thuận với chiều dài của dây đồng nên lập được dãy tỉ số bằng nhau, từ đó tìm được x.
Cách giải:
Đổi 10km=10000m
Gọi số gam trong 10000m dây đồng là x(g)
Vì khối lượng của dây đồng tỉ lệ thuận với chiều dài của dây đồng nên ta có:
435=x10000
Suy ra x=435.10000=86000(g)=86(kg)
Vậy 10km dây đồng nặng 86kg
Chọn A.
Phần II. Tự luận:
Bài 1
Phương pháp:
a) Thực hiện các phép toán với các số hữu tỉ
b) Vận dụng quy tắc tính lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: (xm)n=xm.n.
Vận dụng quy tắc tính thương của hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: xm:xn=xm−n(x≠0;m≥n).
c) Vận dụng kiến thức giá trị tuyệt đối của một số thực: |x|={xkhix>0−xkhix<00khix=0
Tính toán với căn bậc hai của một số thực
Vận dụng quy tắc tính thương của hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: xm:xn=xm−n(x≠0;m≥n).
d) Tính toán với căn bậc hai của một số thực
Cách giải:
a) (−34+23):511+(−14+13):511
=(−34+23).115+(−14+13).115=(−34+23+−14+13).115=[(−34+−14)+(23+13)].115=(−44+33).115=(−1+1).115=0.115=0
b) 2710.1625630.3215
=(33)10.(24)25(2.3)30.(25)15=33.10.24.25230.330.25.15=330.2100230.330.275=2100230+75=21002105=125=132
c) |35−110|−√3625+(310)5:(310)4
=|610−110|−65+(310)5−4=|510|−65+(310)1=510−1210+310=−410=−25
d) √144+√49−10√425
=12+7−10.25=19−4=15
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ, vận dụng quy tắc chuyển vế tìm x
b) Vận dụng tính chất hai phân số bằng nhau: Nếu ab=cd thì ad=bc.
Giải [A(x)]2=a2=(−a)2
Trường hợp 1: A(x)=a
Trường hợp 2: A(x)=−a
c) Vận dụng kiến thức căn bậc hai số học của số thực, tìm x
d) |x|=a
Trường hợp a<0, khi đó phương trình không có nghiệm x
Trường hợp a>0, vận dụng kiến thức giá trị tuyệt đối của một số thực: |x|={xkhix>0−xkhix<00khix=0
Cách giải:
a) (−12)+(45+x)=112
−12+45+x=32x=32−(−12)−45x=32+12−45x=42−45x=2−45x=105−45x=65
Vậy x=65
b) 2x−127=32x−1
(2x−1)2=27.3=81(2x−1)2=(±9)2
Trường hợp 1:
2x−1=92x=10x=5
Trường hợp 2:
2x−1=−92x=−8x=−4
Vậy phương trình có nghiệm là x=5 hoặc x=−4
c) 5.√x−√125=0
5.√x−15=05.√x=15√x=15:5=15.15=125
√x=√(125)2⇒x=1625
Vậy x=1625
d) |0,3−x|=13
|310−x|=13
Trường hợp 1:
310−x=13x=310−13x=930−1030x=−130
Vậy x∈{−130;1930}
Trường hợp 2:
310−x=−13x=310−(−13)x=930+1030x=1930
Bài 3
Phương pháp:
Gọi số sản phẩm mà tổ I, tổ II, tổ III đăng kí sản xuất là z,y,z (sản phẩm) (điều kiện: z,y,z∈N)
Vận dụng bài toán tỉ lệ thuận lập được dãy tỉ số bằng nhau
Áp dụng tính chất của dãy tỉ số bằng nhau để tính toán.
Cách giải:
Gọi số sản phẩm mà tổ I, tổ II, tổ III đăng kí sản xuất là z,y,z (sản phẩm) (điều kiện: z,y,z∈N)
Vì ba tổ đăng kí sản xuất tổng số 270 sản phẩm nên x+y+z=270
Vì số sản phẩm của mỗi tổ sản xuất được tỉ lệ thuận với số người của tổ nên ta có: x10=y8=z9
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: x10=y8=z9=x+y+z10+8+9=27027=10
Khi đó, x10=10⇒x=100 (sản phẩm)
y8=10⇒y=80 (sản phẩm)
z9=10⇒z=90 (sản phẩm)
Vậy số sản phẩm mà mỗi tổ đăng kí sản xuất là: tổ I: 100 sản phẩm, tổ II: 80 sản phẩm, tổ III: 90 sản phẩm.
Bài 4
Phương pháp:
+ Nếu một đường thẳng cắt hai đường thẳng song song thì:
* Cặp góc đồng vị bằng nhau
* Cặp góc so le trong bằng nhau.
* Cặp góc trong cùng phía bù nhau
Cách giải:
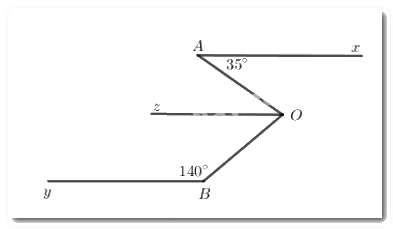
Kẻ Oz//Ax//By
Vì Ax//Oz nên ∠xAO=∠zOA=35∘ (hai góc so le trong)
Vì Oz//By nên ∠yBO+∠zOB=180∘ (hai góc trong cùng phía)
140∘+∠zOB=180∘
⇒∠zOB=180∘−140∘=40∘
Ta có: ∠AOB=∠zOA+∠zOB=35∘+40∘=75∘
Bài 5
Phương pháp:
Vận dụng kiến thức về dấu giá trị tuyệt đối: |A(x)|≥0 với mọi số thực x.
Cách giải:
Do |x|≥0;|x+2|≥0 với mọi số thực x nên |x|+|x+2|≥0 với mọi số thực x.
Do đó, |x|+|x+2|=0 khi |x|=0 và |x+2|=0.
Suy ra x đồng thời bằng 0 và bằng −2 (vô lí).
Vậy không có giá trị nào của x thỏa mãn yêu cầu của đề bài.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365