Đừng bỏ lỡ những tính năng hấp dẫn của Baitap365.com
Đề thi học kì 1 Toán 7 Cánh diều
Đề thi học kì 1 Toán 7 - Đề số 2 - Cánh diều
Đề thi học kì 1 Toán 7 - Đề số 3 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 4 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 5 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 6 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 7 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 8 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 9 - Cánh diều Đề thi học kì 1 Toán 7 - Đề số 10 - Cánh diều Đề thi học kì 1 Toán 7 Cánh diều - Đề số 11 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 12 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 13 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 14 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 15 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 16 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 17 Đề thi học kì 1 Toán 7 Cánh diều - Đề số 18 Đề thi học kì 1 Toán 7 - Đề số 1 - Cánh diều Đề cương ôn tập học kì 1 Toán 7 - Cánh diềuĐề thi học kì 1 Toán 7 - Đề số 2 - Cánh diều
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Số đối của −712 là:
A. 712
B. 7−12
C. 12−7
D. 127
Câu 2: Chọn khẳng định đúng.
A. −3741>23−17
B. (13)12>(13)10
C. (2,5)6=(0,5)12
D. (2,5)4<(−2,5)5
Câu 3: Chọn đáp án sai. Nếu √x=23 thì:
A. x=(−23)2
B. x=−(−23)2
C. x=49
D. x=(23)2
Câu 4: Trong các phát biểu sau, phát biểu nào sai?
A. Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.
B. Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
C. Hai số đối nhau có giá trị tuyệt đối bằng nhau.
D. Giá trị tuyệt đối của một số thực luôn bằng chính nó.
Câu 5: Các tỉ số nào sau đây lập thành một tỉ lệ thức?
A. 712 và 56;43
B. 1521 và 135175
C. −13 và −1957
D. 67;145 và 73;29
Câu 6: Với số tiền mua được 96 kg gạo có thể mua được bao nhiêu ki – lô – gam ngô, biết rằng giá 1 kg ngô chỉ bằng 48% giá của 1 kg gạo?
A. 120 kg
B. 160 kg
C. 200 kg
D. 240 kg
Câu 7: Một khối gỗ dạng hình hộp chữ nhật có kịch thước như Hình a). Người ta cắt đi một phần khối gỗ có dạng hình lập phương cạnh 5 cm. Tính thể tích phần còn lại của khối gỗ (Hình b).
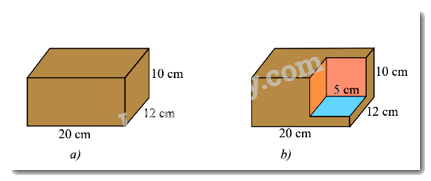
A. 1888cm3
B. 2275cm3
C. 2144cm3
D. 2300cm3
Câu 8: Trong các hình sau, hình nào là hình lăng trụ đứng tứ giác?
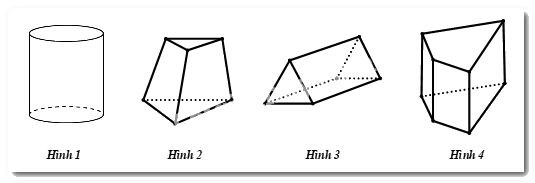
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Câu 9: Phát biểu định lí sau bằng lời:
|
GT |
a//b,c⊥a |
|
KL |
c⊥b |
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc 600.
D. Cả A, B, C đều đúng.
Câu 10: Vẽ ∠xOy=500. Vẽ tia Om là tia phân giác của góc xOy. Vẽ tia On là tia đối của tia Ox. Tính góc mOn.
A. ∠mOn=1250
B. ∠mOn=1550
C. ∠mOn=1600
D. ∠mOn=1750
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) 29+13:(−32)+12.(−0,5)0
b) (−12)2−58:(0,5)3−53.(−6)
c) √0,04+√0,25+2,31
d) |√169−√900|−|−54|:(13−12)2
Bài 2: (2,0 điểm)
Tìm x, biết:
a) 13x+25(x−1)=0
b) (2x+1)2=3625
c) 12x+√0,04=√1,96
d) ||2x−1|+12|=45
Bài 3: (1,5 điểm)
Bốn cuộn dây điện cùng loại có tổng khối lượng là 26 kg.
a) Tính khối lượng từng cuộn, biết cuộn thứ nhất nặng bằng 12 cuộn thứ hai, bằng 14 cuộn thứ ba và bằng 16 cuộn thứ tư.
b) Biết cuộn thứ nhất dài 100 m, hãy tính xem một mét dây điện nặng bao nhiêu gam?
Bài 4: (1,0 điểm)
Một chiếc bánh ngọt có dạng hình lăng trụ đứng tam giác, có kích thước như hình vẽ bên dưới.
a) Tính thể tích cái bánh.
b) Nếu phải làm một chiếc hộp để đựng vừa khít cái bánh này thì chi phí làm hộp là bao nhiêu biết giá 1 mét vuông bìa là 22500 đồng.
Bài 5: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức A=x2+√x−113 với x≥0.
Lời giải
Phần I: Trắc nghiệm:
|
1.A |
2.A |
3.B |
4.D |
5.C |
6.C |
7.B |
8.D |
10.B |
Câu 1
Phương pháp:
Số đối của số hữu tỉ a kí hiệu là −a.
Cách giải:
Số đối của −712 là: −(−712)=712
Chọn A.
Câu 2
Phương pháp:
Sử dụng phương pháp so sánh trung gian.
Cách giải:
+ Ta có: 37<41 nên 3741<1 suy ra −3741>−1 (1)
23>17 nên 2317>1 suy ra 23−17<−1 (2)
Từ (1) và (2), suy ra 23−17<−1<−3741, do đó, −3741>23−17
Vậy đáp án A đúng.
Chọn A.
Câu 3
Phương pháp:
Căn bậc hai số học của số a không âm là số x không âm sao cho x2=a.
Sử dụng tính chất: x2=(−x)2
Cách giải:
√(−23)2=√(23)2=√49=23 nên đáp án A,C,D đúng
Do chỉ tồn tại căn bậc hai số học của một số không âm nên đáp án B sai.
Chọn B.
Câu 4
Phương pháp:
Vận dụng kiến thức giá trị tuyệt đối của một số thực, tìm phát biểu sai.
Cách giải:
Phát biểu A đúng vì giá trị tuyệt đối của một số thực là một số không âm.
Phát biểu B đúng vì hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
Phát biểu C đúng vì hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên giá trị tuyệt đối của chúng bằng nhau.
Phát biểu D sai vì giá trị tuyệt đối của số âm là số đối của nó.
Chọn D.
Câu 5
Phương pháp:
Tỉ lệ thức là đẳng thức của hai tỉ số ab và cd, viết là ab=cd.
Cách giải:
+ Cặp tỉ số: 712 và 56;43
Ta có: 56=1012;43=1612
Vì 712≠1012≠1612 nên 712≠56≠43 do đó cặp tỉ số 712 và 56;43 không lập thành một tỉ lệ thức, loại đáp án A.
+ Cặp tỉ số: 1521 và 135175
Ta có: 1521=57=2535;135175=2735
Vì 2535≠2735 nên 1521≠135175 do đó cặp tỉ số 1521 và 135175 không lập thành một tỉ lệ thức, loại đáp án B.
+ Cặp tỉ số: −13 và −1957
Ta có: −1957=−13
Vì hai tỉ số đã cho đều bằng −13 nên cặp tỉ số −13 và −1957 lập thành một tỉ lệ thức, chọn đáp án C.
Chọn C.
Câu 6
Phương pháp:
Gọi khối lượng ngô có thể mua được là x (kg)
Xác định hai đại lượng tỉ lệ nghịch, lập tỉ lệ thức.
Áp dụng tính chất của dãy tỉ số bằng nhau, tìm x.
Cách giải:
Gọi khối lượng ngô có thể mua được là x (kg)
Vì với cùng một số tiền thì khối lượng mua được và giá của loại hàng đó là hai đại lượng tỉ lệ nghịch nên ta có:
x96=giá1kggạogiá1kgngô=100%48%=10048=2512
Suy ra x=96.2512=200 (kg)
Vậy với số tiền mua được 96 kg gạo có thể mua được 200 kg ngô.
Chọn C.
Câu 7
Phương pháp:
Thể tích của hình hộp chữ nhật có chiều dài đáy là a, chiều rộng đáy là b và chiều cao là c:V=abc
Thể tích của hình lập phương có một cạnh là a:V=a3
Cách giải:
Thể tích ban đầu của khối gỗ là: V1=20.12.10=2400(cm3)
Thể tích phần khối gỗ cắt bỏ đi là: V2=53=125(cm3)
Thể tích phần còn lại của khối gỗ là: V=V1−V2=2400−125=2275(cm3)
Chọn B.
Câu 8
Phương pháp:
Hình lăng trụ đứng tứ giác là hình có hai mặt đáy cùng là tứ giác và song song với nhau; các mặt bên đều là hình chữ nhật; các cạnh bên bằng nhau.
Cách giải:
Trong 4 hình vẽ, ta nhận thấy Hình 4 là hình lăng trụ đứng tứ giác.
Chọn D.
Câu 9
Phương pháp:
Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
Cách giải:
Phát biểu định lí: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Chọn A.
Câu 10
Phương pháp
Oz là tia phân giác của ∠xOy thì ta có: ∠xOz=∠zOy=∠xOy2
∠xOz và ∠zOy là hai góc kề nhau thì ta có: ∠xOz+∠zOy=∠xOy.
∠xOz và ∠zOy là hai góc kề bù thì ta có: ∠xOy=∠xOz+∠zOy=1800
Cách giải:
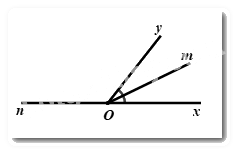
Vì Om là tia phân giác của ∠xOy nên ∠mOy=∠xOy2=5002=250
Ta có: ∠nOy và ∠yOx là hai góc kề bù nên ∠nOy+∠yOx=1800
⇒∠nOy+500=1800⇒∠nOy=1800−500=1300
Ta có: ∠nOy và ∠yOm là hai góc kề nhau nên ∠nOy+∠yOm=∠nOm
⇒1300+250=1550=∠nOm
Vậy ∠mOn=1550
Chọn B.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
a) Đổi số thập phân sang phân số
Thực hiện các phép toán với số hữu tỉ.
b) Lũy thừa của một số hữu tỉ: (ab)n=anbn(b≠0;n∈Z)
Thực hiện các phép toán với số hữu tỉ.
c) Tính căn bậc hai số học của một số thực
Thực hiện các phép toán với số hữu tỉ.
d) Lũy thừa của một số hữu tỉ: (ab)n=anbn(b≠0;n∈Z)
Tính căn bậc hai số học của một số thực
Vận dụng kiến thức giá trị tuyệt đối của một số thực: |x|={xkhix>0−xkhix<00khix=0
Thực hiện các phép toán với số hữu tỉ.
Cách giải:
a) 29+13:(−32)+12.(−0,5)0
=29+13.(−23)+12.1=29+−29+12=0+12=12
b) (−12)2−58:(0,5)3−53.(−6)
=(−1)222−58:(12)3−5.(−2)=14−58:1323−(−10)=14−58:18+10=14−58.81+10=14−5+10=14+5=14+204=214
c) √0,04+√0,25+2,31
=√(0,2)2+√(0,5)2+2,31=0,2+0,5+2,31=3,01
d) |√169−√900|−|−54|:(13−12)2
=|√132−√302|−54:(26−36)2=|13−30|−54:(16)2=|−17|−54:136=17−54.36=17−45=−28
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm x.
b) Giải [A(x)]2=a2=(−a)2
Trường hợp 1: A(x)=a
Trường hợp 2: A(x)=−a
c) Tính căn bậc hai số học của số thực
Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm x.
d) |x|=a
Trường hợp a<0, khi đó phương trình không có nghiệm x
Trường hợp a>0, vận dụng kiến thức giá trị tuyệt đối của một số thực: |x|={xkhix>0−xkhix<00khix=0
Cách giải:
a) 13x+25(x−1)=0
13x+25x−25=0x.(13+25)=25x.(515+615)=25x.1115=25x=25:1115x=25.1511x=611
Vậy x=611
b) (2x+1)2=3625
(2x+1)2=(65)2=(−65)2
Trường hợp 1:
2x+1=652x=65−1=65−552x=15x=15:2=15.12x=110
Vậy x∈{110;−1110}
Trường hợp 2:
2x+1=−652x=−65−1=−65−552x=−115x=−115:2=−115.12x=−1110
c) 12x+√0,04=√1,96
12x+√(0,2)2=√(1,4)212x+0,2=1,412x=1,4−0,2=1,2x=1,2:12=1,2.2x=2,4
Vậy x=2,4.
d) ||2x−1|+12|=45
Trường hợp 1:
|2x−1|+12=45|2x−1|=45−12=810−510|2x−1|=310
*2x−1=310
2x=310+1=310+10102x=1310x=1310:2=1310.12x=1320
*2x−1=−310
2x=−310+1=−310+10102x=710x=710:2=710.12x=720
Trường hợp 2:
|2x−1|+12=−45|2x−1|=−45−12=−810−510|2x−1|=−1310
Vì −1310<0 nên không có x thỏa mãn |2x−1|=−1310.
Vậy x∈{1320;720}
Bài 3
Phương pháp:
a) Gọi khối lượng của cuộn dây thứ nhất, thứ hai, thứ ba và thứ tư lần lượt là x,y,z,t (kg) (điều kiện: x,y,z,t>0)
Xác định hai đại lượng tỉ lệ thuận, lập tỉ lệ thức.
Áp dụng tính chất của dãy tỉ số bằng nhau, tìm x,y,z,t
b) Thực hiện phép chia, tính được số gam của một mét dây điện.
Cách giải:
a) Gọi khối lượng của cuộn dây thứ nhất, thứ hai, thứ ba và thứ tư lần lượt là x,y,z,t (kg) (điều kiện: x,y,z,t>0)
Do khối lượng và chiều dài của mỗi cuộn dây là hai đại lượng tỉ lệ thuận nên x1=y2=z4=t6
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x1=y2=z4=t6=x+y+z+t1+2+4+6=2613=2
Do đó, x1=2 suy ra x=1.2=2(tm)
y2=2 suy ra y=2.2=4(tm)
z4=2 suy ra z=4.2=8(tm)
t6=2 suy ra t=6.2=12(tm)
Vậy khối lượng của cuộn dây thứ nhất, thứ hai, thứ ba và thứ tư lần lượt là 2 kg, 4 kg, 8 kg và 12 kg.
b) Ta có: 2:100=0,02 (kg) =20 (gam)
Vậy một mét dây điện nặng 20 gam.
Bài 4
Phương pháp:
a) Thể tích của hình lăng trụ đứng tam giác: V=Sđáy.h
Trong đó: V: thể tích của hình lăng trụ đứng tam giác
Sđáy: diện tích một đáy của hình lăng trụ đứng tam giác
h: chiều cao của hình lăng trụ đứng tam giác
b) Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: Sxq=Cđáy.h
Trong đó: Sxq: diện tích xung quanh hình lăng trụ đứng tam giác
Cđáy: diện tích một đáy của hình lăng trụ đứng tam giác
h: chiều cao của hình lăng trụ đứng tam giác
Chi phí làm hộp = (diện tích xung quanh + diện tích hai đáy) . giá tiền 1 mét vuông bìa
Cách giải:
a) Đáy của hình lăng trụ tam giác là một tam giác vuông nên diện tích đáy là: Sđáy=12.9.12=54(cm2)
Thể tích cái bánh là: V=Sđáy.h=54.5=270(cm3)
b) Chu vi đáy của cái bánh là: C=9+12+15=36(cm)
Diện tích xung quanh của cái bánh là: Sxq=C.h=36.5=180(cm2)
Diện tích hai đáy của cái bánh là: S=2.54=108(cm2)
Diện tích làm hộp của cái bánh là: Sxq+S=180+108=288(cm2)=0,0288(m2)
Chi phí làm hộp là: 0,0288.22500=648 (đồng)
Bài 5
Phương pháp:
Đánh giá các số hạng của tổng để tìm giá trị nhỏ nhất của A.
Chú ý: x2≥0,∀x∈R.
Cách giải:
Ta có: x2≥0;√x≥0 với mọi số thực x≥0 nên x2+√x≥0 với mọi số thực x≥0.
Suy ra x2+√x−113≥−113 với mọi số thực x≥0. Hay A≥−113 với mọi số thực x≥0.
Dấu “=” xảy ra ⇔x=0.
Vậy min.
Mẹo tìm đáp án nhanh
Search Google: "từ khóa + baitap365" Ví dụ: "Bài 5 trang 13 SGK Vật lí 12 baitap365